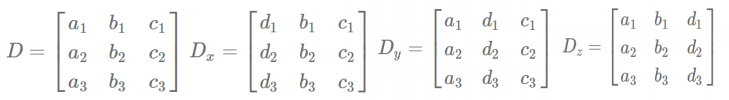CAT Linear Equations : Important Concepts and Notes PDF
What is a Linear Equation?
A linear equation is an equation which gives straight line when plotted on a graph.
- Linear equations can be of one variable or two variables or three variables.
- Let a, b, c and d are constants and x, y and z are variables. A general form of a single variable linear equation is ax+b = 0.
- A general form of two variable linear equation is ax+by = c.
- A general form of three variable linear equation is ax+by+cz = d.

Linear Equations in Two Variables
- Linear equations in two variables is an equation of the form ax + by + c = 0, where x and y are the two variables and a, b, and c are real numbers and a and b are non-zero.
- It is popularly known as a simultaneous linear equation.
- Linear equations in two variables are usually used in geometry to find the coordinates of a straight line.
Forms of Linear Equations in Two Variables
Linear equations in two variables are sorts of equations with a unique solution, no solutions, or infinitely many solutions. They can be present in different forms:
- Standard form
- Intercept form
- Point-slope form

1. Standard Form of Linear Equations in Two Variables
- The format of the equation representation in standard form is ax + by + c = 0
- Here a, b and c are the coefficient constants.
- Consider an equation as 3x + 4y = 11. In standard form the equation is represented as:
3x + 4y - 11 = 0
2. Intercept Form of Linear Equations in Two Variables
- The format of the equation representation in intercept form is: y = mx + b
- In the above equation, m is the slope and b stands for the y-intercept.
- Consider the same equation as 3x + 4y = 11. In the intercept or say slope-intercept form for the equation is represented as:
y = (-3/4)x + 11/4
3. Point Slope Form of Linear Equations in Two Variables
- The format of the equation representation in point-slope form is: y − y1 = m(x − x1)
- Where m=slope and (x1, y1) denotes a point on the given line.
- An example of the point-slope form is: y - 4 = 5(x - 3)
Here 5 is the slope and (3, 4) denotes a point on the given line.
System of Simultaneous Linear Equations in Two Variables
Let us consider two linear equations in two variables,
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
These two equations are said to form a system of simultaneous linear equations or simply a pair of linear equations.
Example: x + y − 3 = 0
2x − 5y + 1 = 0
Is a pair or a system of two simultaneous linear equations in two variables x and y.
Sol: A solution to a pair of linear equations in two variables is an ordered pair of numbers that satisfy both equations.
For the above example, x = 2, y = 1 is a solution to the pair of linear equations. We can verify this by substituting x = 2, y = 1 into each of these two equations.
The graphical representation of a pair of linear equations in two variables is always given by two straight lines which are intersecting lines or parallel lines or coincident lines.
Nature of Solution of Linear Equations in Two Variables
- A system of linear equations in two variables can have one solution or no solution or infinitely many solutions.
- A system of linear equations is consistent if it has a solution, meaning that there is at least one set of values that satisfies all the equations. On the other hand, an inconsistent system does not have a solution, indicating that no set of values can satisfy all the equations simultaneously.
- Similarly, a system of linear equations is considered independent if it has a unique solution, meaning that the values of the variables can be determined uniquely. In contrast, a dependent system has an infinite number of solutions.
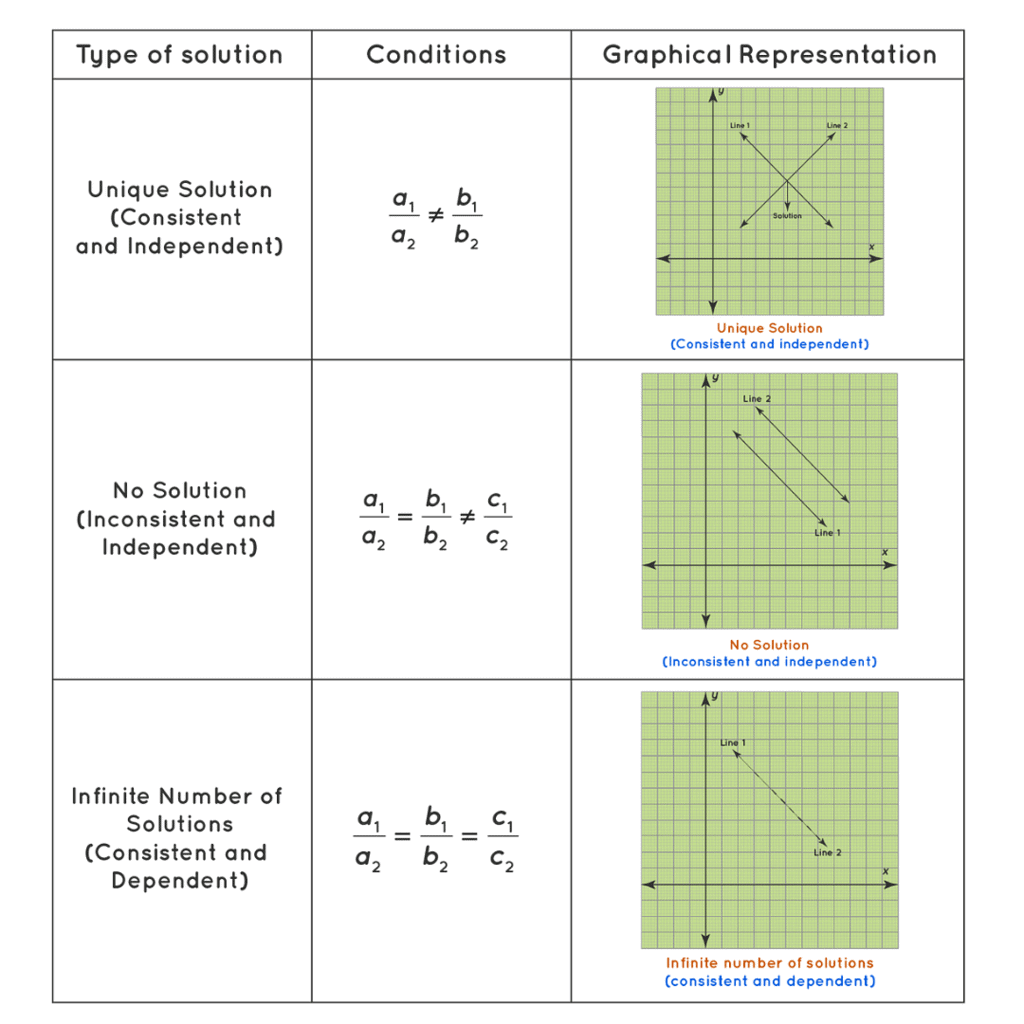
1. Unique Solution of Linear Equations in Two Variables
- A system of linear equations in two variables has a unique solution if and only if the equations represent two non-parallel lines that intersect at exactly one point. In other words, the lines must have different slopes, indicating that they are not parallel, and they must intersect at one point only.
- Therefore, if m1 and m2 are the slopes of the equations of the two lines, then m1 should not be equal to m2 in order for the equations to have a unique solution, that is, m1 ≠ m2.
- The unique solution can be found by solving the equations simultaneously using various methods, including substitution, elimination, or matrices. It is important to note that a system of linear equations may have zero solutions or infinitely many solutions if the lines are parallel or coincide with each other.
2. No Solution of Linear Equations in Two Variables
- A system of linear equations in two variables has no solution if and only if the equations represent two parallel lines that do not intersect. In other words, the lines must have the same slope, indicating that they are parallel, and they do not intersect.
- This can be represented mathematically as m1 = m2, where m1 and m2 are the slopes of the lines.
- When a system of linear equations has no solution, it means that there is no value for each variable that satisfies both equations simultaneously. This situation is often called an inconsistent system, and it arises when the lines represented by the equations do not cross each other.
3. Infinite Solutions of Linear Equations in Two Variables
- It is important to note that a system of linear equations may have infinitely many solutions if the equations represent the same line or coincident lines.
- In such a case on of the linear equation is a scalar multiple of the other equation, like in the case of x + y =2 and 2x + 2y = 4.
How to Solve Linear Equations in Two Variables
The various methods to solve linear equations in two variables are given below:
- Substitution Method
- Elimination Method
- Cross-multiplication method
- Graphical Method
- Determinant Method
1. Substitution Method to Solve Linear Equations in Two Variables
Procedure of Substitution Method to Solve Linear Equations in Two Variables is as follows:
Step 1. Solve one of the given equations to get the value of one of the variables in terms of the other, whichever is convenient.
Step 2. Substitute the value of the variable so obtained in the other equation.
Step 3. Solve the resulting single variable equation. Now substitute this value into either of the two original equations and solve it to find the value of the second variable.
Example 1. Solve the following system of linear equations:
4x-3y=8
x-2y= -3
Sol: The given equations are
4x-3y=8 ……….(i)
x-2y= -3 ……….(ii)
We can solve either equation for either variable. But to avoid fractions, we solve the second equation for x,
x=2y-3 ……….(iii)
Substituting this value of x in equation (i), we get
4(2y-3)-3y=8
8y-12-3y=8
5y=20
y=4.
Substituting this value of y in (ii), we get
x-24= -3
x-8= -3
x=5.
Hence, the solution is x = 5, y = 4.
Example 2. Solve the following system of linear equations:
8x+5y=9
3x+2y=4.
Sol: The given equations are
8x+5y=9 ……….(i)
3x+2y=4 ……….(ii)
From equation (ii), we get
2y = 4−3xy
Substituting this value of y in (i), we get
Substituting this value of x in equation (ii), we get
3(-2) + 2y = 4
2y = 10
y = 5.
Hence, the solution is x = -2, y = 5.
2. Elimination Method to Solve Linear Equations in Two Variables
This method uses the elimination of any one variable. This method is usually more convenient than the substitution method. An easy method to solve equations using elimination method is that if the coefficient of either x or y is 1 in any one of the equations, then multiply both sides of that equation by the coefficient of the same variable in the second equation. Further, add or subtract (according to the sign) to eliminate that variable.
Procedure of Elimination Method to Solve Linear Equations in Two Variables:
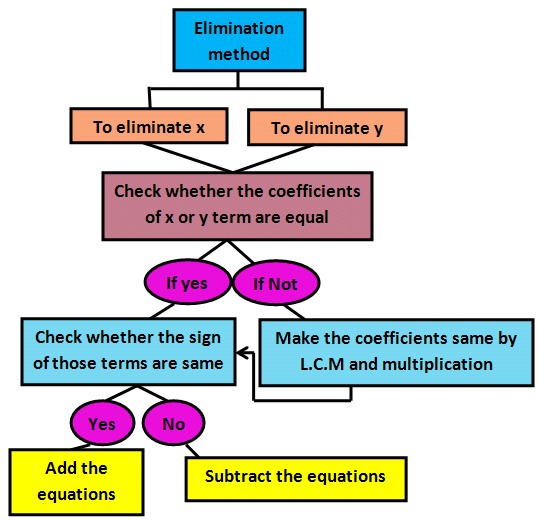 Step 1. Multiply one or both equations (if necessary) by a suitable number(s) in a way that addition or subtraction will eliminate one variable.
Step 1. Multiply one or both equations (if necessary) by a suitable number(s) in a way that addition or subtraction will eliminate one variable.
Step 2. Solve the resulting single variable equation to find the value of this variable. Now substitute this value into either of the two original equations and solve it to find the value of the variable that was earlier eliminated.
3. Cross-Multiplication Method to Solve Linear Equations in Two Variables
Procedure of Cross-Multiplication Method to Solve Linear Equations in Two Variables:
Let the system of simultaneous linear equations be
a1x + b1y + c1=0
a2x + b2y + c2 = 0
To solve this system of linear equations by cross-multiplication method, the solution is given by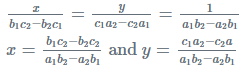
4. Graphical Method to Solve Linear Equations in Two Variables
The next method to solve linear equations in two variables is the graphical approach. To decode two linear equations in two variables graphically we will follow the below steps:
- Step 1: We will start with graphing the two equations on the graph.
- Step 2: To plot the graph manually, transform the equations to the form y = mx + b or x = my +b.
- Step 3: Substitute the different values of x like 0, 1, 2,…… and obtain the related values of y, or vice-versa to obtain different values of x.
- Step 4: Plot the different points of the equation on the graph and try to locate the point where both lines intersect one another.
- Step 5: The point of the meeting is the answer to the given system of equations.
It is not always possible that both the lines will intersect one another, they can even be parallel or coincide with each other. In such a case we can follow the below conclusions:
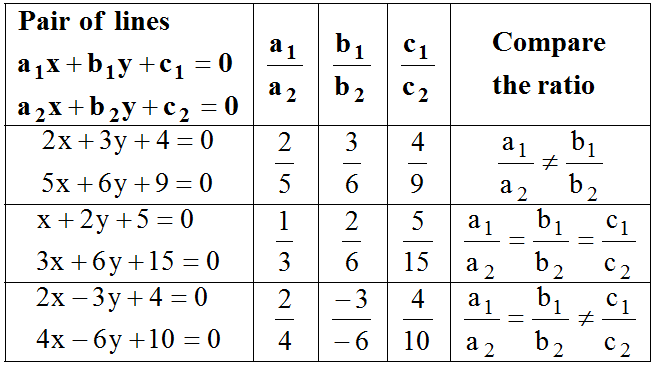
- If we are given a system of two linear equations: a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0
- If a1/a2 ≠ b1/b2
- In such a case a unique solution is obtained also the given set of lines intersects at a single point.
- If a1/a2 = b1/b2 ≠ c1/c2
- In such a case the system equations have no solution also the lines are parallel to one another.
- a1/a2 = b1/b2 = c1/c2
- For the above case, the system equations have an infinite number of solutions and the given two lines coincide with each other. If the system holds a solution, then it is stated to be consistent; otherwise, it is considered inconsistent.
5. Determinant Method to Solve Linear Equations in Two Variables
Under this method, we will learn to determine the solution for a system of linear equations in two variables. The steps are as follows:
Step 1: Consider the questions as: a1x + b1y = c1 and a2x + b2y = c2
Step 2: We would first locate the determinant developed by the coefficients of x and y and mark it as Δ.
Step 3: Next we will obtain the determinant Δx which is the determinant calculated by replacing the first column of Δ with the constant terms in the equation.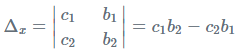
Step 4: Similarly we will determine the determinant Δy which is calculated by replacing the second column of Δ with the constant terms in the equation.
Step 5: Lastly the solution for the provided system of linear equations is received by the formulas:
Equations with Three Variables
- Let the equations be a1x + b1y + c1z = d1, a2x+b2y+c2z = d2 and a3x+b3y+c3z = d3 . Here we define the following matrices:

- If Determinant of D ≠ 0, then the equations have a unique solution.
- If Determinant of D = 0, and at least one but not all of the determinants Dx , Dy or Dz is zero, then no solution exists.
- If Determinant of D = 0, and all the three of the determinants Dx , Dy and Dz are zero, then there are infinitely many solution exists.
- Determinant can be calculated by D = a1(b2c3 -c2b3) - b1(a2c3 - c2a3) + c1(a2b3 -b2a3)
Solving Equations with Three Variables
Step 1. Take any two equation out given three equation, and solve it for one variable.
Again take two equation and solve it for same variable as above.
Now solve the two equation so form. and find their value, and put the value in any of the three equation.
For example,
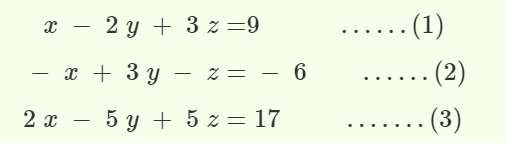
Step 2. Add equation (1) and (2) to eliminate x
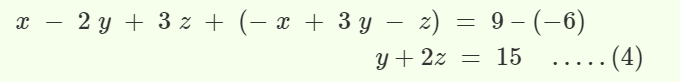
Step 3. Solve, equation 1 and 3, by multiplying equation (1) with -2 and adding to equation (3)
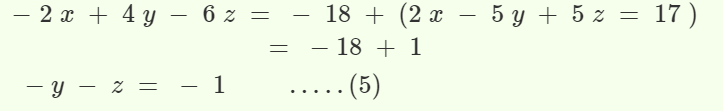
Step 4. Solve for equation 4 and 5

z= 2
x= 1
y= -1
Therefore, the solution for the given three equations is (1, -1, 2)
Hence, in this way we can solve linear equation in three variable.
Solved Examples
Q1: For some real numbers a and b, the system of equations  has infinitely many solutions for x and y. Then, the maximum possible value of ab is:
has infinitely many solutions for x and y. Then, the maximum possible value of ab is:
(a) 33
(b) 25
(c) 15
(d) 55
Ans: (a)
Sol: It is given that for some real numbers a and b, the system of equations 
8b has infinitely many solutions for x and y.
Hence, we can say that 
This equation can be used to find the value of a, and b.
Firstly, we will determine the value of b.

Hence, the values of b are 5, and -3, respectively.
The value of a can be expressed in terms of b, which is

The correct option is A.
Q2: Three friends, returning from a movie, stopped to eat at a restaurant. After dinner, they paid their bill and noticed a bowl of mints at the front counter. Sita took one-third of the mints, but returned four because she had a momentary pang of guilt. Fatima then took one-fourth of what was left but returned three for similar reason. Eswari then took half of the remainder but threw two back into the bowl. The bowl had only 17 mints left when the raid was over. How many mints were originally in the bowl?
(a) 38
(b) 31
(c) 41
(d) None of these
Answer (D)
Solution:
Let the total number of mints in the bowl be n
Sita took n/3 – 4. Remaining = 2n/3 + 4
Fatim took 1/4(2n/3 + 4) – 3. Remaining = 3/4(2n/3 + 4) + 3
Eswari took 1/2(3/4(2n/3+4)+3) – 2
Remaining = 1/2(3/4(2n/3+4)+3) + 2 = 17
=> 3/4(2n/3+4)+3 = 30 => (2n/3+4) = 36 => n = 48
So, the answer is option d)
Q3: In 2010, a library contained a total of 11500 books in two categories – fiction and nonfiction. In 2015, the library contained a total of 12760 books in these two categories. During this period, there was 10% increase in the fiction category while there was 12% increase in the non-fiction category. How many fiction books were in the library in 2015?
(a) 6160
(b) 6600
(c) 6000
(d) 5500
Answer (B)
Solution:
Let the number of fiction and non-fiction books in 2010 = 100a, 100b respectively
It is given that the total number of books in 2010 = 11500
100a+100b = 11500 ——-Eq 1
The number of fiction and non-fiction books in 2015 = 110a, 112b respectively
110a+112b = 12760 ——-Eq 2
On solving both the equations we get, b=55, a= 60
The number of fiction books in 2015 = 110*60=6600
|
154 videos|396 docs|723 tests
|
FAQs on CAT Linear Equations : Important Concepts and Notes PDF
| 1. What is a linear equation and how is it defined? |  |
| 2. How can I represent a system of simultaneous linear equations in two variables? |  |
| 3. What are the possible nature of solutions for linear equations in two variables? |  |
| 4. What methods can I use to solve linear equations in two variables? |  |
| 5. How do equations with three variables differ from those with two variables? |  |
|
154 videos|396 docs|723 tests
|

|
Explore Courses for CUET Commerce exam
|

|