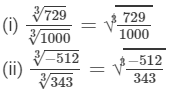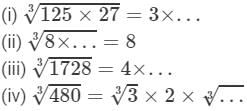RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-4) | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1: Find the cube roots of each of the following integers:
(i) −125
(ii) −5832
(iii) −2744000
(iv) −753571
(v) −32768
Answer 1: (i) We have:
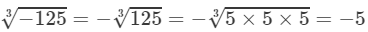
(ii) We have:
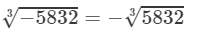
To find the cube root of 5832, we use the method of unit digits.
Let us consider the number 5832.
The unit digit is 2; therefore the unit digit in the cube root of 5832 will be 8.
After striking out the units, tens and hundreds digits of the given number, we are left with 5.
Now, 1 is the largest number whose cube is less than or equal to 5.
Therefore, the tens digit of the cube root of 5832 is 1.
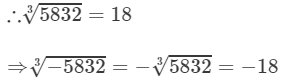
(iii) We have:
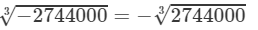
To find the cube root of 2744000, we use the method of factorisation.
On factorising 2744000 into prime factors, we get:
2744000=2×2×2×2×2×2×5×5×5×7×7×72744000=2×2×2×2×2×2×5×5×5×7×7×7
On grouping the factors in triples of equal factors, we get:
2744000={2×2×2}×{2×2×2}×{5×5×5}×{7×7×7}2744000=2×2×2×2×2×2×5×5×5×7×7×7
It is evident that the prime factors of 2744000 can be grouped into triples of equal factors and no factor is left over.
Now, collect one factor from each triplet and multiply; we get:
2×2×5×7=1402×2×5×7=140
This implies that 2744000 is a cube of 140.
Hence, 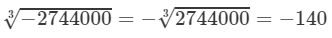
(iv) We have:
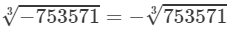
To find the cube root of 753571, we use the method of unit digits.
Let us consider the number 753571.
The unit digit is 1; therefore the unit digit in the cube root of 753571 will be 1.
After striking out the units, tens and hundreds digits of the given number, we are left with 753.
Now, 9 is the largest number whose cube is less than or equal to 753 (93<753<10393<753<103).
Therefore, the tens digit of the cube root 753571 is 9.
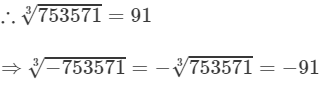
(v) We have:
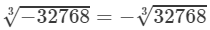
To find the cube root of 32768, we use the method of unit digits.
Let us consider the number 32768.
The unit digit is 8; therefore, the unit digit in the cube root of 32768 will be 2.
After striking out the units, tens and hundreds digits of the given number, we are left with 32.
Now, 3 is the largest number whose cube is less than or equal to 32 (33<32<4333<32<43).
Therefore, the tens digit of the cube root 32768 is 3.
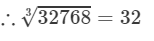
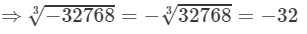
Question 2: Show that:
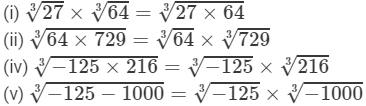
Answer 2:
(i) LHS = 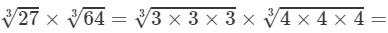 3×4=12273×643=3×3×33×4×4×43=3×4=12
3×4=12273×643=3×3×33×4×4×43=3×4=12
RHS = 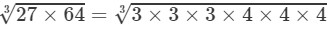
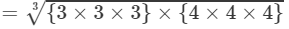
=3×4=1227×643=3×3×3×4×4×43=3×3×3×4×4×43=3×4=12
Because LHS is equal to RHS, the equation is true.
(ii) LHS = 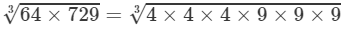
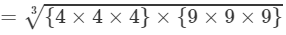 =4×9=3664×7293=4×4×4×9×9×93=4×4×4×9×9×93=4×9=36
=4×9=3664×7293=4×4×4×9×9×93=4×4×4×9×9×93=4×9=36
RHS = 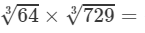
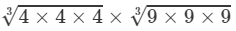 =4×9=36
=4×9=36
Because LHS is equal to RHS, the equation is true.
(iii) LHS =
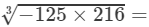
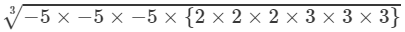 =
=
=−5×2×3=−30
RHS =
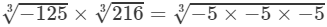
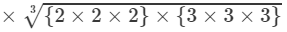 =−5×(2×3)=−30
=−5×(2×3)=−30
Because LHS is equal to RHS, the equation is true.
(iv) LHS =
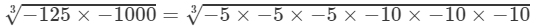
−5×−10=50
RHS = 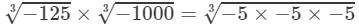
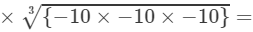
=−5×−10=50-1253×-10003=-5×-5×-53×-10×-10×-103=-5×-10=50
Because LHS is equal to RHS, the equation is true.
Question 3: Find the cube root of each of the following numbers:
(i) 8 × 125
(ii) −1728 × 216
(iii) −27 × 2744
(iv) −729 × −15625
Answer 3: Property:
For any two integers a and b, 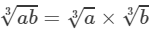
(i) From the above property, we have:
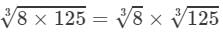
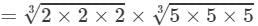 =2×5=10
=2×5=10
(ii) From the above property, we have:
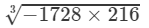
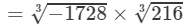
 (For any positive integer x,
(For any positive integer x, 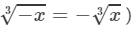
Cube root using units digit:
Let us consider the number 1728.
The unit digit is 8; therefore, the unit digit in the cube root of 1728 will be 2.
After striking out the units, tens and hundreds digits of the given number, we are left with 1.
Now, 1 is the largest number whose cube is less than or equal to 1.
Therefore, the tens digit of the cube root of 1728 is 1.
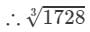 =12
=12
On factorising 216 into prime factors, we get:
216=2×2×2×3×3×3216=2×2×2×3×3×3
On grouping the factors in triples of equal factors, we get:
216={2×2×2}×{3×3×3}216=2×2×2×3×3×3
Now, taking one factor from each triple, we get:
 = 2×3 = 6
= 2×3 = 6
Thus
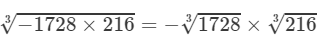 =−12×6=−72
=−12×6=−72
(iii) From the above property, we have:
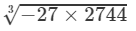
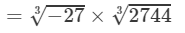
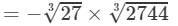 (For any positive integer x,
(For any positive integer x, 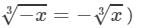
Cube root using units digit:
Let us consider the number 2744.
The unit digit is 4; therefore, the unit digit in the cube root of 2744 will be 4.
After striking out the units, tens, and hundreds digits of the given number, we are left with 2.
Now, 1 is the largest number whose cube is less than or equal to 2.
Therefore, the tens digit of the cube root of 2744 is 1.
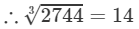
Thus
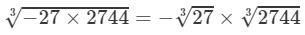 =−3×14=−42
=−3×14=−42
(iv) From the above property, we have:

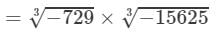
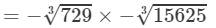 (For any positive integer x,
(For any positive integer x, 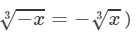
Cube root using units digit:
Let us consider the number 15625.
The unit digit is 5; therefore, the unit digit in the cube root of 15625 will be 5.
After striking out the units, tens and hundreds digits of the given number, we are left with 15.
Now, 2 is the largest number whose cube is less than or equal to 15 ((23<15<33)23<15<33.
Therefore, the tens digit of the cube root of 15625 is 2.
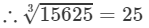
Also
 9, because 9×9×9=729
9, because 9×9×9=729
Thus
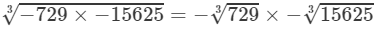 =−9×−25=225
=−9×−25=225
Question 4: Evaluate:
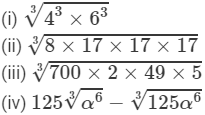
Answer 4:Property:
For any two integers a and b, 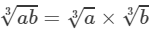
(i) From the above property, we have:
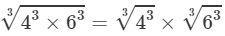 =4×6=24
=4×6=24
(ii) Use above property and proceed as follows:
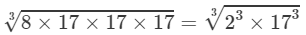
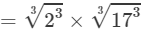 =2×17=34
=2×17=34
(iii) From the above property, we have:
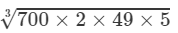
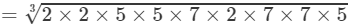 (∵∵ 700=2×2×5×5×7 and 49=7×7)
(∵∵ 700=2×2×5×5×7 and 49=7×7)
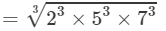
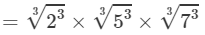
=2×5×7=70
(iv) From the above property, we have:
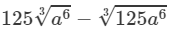
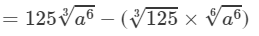 =125×a2−(5×a2)
=125×a2−(5×a2)
(∵  =a×a=a2 and
=a×a=a2 and 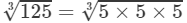 =5)
=5)
=125a2−5a2=120a2
Question 5: Find the cube root of each of the following rational numbers:
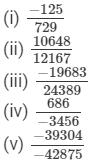
Answer 5: (i) Let us consider the following rational number:
- 125/729
Now
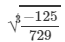
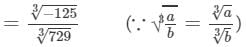
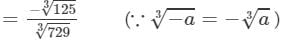
= - 5/9 (∵∵ 729=9×9×9 and 125 = 5×5×5729=9×9×9 and 125 = 5×5×5)
(ii) Let us consider the following rational number:
10648/12167
Now
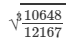

Cube root by factors:
On factorising 10648 into prime factors, we get:
10648=2×2×2×11×11×1110648=2×2×2×11×11×11
On grouping the factors in triples of equal factors, we get:
10648={2×2×2}×{11×11×11}10648=2×2×2×11×11×11
Now, taking one factor from each triple, we get:
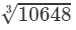 =2×11=22106483=2×11=22
=2×11=22106483=2×11=22
Also
On factorising 12167 into prime factors, we get:
12167=23×23×2312167=23×23×23
On grouping the factors in triples of equal factors, we get:
12167={23×23×23}12167=23×23×23
Now, taking one factor from the triple, we get:
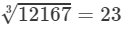
Now
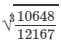
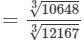
= 22/23
(iii) Let us consider the following rational number:
-19683/24389
Now,
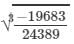
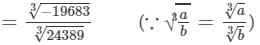
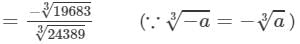
Cube root by factors:
On factorising 19683 into prime factors, we get:
19683=3×3×3×3×3×3×3×3×319683=3×3×3×3×3×3×3×3×3
On grouping the factors in triples of equal factors, we get:
19683={3×3×3}×{3×3×3}×{3×3×3}19683=3×3×3×3×3×3×3×3×3
Now, taking one factor from each triple, we get:
 =3×3×3=27196833=3×3×3=27
=3×3×3=27196833=3×3×3=27
Also
On factorising 24389 into prime factors, we get:
24389=29×29×2924389=29×29×29
On grouping the factors in triples of equal factors, we get:
24389={29×29×29}24389=29×29×29
Now, taking one factor from each triple, we get:
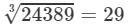
Now
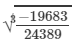
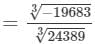
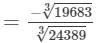
= -27/ 29
(iv) Let us consider the following rational number:
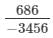
Now

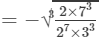 (686 and 3456 are not perfect cubes; therefore, we simplify it as 686/34566863456 by prime factorisation.)
(686 and 3456 are not perfect cubes; therefore, we simplify it as 686/34566863456 by prime factorisation.)
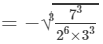
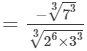
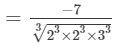
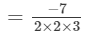
= -7/ 12
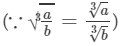
(v) Let us consider the following rational number:
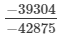
Now

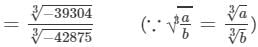
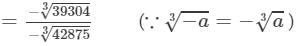
Cube root by factors:
On factorising 39304 into prime factors, we get:
39304=2×2×2×17×17×1739304=2×2×2×17×17×17
On grouping the factors in triples of equal factors, we get:
39304={2×2×2}×{17×17×17}39304=2×2×2×17×17×17
Now, taking one factor from each triple, we get:
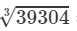 =2×17=34
=2×17=34
Also
On factorising 42875 into prime factors, we get:
42875=5×5×5×7×7×742875=5×5×5×7×7×7
On grouping the factors in triples of equal factors, we get:
42875={5×5×5}×{7×7×7}42875=5×5×5×7×7×7
Now, taking one factor from each triple, we get:
 =5×7=35
=5×7=35
Now

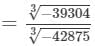
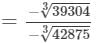
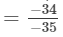
= 34/35
Question 6: Find the cube root of each of the following rational numbers:
(i) 0.001728
(ii) 0.003375
(iii) 0.001
(iv) 1.331
Answer 6: (i) We have:
0.001728=1728/1000000
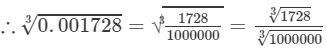
Now
On factorising 1728 into prime factors, we get:
1728=2×2×2×2×2×2×3×3×31728=2×2×2×2×2×2×3×3×3
On grouping the factors in triples of equal factors, we get:
1728={2×2×2}×{2×2×2}×{3×3×3}
Now, taking one factor from each triple, we get:
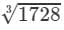 =2×2×3=1217283=2×2×3=12
=2×2×3=1217283=2×2×3=12
Also
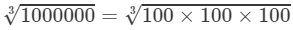 = 100
= 100
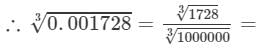 12/100 = 0.12
12/100 = 0.12
(ii) We have:
0.003375= 3375/ 10000000.003375=33751000000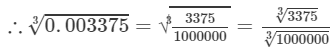
Now
On factorising 3375 into prime factors, we get:
3375=3×3×3×5×5×53375=3×3×3×5×5×5
On grouping the factors in triples of equal factors, we get:
3375={3×3×3}×{5×5×5}3375=3×3×3×5×5×5
Now, taking one factor from each triple, we get:
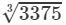 =3×5=1533753=3×5=15
=3×5=1533753=3×5=15
Also
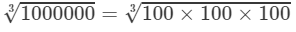 =10010000003=100×100×1003=100
=10010000003=100×100×1003=100
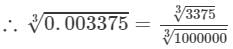 = 15/100 = 0.15
= 15/100 = 0.15
(iii) We have:
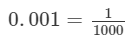
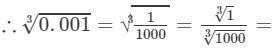 1/10 = 0.1
1/10 = 0.1
(iv) We have:
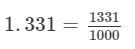
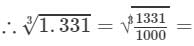
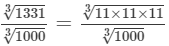 = 11/10 = 1.1
= 11/10 = 1.1
Question 7: Evaluate each of the following
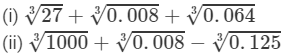
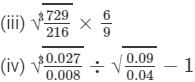
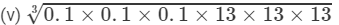
Answer 7:
(i) To evaluate the value of the given expression, we need to proceed as follows:
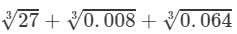
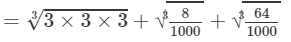
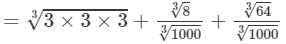
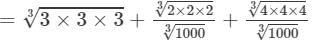
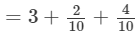
=3+0.2+0.4=3.6 Thus, the answer is 3.6.
(ii) To evaluate the value of the given expression, we need to proceed as follows:
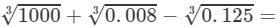
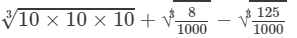
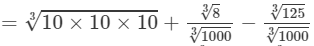
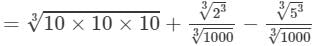
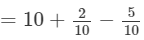
=10+0.2−0.5=9.7
Thus, the answer is 9.7.
(iii) To evaluate the value of the given expression, we need to proceed as follows:
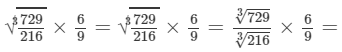
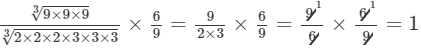
Thus, the answer is 1.
(iv) To evaluate the value of the expression, we need to proceed as follows:
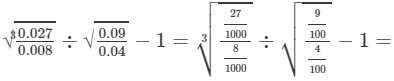
−1=1−1=0
Thus, the answer is 0.
(v) To evaluate the value of the expression, we need to proceed as follows:
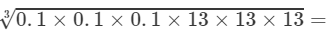
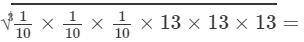
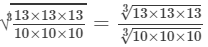 =13/10 =1.3
=13/10 =1.3
Thus, the answer is 1.3.
Question 8: Show that:
Answer 8:
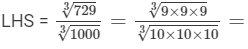 9/10
9/10
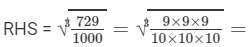
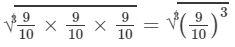 = 9/10
= 9/10
Because LHS is equal to RHS, the equation is true.
(ii)
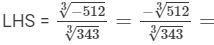
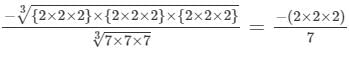 = -8/7
= -8/7
RHS =
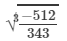
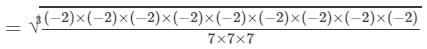
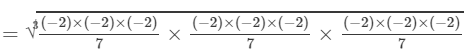
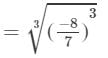
= -8/7
Because LHS is equal to RHS, the equation is true.
Question 9: Fill in the blanks:
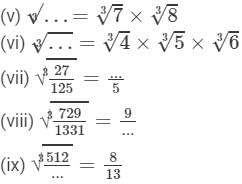
Answer 9:
(i) 5
 3×5
3×5
∵ 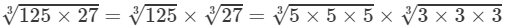
=5×3
=3×5=3×5 (Commutative law)
(ii) 8×8=648×8=64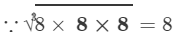
(iii) 3
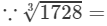 12=4×3
12=4×3
(iv) 20
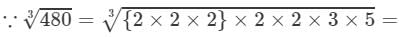
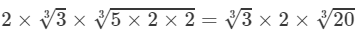
(v) 7×8=567×8=56
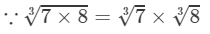
(vi) 4×5×6=1204×5×6=120
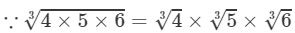
(vii) 3
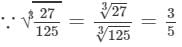
(viii) 11
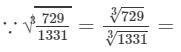 9/11
9/11
(ix) 13×13×13=2197
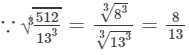 13×13×13=2197
13×13×13=2197
Question 10: The volume of a cubical box is 474.552 cubic metres. Find the length of each side of the box.
Answer 10: Volume of a cube is given by:
V=s3V=s3, where s = side of the cube
Now
s3=474.552 cubic metres
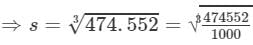
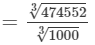 To find the cube root of 474552, we need to proceed as follows:
To find the cube root of 474552, we need to proceed as follows:
On factorising 474552 into prime factors, we get:
474552=2×2×2×3×3×3×13×13×13474552=2×2×2×3×3×3×13×13×13
On grouping the factors in triples of equal factors, we get:
474552={2×2×2}×{3×3×3}×{13×13×13}474552=2×2×2×3×3×3×13×13×13
Now, taking one factor from each triple, we get:
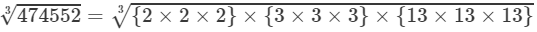 =2×3×13=78
=2×3×13=78
Also
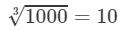
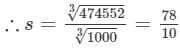 = 7.8
= 7.8
Thus, the length of the side is 7.8 m.
Question 11: Three numbers are to one another 2 : 3 : 4. The sum of their cubes is 0.334125. Find the numbers.
Answer 11: Let the numbers be 2x, 3x and 4x.
According to the question:
(2x)3+(3x)3+(4x)3=0.334125⇒8x3+27x3+64x3=0.334125⇒8x3+27x3+64x3=0.334125⇒99x3=0.334125 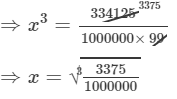
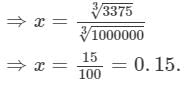
Thus, the numbers are:
2×0.15=0.30 3×0.15=0.454×0.15=0.60 Question 12: Find the side of a cube whose volume is 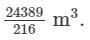
Answer 12: Volume of a cube with side s is given by:
V=s3V=s3
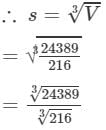
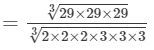 (By prime factorisation)
(By prime factorisation)
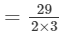
= 29/6
Question 13: Evaluate:
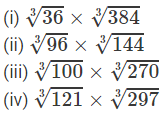
Answer 13:
(i) 36 and 384 are not perfect cubes; therefore, we use the following property:
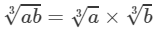 for any two integers a and b
for any two integers a and b
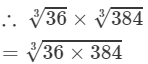
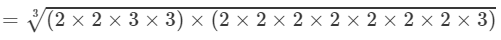 (By prime factorisation)
(By prime factorisation)
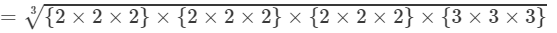
=2×2×2×3=24
Thus, the answer is 24.
(ii) 96 and 122 are not perfect cubes; therefore, we use the following property:
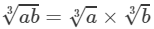 for any two integers a and b
for any two integers a and b
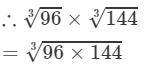
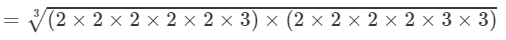 (By prime factorisation)
(By prime factorisation)
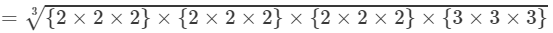
=2×2×2×3=24 Thus, the answer is 24.
(iii) 100 and 270 are not perfect cubes; therefore, we use the following property:
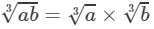 for any two integers a and b
for any two integers a and b
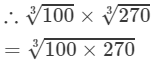
 (By prime factorisation)
(By prime factorisation)
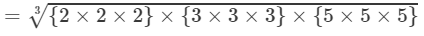
=2×3×5=30 Thus, the answer is 30.
(iv) 121 and 297 are not perfect cubes; therefore, we use the following property: 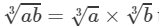 for any two integers a and b
for any two integers a and b
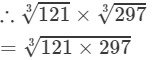
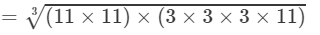 (By prime factorisation)
(By prime factorisation)
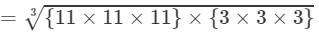
=11×3=33 Thus, the answer is 33.
Question 14: Find The cube roots of the numbers 3048625, 20346417, 210644875, 57066625 using the fact that
(i) 3048625 = 3375 × 729
(ii) 20346417 = 9261 × 2197
(iii) 210644875 = 42875 × 4913
(iv) 57066625 = 166375 × 343
Answer 14:
(i) To find the cube root, we use the following property:
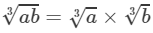 for two integers a and b
for two integers a and b
Now
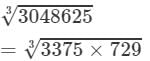
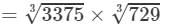 (By the above property)
(By the above property)
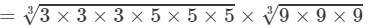 (By prime factorisation)
(By prime factorisation)
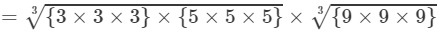
=3×5×9=135 Thus, the answer is 135.
(ii) To find the cube root, we use the following property:
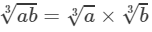 for two integers a and b
for two integers a and b
Now
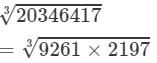
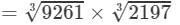 (By the above property)
(By the above property)
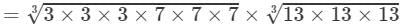 (By prime factorisation)
(By prime factorisation)
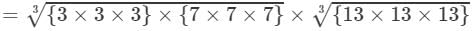
=3×7×13=273 Thus, the answer is 273.
(iii) To find the cube root, we use the following property:
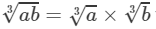 for two integers a and b
for two integers a and b
Now

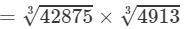 (By the above property)
(By the above property)
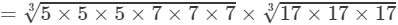 (By prime factorisation)
(By prime factorisation)
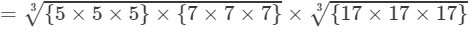
=5×7×17=595 Thus, the answer is 595.
(iv) To find the cube root, we use the following property:
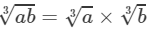 for two integers a and b
for two integers a and b
Now

 (By the above property)
(By the above property)
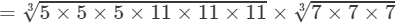 (By prime factorisation)
(By prime factorisation)
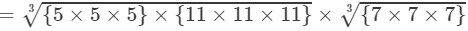
=5×11×7=385 Thus, the answer is 385.
Question 15: Find the units digit of the cube root of the following numbers:
(i) 226981
(ii) 13824
(iii) 571787
(iv) 175616
Answer 15: (i) Cube root using units digit:
Let us consider the number 226981.
The unit digit is 1; therefore, the unit digit of the cube root of 226981 is 1.
(ii) Cube root using units digit:
Let us consider the number 13824.
The unit digit is 4; therefore, the unit digit of the cube root of 13824 is 4.
(iii) Cube root using units digit:
Let us consider the number 571787.
The unit digit is 7; therefore, the unit digit of the cube root of 571787 is 3.
(iv) Cube root using units digit:
Let us consider the number 175616.
The unit digit is 6; therefore, the unit digit of the cube root of 175616 is 6.
Question 16: Find the tens digit of the cube root of each of the numbers in Q. No. 15.
Answer 16: (i) Let us consider the number 226981.
The unit digit is 1; therefore, the unit digit of the cube root of 226981 is 1.
After striking out the units, tens and hundreds digits of the given number, we are left with 226.
Now, 6 is the largest number, whose cube is less than or equal to 226 (63<226<7363<226<73).
Therefore, the tens digit of the cube root of 226981 is 6.
(ii) Let us consider the number 13824.
The unit digit is 4; therefore, the unit digit of the cube root of 13824 is 4.
After striking out the units, tens and hundreds digits of the given number, we are left with 13.
Now, 2 is the largest number, whose cube is less than or equal to 13 (23<13<3323<13<33).
Therefore, the tens digit of the cube root of 13824 is 2.
(iii) Let us consider the number 571787.
The unit digit is 7; therefore, the unit digit of the cube root of 571787 is 3.
After striking out the units, tens and hundreds digits of the given number, we are left with 571.
Now, 8 is the largest number, whose cube is less than or equal to 571 (83<571<9383<571<93).
Therefore, the tens digit of the cube root of 571787 is 8.
(iv) Let us consider the number 175616.
The unit digit is 6; therefore, the unit digit of the cube root of 175616 is 6.
After striking out the units, tens and hundreds digits of the given number, we are left with 175.
Now, 5 is the largest number, whose cube is less than or equal to 175 (53<175<6353<175<63).
Therefore, the tens digit of the cube root of 175616 is 5.
FAQs on RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-4) - RD Sharma Solutions for Class 8 Mathematics
| 1. How do you find the cube root of a number? |  |
| 2. Can a negative number have a cube root? |  |
| 3. How do you determine if a number is a perfect cube? |  |
| 4. What is the cube of a negative number? |  |
| 5. How do you solve problems involving cubes and cube roots? |  |