Ex-10.6, Congruent Triangles, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q. (1) In Δ ABC, if ∠ A = 40° and ∠ B = 60°. Determine the longest and shortest sides of the triangle.
Solution:
Given that in Δ ABC, ∠ A = 40° and ∠ B = 60°
We have to find longest and shortest side
We know that,
Sum of angles in a triangle 180°
∠ A + ∠ B + ∠ C = 180°
40° + 60° + ∠ C = 180°
∠ C = 180° – ((10)0°) = 80°
∠ C = 80°
Now,
=> 40° < 60° < 80° = ∠ A < ∠ B < ∠ C
=> ∠ C is greater angle and ∠ A is smaller angle.
Now, ∠ A < ∠ B < ∠ C
=> BC < AAC < AB [Side opposite to greater angle is larger and side opposite to smaller angle is smaller]
AB is longest and BC is smallest or shortest side.
Q. (2) In a Δ ABC, if ∠ B = ∠ C = 45°, which is the longest side?
Solution: Given that in Δ ABC,
∠ B = ∠ C = 45°
We have to find longest side
We know that.
Sum of angles in a triangle =180°
∠ A + ∠ B + ∠ C = 180°
∠ A + 45° + 45° = 180°
∠ A = 180° – (45° + 45°) = 180° – 90° = 90°
∠ A = 90°
Q. (3) In Δ ABC, side AB is produced to D so that BD = BC. If ∠ B = 60° and ∠ A = 70°. prove that: (i) AD > CD (ii) AD > AC
Sol: Given that, in Δ ABC, side AB is produced to D so that BD = BC.
∠ B = 60°, and ∠ A = 70°
To prove,
(i) AD > CD (ii) AD > AC
First join C and D
We know that,
Sum of angles in a triangle =180°
∠ A + ∠ B + ∠ C = 180°
70° + 60° + ∠ C = 180°
∠ C = 180° – (130°) = 50°
∠ C = 50°
∠ ACB = 50°……(i)
And also in Δ BDC
∠ DBC =180 – ∠ ABC [ABD is a straight angle]
180 – 60° = 120°
and also BD = BC[given]
∠ BCD = ∠ BDC [Angles opposite to equal sides are equal]
Now,
∠ DBC + ∠ BCD + ∠ BDC = 180° [Sum of angles in a triangle =180°]
=> 120° + ∠ BCD + ∠ BCD = 180°
=> 120° + 2∠ BCD = 180°
=> 2∠ BCD = 180° – 120° = 60°
=> ∠ BCD = 30°
=> ∠ BCD = ∠ BDC = 30° ….(ii)
Now, consider Δ ADC.
∠ BAC => ∠ DAC = 70° [given]
∠ BDC => ∠ ADC = 30° [From (ii)]
∠ ACD = ∠ ACB+ ∠ BCD
= 50° + 30°[From (i) and (ii)] =80°
Now, ∠ ADC < ∠ DAC < ∠ ACD
AC < DC < AD [Side opposite to greater angle is longer and smaller angle is smaller]
AD > CD and AD > AC
Hence proved
Or,
We have,
∠ ACD > ∠ DAC and ∠ ACD > ∠ ADC
AD > DC and AD> AC [Side opposite to greater angle is longer and smaller angle is smaller]
Q. (4) Is it possible to draw a triangle with sides of length 2 cm, 3 cm and 7 cm?
Sol:
Given lengths of sides are 2cm, 3cm and 7cm.
To check whether it is possible to draw a triangle with the given lengths of sides
We know that,
A triangle can be drawn only when the sum of any two sides is greater than the third side.
So, let’s check the rule.
2 + 3 ≯ 7 or 2 + 3 < 7
2 + 7 > 3
and 3 + 7 > 2
Here 2 + 3 ≯ 7
So, the triangle does not exit.
Q. (5) O is any point in the interior of Δ ABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC > (1/2)(AB + BC +CA)
Solution:
Given that O is any point in the interior of Δ ABC
To prove
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC > (1/2)(AB + BC +CA)
We know that in a triangle the sum of any two sides is greater than the third side.
So, we have
In Δ ABC
AB + BC > AC
BC + AC > AB
AC + AB > BC
In Δ OBC
OB + OC > BC…….(i)
In Δ OAC
OA + OC > AC……(ii)
In Δ OAB
OA + OB > AB……(iii)
Now, extend (or) produce BO to meet AC in D.
Now, in Δ ABD, we have
AB + AD > BD
AB + AD > BO + OD …….(iv) [BD = BO + OD]
Similarly in Δ ODC, we have
OD + DC > OC……(v)
(i) Adding (iv) and (v), we get
AB + AD + OD + DC > BO + OD + OC
AB + (AD + DC) > OB + OC
AB + AC > OB + OC ……(vi)
Similarly, we have
BC + BA > OA + OC……(vii)
and CA+ CB > OA + OB……(viii)
(ii) Adding equation (vi), (vii) and (viii), we get
AB + AC + BC + BA + CA + CB > OB + OC + OA + OC + OA + OB => 2AB + 2BC + 2CA > 2OA + 2OB + 2OC
=> 2(AB + BC + CA) > 2(OA + OB + OC)
=> AB + BC + CA > OA + OB + OC
(iii) Adding equations (i), (ii) and (iii)
OB + OC + OA + OC + OA + OB > BC + AC + AB
2OA + 2OB + 2OC > AB + BC + CA
We get = 2(OA + OB + OC) > AB + BC +CA
(OA + OB + OC) > (1/2)(AB + BC +CA)
Q. (6) Prove that the perimeter of a triangle is greater than the sum of its altitudes.
Solution:
Given, Δ ABC in which AD ⊥ BC, BE ⊥ AC and CF ⊥ AB.
To prove,
AD + BE + CF < AB + BC + AC
Figure:
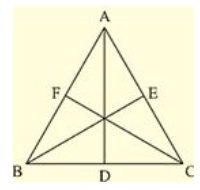
Proof:
We know that of all the segments that can be drawn to a given line, from a point not lying on it, the perpendicular distance i.e, the perpendicular line segment is the shortest.
Therefore
AD ⊥ BC
AB > AD and AC > AD
AB + AC > 2AD ……(i)
BE ⊥ AC
BA > BE and BC > BE
BA + BC > 2BE ……(ii)
CF ⊥ AB
CA > CF and CB > CF
CA + CB > 2CF ……(iii)
Adding (i), (ii) and (iii), we get
AB + AC + BA + BC + CA + CB > 2AD + 2BE + 2CF
2AB + 2BC + 2CA > 2(AD + BE + CF)
AB + BC + CA > AD + BE + CF
The perimeter of the triangle is greater than that the sum of its altitudes
Hence proved
Q. (7) In Fig., prove that:
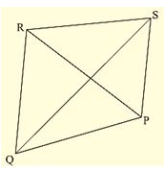
(i) CD + DA + AB + BC > 2AC
(ii) CD + DA + AB > BC
Solution:
To prove
(i) CD + DA + AB + BC > 2AC
(ii) CD + DA+ AB > BC
From the given figure,
We know that, in a triangle sum of any two sides is greater than the third side
(i) So,
In Δ ABC, we have
AB + BC > AC ……(i)
In Δ ADC, we have
CD + DA > AC……(ii)
Adding (i) and (ii), we get
AB + BC + CD + DA > AC + AC
AB + BC + CD + DA > 2AC
(ii) Now, In Δ ABC, we have,
AB +AC > BC……(iii)
And in Δ ADC, we have
CD + DA > AC
Add AB on both sides
CD + DA + AB > AC + AB
From equation (iii) and (iv), we get,
CD + DA + AB > AC + AB > BC
CD + DA + AB > BC
Hence proved
Q. (8) Which of the following statements are true (T) and which are false (F)?
(i) Sum of the three sides of a triangle is less than the sum of its three altitudes.
(ii) Sum of any two sides of a triangle is greater than twice the median drown to the third side
(iii) Sum of any two sides of a triangle is greater than the third side.
(iv) Difference of any two sides of a triangle is equal to the third side.
(v) If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it
(vi) Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
Solution:
(i) False (F)
Reason: Sum of these sides of a triangle is greater than sum of its three altitudes
(ii) True (T)
(iii) True (T)
(iv) False (F)
Reason: The difference of any two sides of a triangle is less than third side
(v) True (T)
Reason: The side opposite to greater angle is longer and smaller angle is shorter in a triangle
(vi) True (T).
Reason: The perpendicular distance is the shortest distance from a point to a line not containing it.
Q. (9) Fill in the blanks to make the following statements true.
(i) In a right triangle the hypotenuse is the ___ side.
(ii) The sum of three altitudes of a triangle is ___ than its perimeter.
(iii) The sum of any two sides of a triangle is ___ than the third side.
(iv) If two angles of a triangle are unequal, then the smaller angle has the ___ side opposite to it.
(v) Difference of any two sides of a triangle is ___ than the third side.
(vi) If two sides of a triangle are unequal, then the larger side has ___ angle opposite to it.
Solution:
(i) In a right triangle the hypotenuse is the largest side
Reason: Since a triangle can have only one right angle, other two angles must be less than 90
The right angle is the largest angle.
Hypotenuse is the largest side.
(ii) The sum of three altitudes of a triangle is less than its perimeter.
(iii) The sum of any two sides of a triangle is greater than the third side. (iv) If two angles of a triangle are unequal, then the smaller angle has the smaller side opposite to it.
(v) Difference of any two sides of a triangle is less than the third side.
(vi) If two sides of a triangle are unequal, then the larger side has greater angle opposite to it.
FAQs on Ex-10.6, Congruent Triangles, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What are congruent triangles? |  |
| 2. How can we prove two triangles congruent? |  |
| 3. What is the importance of congruent triangles in mathematics? |  |
| 4. How do congruent triangles help in solving problems involving triangles? |  |
| 5. What are some real-life examples where congruent triangles are used? |  |





















