Class 9 Math: Sample Question Paper- 6 (With Solutions) PDF Download
SECTION - A
Questions 1 to 20 carry 1 mark each
Q.1. Which one of the following is not equal to 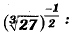
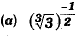
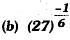
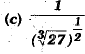
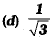
Ans: (a)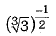
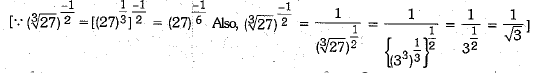
Q.2. A is the foot of perpendicular from a point (4, -9,7) on x-axis. The coordinates of A are
(a) (4,0,0)
(b) (0,-9,0)
(c) (0,0,7)
(d) (-4,9,-7)
Ans: Choice (a) is correct.
We know that on x-axis, y = 0 and z = 0. Therefore, the coordinates of foot of perpendicular A are (4,0,0).
Q.3. Ordinate of all points on the X-axis is
(a) 0
(b) 1
(c) -1
(d) any number
Ans: (a) Ordinate of all points on the X-axis is zero. Because ordinate (or y-coordinate) of a point is its perpendicular distance from the X-axis measured along the X-axis. If ordinate of all points on the X-axis, then this perpendicular distance will be zero, so ordinate will be zero.
Q.4. If (2,0) is a solution of the linear equation 2x + 3y = k, then the value of k is
(a) 4
(b) 6
(c) 5
(d) 2
OR
If the point (3, a) lies on the line represented by the linear equation, 2x - 3y = 5, then the value of a is:
(a) 1/3
(b) 1/2
(c) 1/4
(d) 1
Ans: Correct option : (a)
Explanation: Put x = 2, y = 0 in the equation 2x + 3y = k
2(2) + 3(0) = k
4 + 0 = k
Hence, k = 4
Or
Correct option: (a)
2(3) - 3 (a) = 5
(Putting x = 3 and y = a in the given equation)
⇒ 6-3a = 5
⇒ 6 - 5 = 3a
⇒ a=1/3
Q.5. In the given figure, AB || CD and EF || AC, if ∠BAC = 75°, then ∠DEF is :
(a) 75°
(b) 90°
(c) 105°
(d) 120°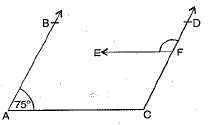
Ans: (c) 105°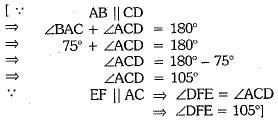
Q.6. The sixth term from the beginning of the G.P. 8, 4, 2, . . . is :
(a) 1/2
(b) 1/4
(c) 1/16
(d) -1/4
Ans: Choice (b) is correct.
The given sequence is a G.P. with a = 8, r =1/2
The nth term an from the beginning is given by an arn-1
The sixth term a6 from beginning is given by a6 - 8x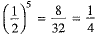
Q.7. √2 is a polynomial of degree
(a) 0
(b) 1
(c) 2
(d) 3
Ans: 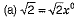
So. √2 is a polynomial of degree 0.
Q.8. The angles of a quadrilateral are in the ratio 3:4:5:6. The respective angles of the quadrilateral are
(a) 60°, 80°, 100°, 120°
(c) 120°, 60°, 80°, 100°
(b) 120°, 100°, 80°, 60°
(d) 80°, 100°, 120°, 60°
Ans: Correct option: (a)
Explanation: Let the angles be 3x, 4x, 5x and 6x,
Then
3x + 4x + 5x + 6x - 360°
⇒ 18x = 360°
⇒ x = 20°
The angles are 60°, 80°, 100° and 120°
Q.9. The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Then the ratio of surface areas of the original balloon to the resulting new balloon is:
(a) 4:1
(b) 2:1
(c) 1:4
(d) 1:2
Ans: (c) 1 : 4
[∵ Surface area of a spherical balloon whose radius is 7 cm
= 4π x 7 x 7 cm2
Surface area of a spherical balloon whose radius is 14 cm
= 4π x 14 x 14 cm2
∴ Ratio of surface areas = 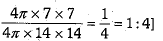
Q.10. In a distribution, N = 100, sum of absolute values of deviations from mean = 84, then the mean deviation from mean is
(a) 8.4
(b) 0.84
(c) 80.4
(d) 0.084
Ans: Choice (b) is correct.
Given, sum of absolute values of deviations from mean = 84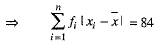
Questions 11 to 15 carry one mark each
Q.11. When a non-negative number is added to both sides of a linear equation, then its solution is .............
Ans: When a non-negative number is added to both sides of a linear equation, then its solution is unaffected.
Q.12. Two supplementary angles are in ratio 2 : 7. Find the measures of angles.
OR
In fig. if AB || CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.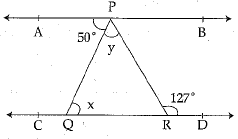
Ans: 2x + 7x= 180° ⇒ x = 20°
So the angles are
2x = 2 x 20° = 40°
and 7x - 7 x 20° '= 140°
So two angles are 40° and 140°
Or
x = ∠APQ - 50° (Alternate interior angles)
50° + y = 127° (Alternate interior angles)
⇒ y = 127°-50°
= 77°
Q.13. If all angles o f a quadrilateral are equal, it is a ................
Ans: rectangle
Q.14. The value of cot 5° cot 10° cot 15° ... cot 85° is equal to ___________ .
Ans: 1
cot 5° cot 10° cot 15° ... cot 85°
= (cot 5° cot 85°)(cot 10° cot 80°)(cot 15° cot 75°)...(cot 40° cot 50°)cot 45°
= {cot 5° cot (90° - 5°) } {cot 10 cot(90° - 10°)}{cot 15° cot (90° - 15) ..{cot 40° cot(90° - 40°) } cot 45°
= (cot 5° tan 5°)(cot 10° tan 10°)(cot 15° tan 15°)...(cot 40° tan 40°) cot 45°
= (1) (1) (1). . .(1) (1) = 1
Or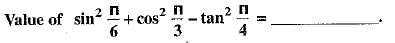
Ans: -1/2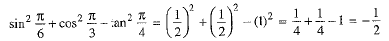
Q.15. A frequency polygon is constructed by plotting frequency of the class interval and the ...........
Ans: A frequency polygon is constructed by plotting frequency of the class interval and the mid volume of class.
Questions 16 to 20 carry one mark each
Q.16. π is an irrational number
Or
In 56x = 1252, then x = 1
Ans: True :
OR
True :
56x = (53)2 ⇒ 56x = 56 ⇒ x = 1
Q.17. In the given figure, the ratio QR:RS is 2:1 . If the area of ΔPQS is 60 cm2, find the area of ΔPRS.
Or
Find the area of a triangle whose sides are 7 cm, 24 cm and 25 cm.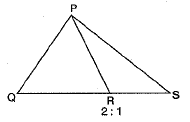
Ans: Since QS is divided by R in the ratio
QR : RS = 2 : 1
thus,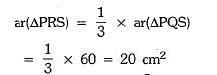
Or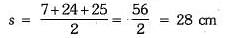
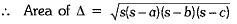
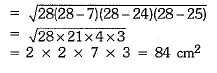
Q.18. Let f = {(1,1), (2, 3), (0, -1), (-1, -3)} be a linear function from Z into Z. Find f(x).
Ans: Let f(x) = ax + b be a linear function.
Also, (0, -1), (1, 1) ∈ R, ∴ f(o) = 0 + b = b, f(1) = a + b
Thus, - 1 =f(0) = b and 1 = f(1) = a + b ⇒ a = 1 - b = 1 -(-1) = 2
Hence, f(x) = 2 x - 1.
Q.19. The angles of quadrilateral are in the ratio 3:5:9:13 . Find all the angles of the quadrilateral.
Ans: Given, the ratio of the angles of quadrilateral are 3:5:9:13.
Let the angles of the quadrilateral are 3x, 5x, 9x and 13x,
We know that, sum of angles of a quadrilateral = 360°
∴ 3x + 5x + 9x +13x = 360°
⇒ 30x = 360° ⇒ x = 12°
∴ Angles of the quadrilateral are
3x = 3 x 12 = 36°,
5x = 5 x 12 = 60°,
9x = 9 x 12 =108°
and 13x = 13 x 12 =156°
Q.20. Area of a triangle is b x h
Ans: False
Area of triangle is 1/2 x b x h
SECTION - B
Question number 21 to 26, carry 2 marks each.
Q.21. Find the value of
Ans: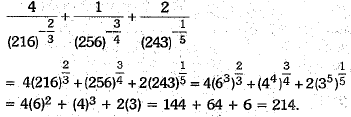
Q.22. Solve the following equation :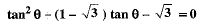
Ans: The given equation is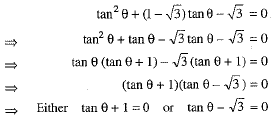
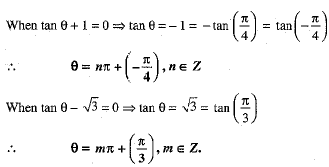
Q.23. A die is thrown 300 times and the outcomes are noted as given below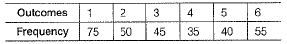
If a die is thrown at random, then find the probability of getting prime number
(i) 1
(ii) 2
(iii) 3
(iv) 5
Ans: Here, total number of trials = 300
(i) We know that, 1 is not a prime number, so we cannot determine the probability of prime number.
(ii) P (getting 2 on a die)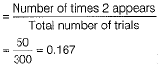
(iii) P (getting 3 on a die)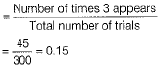
(iv) P (getting 5 on a die)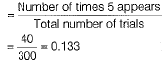
Q.24. In given fig., AD = BC and ∠BAD = ∠ABC, then prove that ∠ACB = ∠BDA.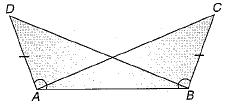
Ans: In ΔBAD and ΔABC
AD = BC [Given]
∠BAD = ∠ABC [Given]
AB = AB [Common]
ΔBAD ≌ ΔABC [By SAS congruence rule]
∴ ∠BDA = ∠ACB [By cpct]
Q.25. The sides of a triangular field are 51 m, 37 m and 20 m. Find the number of rose beds that can be prepared in the field if each rose bed occupies a space of 6 sq. m.
Or
The base (non-equal side) of an isosceles triangle is 8 cm. Find its area, if the perimeter of the triangle is 32 cm.
Ans: Let ABC be the given triangular field in which AB = 51 m, BC = 37 m and AC = 20 m.
In ΔABC, we have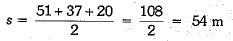
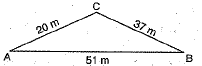

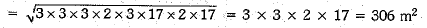
Since each rose bed occupies a spate of 6 sq. m.
Required number of rose beds in the field = 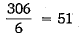
Or
Here, perimeter of an isosceles triangle = 32 cm
Base or non-equal side of the triangle = 8 cm
Let each equal side of the isosceles triangle be x cm.
∴ x + x + 8 = 32
⇒ 2x = 32 - 8 = 24
⇒ x = 12 cm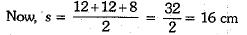
Area of the triangle by using Heron’s formula
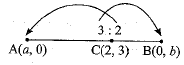
Q.26. A line cuts x-axis at point A and y-axis at point B. The point (2,3) divides AB in the ratio of 3: 2. Find the equation of the line.
Ans: Let the equation of the line AB which cuts the x-axis at point A and y-axis at point B be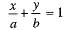 ...(1)
...(1)
It is given that the line (1) cuts the x-axis, then by putting y = 0 in (1), we have x = a
∴ The coordinates of the point A are A(a, 0).
Similarly, the line (1) cuts the y-axis then by putting x = 0 in (1), we have
y=b
∴ The coordinates of the point B are 5(0, b).
Let C be a point C(2, 3) which divides AB in the ratio 3 : 2.
If C(2, 3) divides AB in the ratio 3 : 2, i.e., AC: CB = 3 : 2, then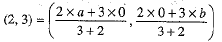
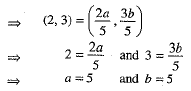
∴ The required equation of the line AB is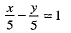
⇒ x + y = 5
Or
Given that P(3, 2, -4), Q (5, 4, -6) and R (9, 8, -10) are collinear. Find the ratio in which Q divides RS
Ans: Let Q divides PR in the ratio k : 1. Then, the co-ordinates of Q are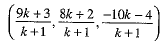
According to the question, we have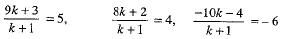
On solving these equations, we get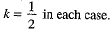
Thus, Q divides PR in the ratio 1/2 : 1 or 1: 2.
SECTION - C
Question 27 to 34, carry 3 marks each
Q.27. Factorise: 8x3 + 20x2 + 6x - 9
Or
If (x + 1) and (x + 2) are the factors of x3 + 3x2 - 3ax + β, then find α and β.
Ans: Let p(x) = 8x3 + 20x2 + 6x - 9
By hit and trial method, we find that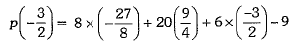
= -27 + 45 - 9 - 9 = 0
∴ (2x + 3) is a factor of p(x).
Now, by long division method, we obtain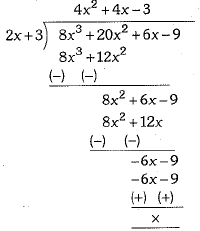
∴ p(x) = (2x + 3) (4x2 + 4x -3)
= (2x + 3) (4x2 4- 6x - 2x - 3)
= (2x + 3) {2x (2x + 3) - 1(2x + 3)}
= (2x + 3) (2x + 3) (2x - 1)
Or
Let p(x) = x3 + 3x2 - 3αx + β
Since (x + 1) and (x + 2) are factors of p(x)
∴ Put x = -1 and -2, we obtain
p(-1) = (-1)3 + 3(-1)2 - 3α(-1) + β = 0
⇒ -1 + 3 + 3α + β = 0
⇒ 3α + β = -2 ...(i)
p(-2) = (-2)3 + 3(-2)2 - 3α(-2) + β = 0
⇒ -8 + 12 + 6a + β = 0
⇒ 6α + β = - 4 ...(ii)
Subtracting (i) from (ii). we have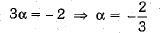
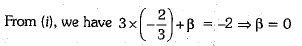
Hence, values of α and β are α = -1/2 and β =0.
Q.28. Using principle of mathematical induction, prove that
x3n - y3n is divisible by (x - y) for all n ∈ N.
Ans: Let P(n) : x3n - y3n is divisible by (x - y) for all n ∈ N ...(1)
When n = 1, P(1) - x3x1 - y3x1] = x3 - y3 = (x - y)(x2 + xy + y2) which is divisible by (x - y).
∴ P(1) is true.
Let us assume that P(k) is true for any natural number k.
i.e., P(k) : x3k - y3k is divisible by (x - y).
i.e., x3k - y3k = m(x - y), where m is some integer. ...(2)
Now, we have to prove that P(k + 1) is also true.
i.e., P(k + 1) : x3(k + 1) - y3(k + 1) is divisible by (x - y).
Now, x3(k + 1) -y3(k + 1) = 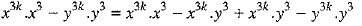
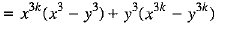
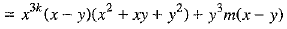 [using (2)]
[using (2)]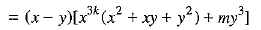
which is divisible by (x - y).
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, P(n) : x3n - y3n is divisible by (x - y) for all n ∈ N.
Q.29. In the given figure, D and E are the points on the base BC of ΔABC such that BD = CE, AD = AE and ∠ADE = ∠AED.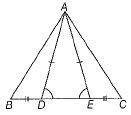
Prove that ΔABE ≌ ΔACD.
Ans: Given In ΔABC, D and E are the points on the base BC and BD = CE, AD = AE and ∠ADE = ∠AED.
To prove ΔABE ≌ ΔACD
Proof In ΔABE and ΔACE , we have
AD = AE [given]
BD = CE [given]
and ∠ADB = ∠AEC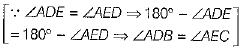
∴ ΔABD = ΔACE [by SAS congruence rule]
Hence, AB = AC [by CPCT]
Now, in ΔABE and ΔACD, we have
ΔACD, we have
AB = AC [proved above]
BE = CD
[∵ BD = CE ⇒ BD + DE = CE + ED ⇒ BE = CD]
and ∠ABE = ∠ACD
[∵ angles opposite to equal sides are equal]
∴ ΔABE ≌ ΔACD [by SAS congruence rule]
Hence proved
Q.30. ABCD is a square. If ∠PQR = 90° and PB - QC = DR, prove that ∠QPR = 45°.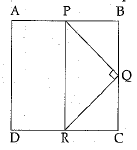
Ans: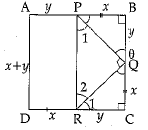
Let PB = QC = DR =x
If BQ = y , then RC = y (∴ BC = DC)
By Pythagoras theorem,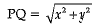 ...(i)
...(i)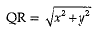 ...(ii)
...(ii)
From (i) and (ii) PQ = QR
∴ ∠QPR = ∠PRQ = 45°
Q.31. A circular park of radius 10 m is situated in a colony. Three students Ashok, Raman and Kanaihya are standing at equal distances on its circumference each having a toy telephone in his hands to talk each other about Honesty, Peace and Discipline. Find the length of the string of each phone.
Ans: Let us assume, A, B and C be the position of three students Ashok, Raman and Kanaihya respectively on the circumference of the circular park with centre O and radius 10 m. Since the centre of circle coincides with the centroid of the equilateral ΔABC.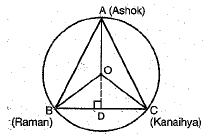
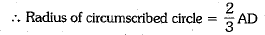
⇒ 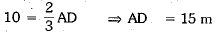
Now, AD ⊥ BC and let AB = BC = CA = x
⇒ 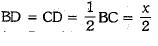
In rt ∠ed ∠BDA, ∠D = 90°
AB2 = BD2 + AD2 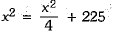
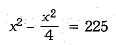
⇒ 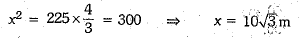
Thus, the length of each string is 10√3 m.
Q.32. The Mean and Standard Deviation of a group of 100 observations were found to be 20 and 3, respectively. Later on, it was found that three observations were incorrect, which were recorded as 21, 21 and 18. Find the Mean and Standard Deviation if the incorrect observations are omitted.
Ans: We have n = 100, 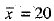 and
and 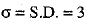
We know that: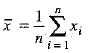
⇒ 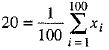
⇒ 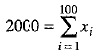 ...(1)
...(1)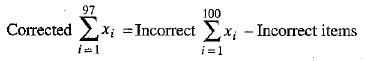
= 2000-(21 +21 + 18) [using (1)]
= 2000 - 60
= 1940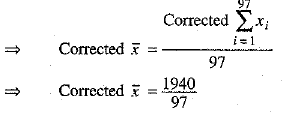
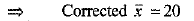 ...(2)
...(2)
Now, 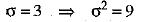
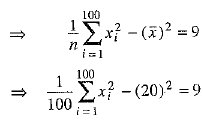
⇒ 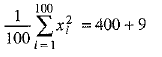
⇒ 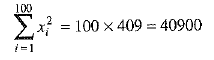 ...(3)
...(3)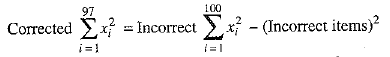
= 40900 - [(21 )2 + (21)2 + (18)2] [using (3)]
= 40900 - [441 + 441 + 324]
= 40900 - (1206)
= 3969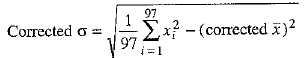
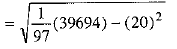 [using (2)]
[using (2)]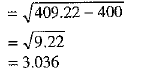
Hence, the new Mean and Standard Deviation are 20 and 3.036.
Q.33. How many solution(s) of the equation 2(x + y) + 3 =2y are there on the
(i) number line
(ii) cartesian plane?
Also, show it by the graph.
Ans: Given, equation is 2 (x + y) + 3 = 2y
⇒ 2x + 2y + 3 = 2y ⇒ 2x = - 3 ⇒ x = -3/2
which is a linear equation in one variable. (i) On number line, the solution of the given equation is unique (one solution).
i.e. 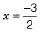
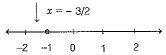
(ii) In cartesian plane,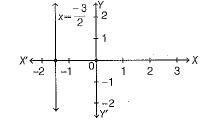
The number of solutions are infinite as solutions are in the form 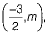 where m can be any real number.
where m can be any real number.
Q.34. Cards marked with numbers 2 to 101 are placed in a box and mixed thoroughly. One card is drawn from this box. Find the probability that the number on the card is:
(a) a number less than 14
(b) a number which is a perfect square
(c) a prime number less than 29
OR
Three coins are tossed simultaneously 400 times and following frequencies of the outcomes were recorded
(i) Find the probability of getting no head
(ii) Find the probability of getting one head
(iii) Find the probability of getting exactly two heads
Ans: Here, we have
Total number of cards marked with number 2 to 101 = 100
(a) Cards marked with number < 14 are with number 2 to 13 .
⇒ Total number of cards having a number < 14 = 12
∴ P (that a number 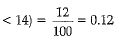
(b) Cards with number as a perfect square from 2 to 101 are :
4,9,16,25,36,49, 64,81,100
⇒ Total number of cards having a perfect square number = 9
⇒ P(that a perfect square number)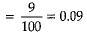
(c) Cards with a prime number < 29 are :
2, 3, 5,7, 11, 13, 17, 19, 23 .
⇒ Total number of cards having a prime number < 29 = 9
⇒ P (that a prime number < 20)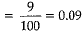
OR
Given : Total numbers of outcomes = 400
Now, outcomes for getting no head
= 400 - (103 + 124 + 98)
= 75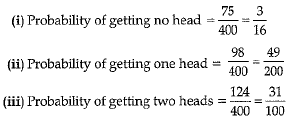
SECTION - D
Question 35 to 40 carry 4 marks each
Q.35. Simplify: 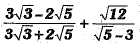
Or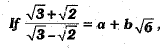 find the values of a and b.
find the values of a and b.
Ans: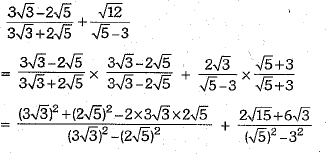
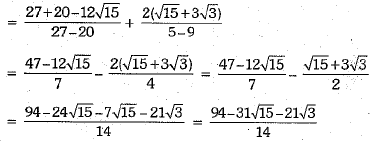
Or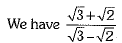
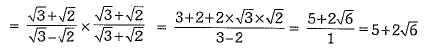
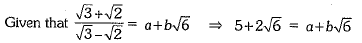
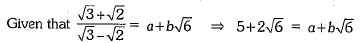
On comparing the rational and irrational parts, we have a = 5 and b = 2
Q.36. Prove that:
cos A cos 2A cos 4A cos 8A= 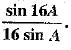
OR
Prove that: cos3 A + cos3 (120° + A) + cos3 (240° + A) = 3/4 cos 3A.
Ans. We have
L.H.S. = cos A cos 2A cos 4A cos 8A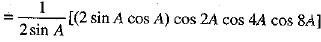 [Multiplying and dividing by 2 sin A]
[Multiplying and dividing by 2 sin A]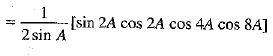 [∵ 2 sinθ cosθ = sin 2θ]
[∵ 2 sinθ cosθ = sin 2θ]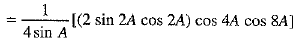 [Multiplying and dividing by 2]
[Multiplying and dividing by 2]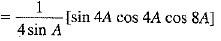
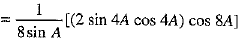 [Multiplying and dividing by 2]
[Multiplying and dividing by 2]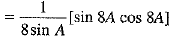
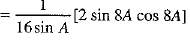 [Multiplying and dividing by 2]
[Multiplying and dividing by 2]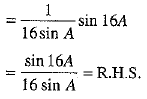
OR
We know that
cos 3A = 4 cos3 A - 3 cos A
⇒ 4 cos3 A = 3 cos A + cos 3A
⇒ 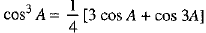 ...(1)
...(1)
L.H.S. = cos3 A + cos3 (120° + A) + cos3 (240° + A)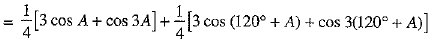
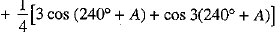 [using (1)]
[using (1)]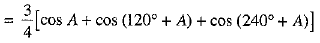
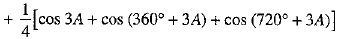
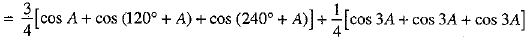
[∵ cos (720° + 3A) = cos 3A; cos (360° + 3A) = cos 3A]
= 3/4 [cos A + cos (240° + A) + cos (120° + A)] + 3/4 cos 3A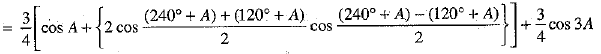
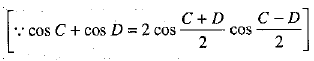
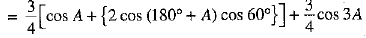
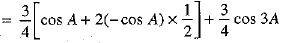 [∵ cos (180° + A) = - cos A]
[∵ cos (180° + A) = - cos A]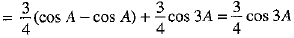
= R.H.S.
Q.37. Calculate the mean and mode for the following data.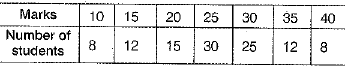
Or
Calculate the mean, median and mode for the following data.
23, 25, 28, 25, 16, 23, 17, 22, 25, 25
Ans. The table for marks and number of students is given below
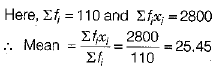
We know that mode is the value, which contain highest frequency.
Here, we see in the given table that 30 is the highest frequency and its corresponding marks is 25.
Hence, mode of the given data is 25.
OR
Firstly, write the given data in ascending order.
16, 17, 22, 23, 23, 25, 25, 25, 25, 28
We can represent above data in the following table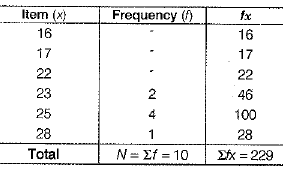
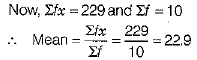
Here, n = 10 [even]
∴ 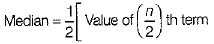
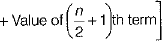
= 1/2 [Value of 5th term + Value of 6th term]
= 1/2(23 + 25) =24
Mode = Value of variable which occurs most frequently = 25
Q.38. Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11 cm.
Ans. ∠Y = 30° and ∠Z = 30°
Sum of three sides XY + YZ + ZX = 11 cm
Required: To construct ΔXYZ
Steps of construction:
1. Draw a line segment say PQ = 11 cm
(∵ XY + YZ + ZX = 11 cm)
2. Draw ∠KPQ = 60° (∵ ∠Y = 30°)
And ∠LQP = 90° (∵ ∠Z = 90°)
3. Bisect the ∠KPQ and ∠LQP . Let these intersect at point X.
4. Let MN intersect PQ at Y and RS intersect l PQ at Z
5. Join XY and XZ.
Then XYZ is the required triangle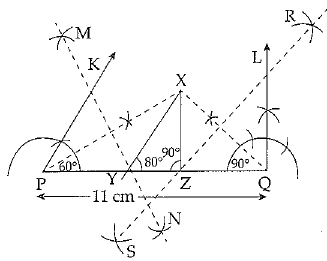
Q.39. Shanti Sweets Stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25 cm x 20 cm x 5 cm and the smaller of dimensions 15 cm x 12 cm x 5 cm. For all the overlaps, 5 % of the total surface area is required extra. If the cost of the cardboard , is INR 4 for 1000 cm2, find the cost of cardboard required for supplying 250 boxes of each kind.
Ans. Total surface area of smaller box
= 2(lb + bh + hl)
= 2 (15 x 12 + 12 x 5 + 5 x 15)
= 2 (180 + 60 + 75) = 630 cm2
Extra area of cardboard required for overlapping = 5/100 x 630 = 31.50 cm2
∴ Total area of cardboard required for each smaller box = 630 + 31.50 — 661.50 cm2
Total surface area of bigger box
= 2 ( lb + bh + hl)
= 2 (25 x 20 + 20 x 5 + 5 x 25)
= 2 (500 + 100 + 125) = 2(725) = 1450 cm2
Extra area of cardboard required for overlapping = 5/100 x 1450 = 72.50 cm2
∴ Total area of cardboard required for each bigger box
= 1450 cm2 + 72.50 cm2 = 1522.50 cm2
Total area of cardboard required for 250 such boxes each smaller and bigger
= 250 x (661.50 + 1522.50) = 250 x 2184 = 546000 cm2
Now, total cost of cardboard at the rate of INR 4 for 1000 cm2 = 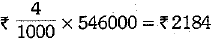
Q.40. How many words can be formed out of the letters of the word ‘MATHEMATICS ’. In how many words of the letters of the word so that the consonants occur together.
Ans. Given word is ‘MATHEMATICS’ and there are 11 letters in the given word, out of which two M ’s, two A’s and two T’s are alike and remaining 5 letters are distinct.
∴ Number of possible arrangements of all letters taken all at a time = 11!/2!2!2!
∴ Number of words formed of the letters of the word = 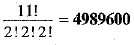
There are 7 consonants in the given word (i.e., M, M, T, T, H, C, S).
When the consonants occur together, let us treat them as one letter (MMTTHCS).
Now there are 5 letters (i.e., MMTTHCS, A, A, E, I), out of which two A’s are alike and rest are distinct.
∴ Number of possible arrangements of these 5 letters taken all at a time = 5!/2!
Corresponding to each such arrangement, the 7 consonants can be arranged amongst themselves in 7!/2!2! ways. [∵ M and T occur two times]
∴ Number of arrangements in which consonants are together = 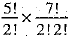
∴ Number of words in which consonants occur together = 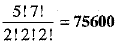
FAQs on Class 9 Math: Sample Question Paper- 6 (With Solutions)
| 1. What is the format of the Class 9 Math Sample Question Paper- 6? |  |
| 2. How many questions are included in the Class 9 Math Sample Question Paper- 6? |  |
| 3. Are the solutions provided for all the questions in the Class 9 Math Sample Question Paper- 6? |  |
| 4. How can the Class 9 Math Sample Question Paper- 6 help in exam preparation? |  |
| 5. Can the Class 9 Math Sample Question Paper- 6 be used for self-study? |  |



















