NCERT Solutions for Class 8 Maths - Algebraic Expressions and Identities - 2 (Exercise 8.3 and 8.4)

Exercise 8.3
Q1. Carry out the multiplication of the expressions in each of the following pairs.
(i) 4p, q + r
Ans: (4p) × (q + r) = (4p × q) + (4p × r) = 4pq + 4pr
(ii) ab, a – b
Ans: (ab) × (a - b) = (ab × a) + [ab×(-b)] = a2b - ab2
(iii) a + b, 7a2b2
Ans: (a + b) × (7a2 b2) = (a × 7a2b2) + (b × 7a2b2) = 7a3b2 + 7a2b3
(iv) a2 – 9, 4a
Ans: (a2 - 9) × (4a) = (a2 × 4a) + ( - 9) × (4a) = 4a3 - 36a
(v) pq + qr + rp, 0
Ans: (pq + qr + rp) × 0 = (pq × 0) + (qr × 0) + (rp × 0) = 0
Q2. Complete the table.
Ans: The table can be completed as follows. 
Q3. Find the product.
(i) (a2) × (2a22) × (4a26)
(ii) 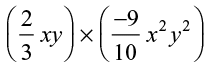
(iii) 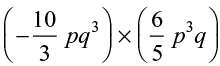
(iv) x × x2 × x3 × x4
Ans: 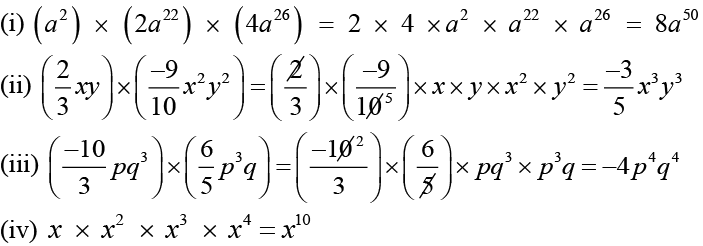
Q4. (a) Simplify 3x(4x – 5) + 3 and find its values for
(i) x = 3 and
(ii) x = 1/2
(b) Simplify a(a2 + a + 1) + 5 and find its value for
(i) a = 0,
(ii) a = 1
(iii) a = –1.
Ans:
(a) 3x (4x − 5) + 3 = 12x2 − 15x + 3
(i) For x = 3,
=12x2 - 15x + 3
=12(3)2 - 15(3) + 3
= 108 - 45 + 3
= 66
(ii) For x = 1/2
=12x2 - 15x + 3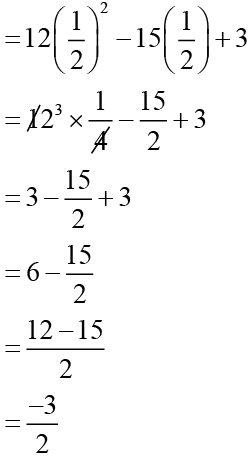
(b) a(a2 + a + 1) + 5 = a3 + a2 + a + 5
(i) For a = 0, a3 + a2 + a + 5 = 0 + 0 + 0 + 5 = 5
(ii) For a = 1, a3 + a2 + a + 5 =(1)3 +(1)2 + 1 + 5
= 1 + 1 + 1 + 5 = 8
(iii) For a = - 1, a3 + a2 + a + 5 =(-1)3 +(-1)2 + (-1) + 5
=- 1 + 1 - 1 + 5 = 4
Q5: Solve the following
(a) Add: p (p - q), q (q - r) and r (r - p)
Ans: First expression = p (p - q) = p2 - pq
Second expression = q (q - r) = q2 - qr
Third expression = r (r - p) = r2 - pr
Adding the three expressions, we obtain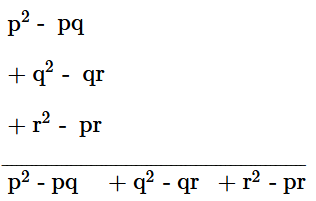
Therefore, the sum is p2 - pq + q2 - qr + r2 - pr
(b) Add: 2x(z – x – y) and 2y(z – y – x)
Ans: First expression = 2x (z - x - y) = 2xz - 2x2 - 2xy
Second expression = 2y (z - y - x) = 2yz - 2y2 - 2yx
Adding the two expressions, we obtain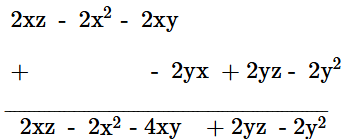
Therefore, the sum is 2xz - 2x2 - 4xy + 2yz - 2y2
(c) Subtract: 3l(l – 4m + 5n) from 41(10n + 3m + 2l)
Ans: 3l (l - 4m + 5n) = 3l2 - 12lm + 15ln
= 4l (10n - 3m + 2l) = 40ln - 12lm + 8l2
Subtracting these expressions, we obtain
8l2 - 12lm + 40ln
3l2 - 12lm + 15ln
(-) (+) (-)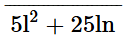
Therefore, the result is 5l2 + 25ln
(d) Subtract: 3a(a + b + c) – 2b(a – b + c) from 4c(–a + b + c)
Ans: 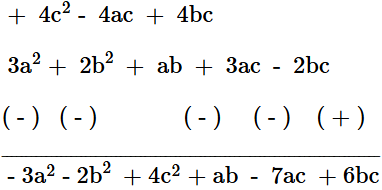
Therefore, the result is - 3a2 - 2b2 + 4c2 + ab - 7ac + 6bc
Exercise 8.4
Q1. Multiply the binomials.
(i) (2x + 5) and (4x – 3)
(ii) (y – 8) and (3y – 4)
(iii) (2.5l – 0.5m) and (2.5l + 0.5m)
(iv) (a + 3b) and (x + 5)
(v) (2pq + 3q2 ) and (3pq – 2q2)
(vi) 
Ans:
(i) (2x + 5) and (4x – 3)
= 2x × 4x – 2x × 3 + 5 × 4x – 5 × 3
= 8x2 – 6x + 20x -15
= 8x2 + 14x -15
(ii) ( y – 8)and (3y – 4)
= y × 3y – 4y – 8 × 3y + 32
= 3y2 – 4y – 24y + 32
= 3y2 – 28y + 32
(iii) (2.5l – 0.5m) and (2.5l + 0.5m)
= 2.5l × 2.5 l + 2.5l × 0.5m – 0.5m × 2.5l – 0.5m × 0.5m
= 6.25l2 + 1.25 lm – 1.25 lm – 0.25 m2
= 6.25l2– 0.25 m2
(iv) (a + 3b) and (x + 5)
= ax + 5a + 3bx + 15b
(v) (2pq + 3q2) and (3pq – 2q2)
= 2pq × 3pq – 2pq × 2q2 + 3q2 × 3pq – 3q2 × 2q2
= 6p2q2 – 4pq3 + 9pq3 – 6q4
= 6p2q2 + 5pq3 – 6q4
(vi) 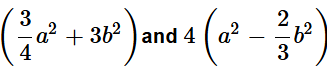
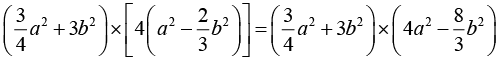
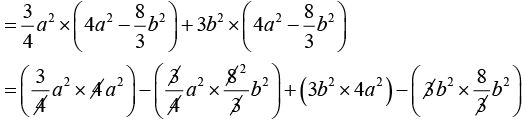
= 3a4 – 2a2 b2 + 12 a2 b2 – 8b4
= 3a4 + 10a2 b2 – 8b4
Q2. Find the product.
(i) (5 – 2x) (3 + x)
= 5 (3 + x) – 2x (3 + x)
=15 + 5x – 6x – 2x2
= 15 – x -2 x 2
(ii) (x + 7y) (7x – y)
= x(7x-y) + 7y ( 7x-y)
=7x2 – xy + 49xy – 7y2
= 7x2 – 7y2 + 48xy
(iii) (a2+ b) (a + b2)
= a2 (a + b2) + b(a + b2)
= a3 + a2b2 + ab + b3
= a3 + b3 + a2b2 + ab
(iv) (p2– q2) (2p + q)
= p2 (2p + q) – q2 (2p + q)
=2p3 + p2q – 2pq2 – q3
= 2p3 – q3 + p2q – 2pq2
Q3. Simplify.
(i) (x2– 5) (x + 5) + 25
= x3 + 5x2 – 5x – 25 + 25
= x3 + 5x2 – 5x
(ii) (a2+ 5) (b3+ 3) + 5
= a2b3 + 3a2 + 5b3 + 15 + 5
= a2b3 + 5b3 + 3a2 + 20
(iii) (t + s2)(t2 – s)
= t (t2 – s) + s2(t2 – s)
= t3 – st + s2t2 – s3
= t3 – s3 – st + s2t2
(iv) (a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)
= (a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)
=(ac – ad + bc – bd) + (ac + ad – bc – bd) + (2ac + 2bd)
= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd
= 4ac
(v) (x + y)(2x + y) + (x + 2y)(x – y)
= 2x2 + xy + 2xy + y2 + x2 – xy + 2xy – 2y2
= 3x2 + 4xy – y2
(vi) (x + y)(x2– xy + y2)
= x3 – x2y + xy2 + x2y – xy2 + y3
= x3 + y3
(vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x + 12y
= 2.25x2 + 6xy + 4.5x – 6xy – 16y2 – 12y – 4.5x + 12y
= 2.25x2 – 16y2
(viii) (a + b + c)(a + b – c)
= a2 + ab – ac + ab + b2 – bc + ac + bc – c2
= a2 + b2 – c2 + 2ab
|
81 videos|423 docs|31 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Algebraic Expressions and Identities - 2 (Exercise 8.3 and 8.4)
| 1. What are algebraic expressions and how are they formed? |  |
| 2. What are the types of algebraic expressions? |  |
| 3. What are the key algebraic identities? |  |
| 4. How can we simplify algebraic expressions using identities? |  |
| 5. How do you factor algebraic expressions using identities? |  |

















