Class 9 Maths Question Answers - Areas of Parallelograms
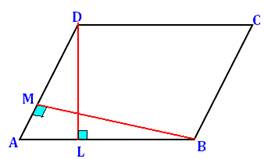
Q1. In a parallelogram ABCD, it is being given that AB = 12 cm and the altitude corresponding to the sides AB and AD are DL = 5 cm and BM = 8 cm respectively. Find AD.
∵ Area of a parallelogram = base x height
∴ Area of parallelogram ABCD = AB x DL = 12 cm x 5 cm = 60 cm2 Again, area of parallelogram ABCD = AD x BM
∴ AD x BM = 60 cm2 [∵ ar (parallelogram ABCD) = 60 cm2]
⇒ AD x 8 cm = 60 cm2 [∵ BM = 8 cm (Given)]
⇒ AD = (60/8) cm
= (15/2) cm = 7.5 cm
Thus, the required length of AD is 7.5 cm.
Q2. Find the area of a trapezium whose parallel sides are 9 cm and 5 cm respectively and the distance between these sides is 8 cm.
Let ABCD be a trapezium such that AD || BC. Let us join BD.
∵ Area of a triangle = (1/2)x base x height
∴ Area of ΔABD = (1/2)x AD x height
= (1/2)x 5 cm x 8 cm = 20 cm2
ar (ΔBCD) = (1/2)x base x height
= (1/2)x BC x height
= (1/2)x 9 cm x 8 cm
= 36 cm2
Now, ar (trapezium ABCD) = ar (D ABD) + ar (D BCD)
= 20 cm2 + 36 cm2
= 56 cm2
Q3. In the adjoining figure, find the area of the trapezium ABCD.
∵ DEC is a right triangle.
∴ ar (ΔDEC) = (1/2)x base x height
= (1/2)x 8 x 15 cm2
= 60 cm2 ar (rectangle ABED) = length x breadth
= 10 cm x 15 cm = 150 cm2
Now, ar (trapezium ABCD) = ar (rectangle ABED) + ar (ΔDEC)
= 150 cm2 + 60 cm2 = 210 cm2
Thus, the required area of trapezium ABCD = 210 cm2.
Q 4. In the figure BD || CA, E is mid-point of CA and BD = (1/2) CA.
Prove that ar (ΔABC) = 2 ar (ΔDBC)
Join D and E
∵ BD = CE and BD || CE
∴ BCED is a parallelogram. ⇒ ΔDBC and ΔEBC are on the same base BC and between the same parallels,
∴ ar (ΔDBC) = ar (ΔEBC) ... (1)
In ΔABC, BE is a median,
∴ ar (ΔFBC) = (1/2)ar (ΔABC)
Now, ar (ΔABC) = ar (ΔEBC) + ar (ΔABE)
Also, ar (ΔABC) = 2 ar (ΔEBC)
∴ ar (ΔABC) = 2 ar (ΔDBC)
Q5. In the adjoining figure, ABCD is a quadrilateral in which diagonal BD = 12 cm. If AL ⊥ BD and CM ⊥ BD such that AL = 6 cm and CM = 4 cm, find the area of quadrilateral ABCD.
The diagonal BD divides the given quadrilateral into two triangles BDC and ABD.
Since, area of a triangle = (1/2)x base x altitude
∴ Area of ΔABD = (1/2)x BD x AL
= (1/2)x 12 cm x 6 cm
= 36 cm2
Area of ΔBCD = (1/2)x base x altitude
=(1/2)x BD x CM
= (1/2)x 12 cm x 4 cm
= 24 cm2.
Now, ar (quadrilateral ABCD) = ar (ΔABD) + ar (ΔBCD)
⇒ ar (quadrilateral ABCD) = 36 cm2 + 24 cm2
= 60 cm2
Thus, the required area of quadrilateral ABCD
= 60 cm2.
Q6. Find the area of the following quadrilateral.
∵ APB is a right triangle.
∴ AB2 – BP2 = AP2
⇒ 102 – 82 = AP2
⇒ 100 – 64 = AP2
⇒ AP = 36 = 6 cm
Since, ar (rt ΔAPB) =(1/2)x base x altitude
∴ ar (ΔAPB) =(1/2)x 6 cm x 8 cm
= 24 cm2
Similarly, ar (rt ΔCQD) = 24 cm2 Area of rectangle BCQP
= length x breath = 6 cm x 8 cm = 48 cm2
Now, area of quadrilateral ABCD
= ar (rt ΔAPB) + ar (rectangle BCQP) + ar (rt ΔCQD)
= 24 cm2 + 48 cm2 + 24 cm2
= 96 cm2
Thus, the required area of the quadrilateral ABCD
= 96 cm2.
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths Question Answers - Areas of Parallelograms
| 1. What is the formula to calculate the area of a parallelogram? |  |
| 2. How do I find the height of a parallelogram if only the base and area are given? |  |
| 3. Can the base and height of a parallelogram be any two sides of the parallelogram? |  |
| 4. How is the area of a triangle related to the area of a parallelogram? |  |
| 5. What is the difference between a parallelogram and a triangle in terms of their areas? |  |