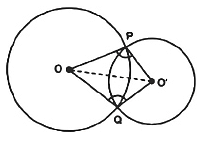
Q.1. Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Solution: Consider the following diagram
 In ΔPOO’ and ΔQOO’ OP = OQ (Radius of circle 1)
In ΔPOO’ and ΔQOO’ OP = OQ (Radius of circle 1)
O’P = O’Q (Radius of circle 2)
OO’ = OO’ (Common arm)
So, by SSS congruency, ΔPOO’ ≅ ΔQOO’
Thus, ∠OPO’ = ∠OQO’ (proved).
Q.2. Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6, find the radius of the circle.
Solution:

Here, OM ⊥ AB and ON ⊥ CD. is drawn and OB and OD are joined.
We know that AB bisects BM as the perpendicular from the centre bisects chord.
Since AB = 5 so,
BM = AB / 2
Similarly, ND = CD / 2 = 11 / 2
Now, let ON be x.
So, OM = 6 − x.
Consider ΔMOB,
OB2 = OM2 + MB2
Or,
OB2 = 36 + x2 - 12x + 25 / 4 .....(1)
Consider ΔNOD,
OD2 = ON2 + ND2
Or
OD2 = x2 + 121 / 4 ....(2)
We know, OB = OD (radii)
From equation 1 and equation 2 we get
36 + x2 - 12x + 25 / 4 = x2 + 121 / 4
12x = 36 + 25 / 4 - 121 / 4

12x = 48 / 4 = 12
x = 1
Now, from equation (2) we have,
OD2 = 12 + (121 / 4)
Or OD = (5 / 2) × √5 cm
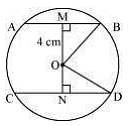
Q.3. The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at a distance 4 cm from the centre, what is the distance of the other chord from the centre?
Solution: Consider the following diagram
 Here AB and CD are 2 parallel chords. Now, join OB and OD.
Here AB and CD are 2 parallel chords. Now, join OB and OD.
Distance of smaller chord AB from the centre of the circle = 4 cm
So, OM = 4 cm
MB = AB / 2 = 3 cm
Consider ΔOMB
OB2 = OM2 + MB2
Or, OB = 5cm
Now, consider ΔOND,
OB = OD = 5 (since they are the radii)
ND = CD / 2 = 4 cm
Now, OD2 = ON2 + ND2
Or, ON = 3 cm.
Q.4. Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Solution: Consider the diagram
 Here AD = CE
Here AD = CE
We know, any exterior angle of a triangle is equal to the sum of interior opposite angles.
So,
∠DAE = ∠ABC + ∠AEC (in ΔBAE) ...............(i)
DE subtends ∠DOE at the centre and ∠DAE in the remaining part of the circle.
So,
∠DAE = (½)∠DOE ...........(ii)
Similarly, ∠AEC = (½)∠AOC ...........(iii)
Now, from equation (i), (ii), and (iii) we get,
(½)∠DOE = ∠ABC + (½)∠AOC
Or, ∠ABC = (½) [∠DOE - ∠AOC] (hence proved).
Q.5. Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
Solution:
 To prove: A circle drawn with Q as centre, will pass through A, B and O (i.e. QA = QB = QO)
To prove: A circle drawn with Q as centre, will pass through A, B and O (i.e. QA = QB = QO)
Since all sides of a rhombus are equal,
AB = DC
Now, multiply
(½) on both sides (½)AB = (½)DC
So, AQ = DP
BQ = DP
Since Q is the midpoint of AB,
AQ = BQ
Similarly,
RA = SB
Again, as PQ is drawn parallel to AD,
RA = QO
Now, as AQ = BQ and RA = QO we get,
QA = QB = QO (hence proved).
Q.6. ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE, = AD.
Solution:
 Here, ABCE is a cyclic quadrilateral. In a cyclic quadrilateral, the sum of the opposite angles is 180°.
Here, ABCE is a cyclic quadrilateral. In a cyclic quadrilateral, the sum of the opposite angles is 180°.
So, ∠AEC + ∠CBA = 180°
As ∠AEC and ∠AED are linear pair,
∠AEC + ∠AED = 180°
Or, ∠AED = ∠CBA … (1)
We know in a parallelogram; opposite angles are equal.
So, ∠ADE = ∠CBA … (2)
Now, from equations (1) and (2) we get,
∠AED = ∠ADE
Now, AD and AE are angles opposite to equal sides of a triangle,
∴ AD = AE (proved).
Q.7. AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.
Solution:
 Here chords AB and CD intersect each other at O.
Here chords AB and CD intersect each other at O.
Consider ΔAOB and ΔCOD,
∠AOB = ∠COD (They are vertically opposite angles)
OB = OD (Given in the question)
OA = OC (Given in the question)
So, by SAS congruency, ΔAOB ≅ ΔCOD
Also, AB = CD (By CPCT)
Similarly, ΔAOD ≅ ΔCOB
Or, AD = CB (By CPCT)
In quadrilateral ACBD, opposite sides are equal.
So, ACBD is a parallelogram.
We know that opposite angles of a parallelogram are equal.
So, ∠A = ∠C
Also, as ABCD is a cyclic quadrilateral,
∠A + ∠C = 180°
⇒ ∠A + ∠A = 180°
Or, ∠A = 90°
As ACBD is a parallelogram and one of its interior angles is 90°, so, it is a rectangle.
∠A is the angle subtended by chord BD. And as ∠A = 90°, therefore, BD should be the diameter of the circle. Similarly, AC is the diameter of the circle.
Q.8. Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90° – (½)A, 90° – (½)B and 90° – (½)C.
Solution: Consider the following diagram
 Here, ABC is inscribed in a circle with center O and the bisectors of ∠A, ∠B and ∠C intersect the circumcircle at D, E and F respectively.
Here, ABC is inscribed in a circle with center O and the bisectors of ∠A, ∠B and ∠C intersect the circumcircle at D, E and F respectively.
Now, join DE, EF and FD
As angles in the same segment are equal, so,
∠FDA = ∠FCA ..............(i)
∠FDA = ∠EBA .............(ii)
By adding equations (i) and (ii) we get,
∠FDA + ∠EDA = ∠FCA + ∠EBA
Or, ∠FDE = ∠FCA + ∠EBA = (½)∠C + (½)∠B
We know, ∠A + ∠B + ∠C = 180°
So, ∠FDE = (½)[∠C + ∠B] = (½)[180° - ∠A]
∠FDE = [90 - (∠A / 2)]
In a similar way,
∠FED = [90° - (∠B / 2)] °
And,
∠EFD = [90° - (∠C / 2)] °.
Q.9. Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Solution: The diagram will be
 Here, ∠APB = ∠AQB (as AB is the common chord in both the congruent circles.)
Here, ∠APB = ∠AQB (as AB is the common chord in both the congruent circles.)
Now, consider ΔBPQ, ∠APB = ∠AQB
So, the angles opposite to equal sides of a triangle.
∴ BQ = BP.
Q.10. In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Solution: Consider this diagram
 Here, join BE and CE.
Here, join BE and CE.
Now, since AE is the bisector of ∠BAC,
∠BAE = ∠CAE
Also,
∴ arc BE = arc EC
This implies, chord BE = chord EC
Now, consider triangles ΔBDE and ΔCDE,
DE = DE (It is the common side)
BD = CD (It is given in the question)
BE = CE (Already proved)
So, by SSS congruency, ΔBDE ΔCDE.
Thus, ∴∠BDE = ∠CDE
We know, ∠BDE = ∠CDE = 180°
Or, ∠BDE = ∠CDE = 90°
∴ DE ⊥ BC (hence proved).
 In ΔPOO’ and ΔQOO’ OP = OQ (Radius of circle 1)
In ΔPOO’ and ΔQOO’ OP = OQ (Radius of circle 1)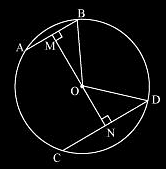
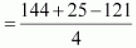
 Here AB and CD are 2 parallel chords. Now, join OB and OD.
Here AB and CD are 2 parallel chords. Now, join OB and OD.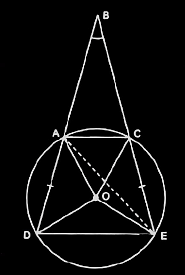 Here AD = CE
Here AD = CE To prove: A circle drawn with Q as centre, will pass through A, B and O (i.e. QA = QB = QO)
To prove: A circle drawn with Q as centre, will pass through A, B and O (i.e. QA = QB = QO)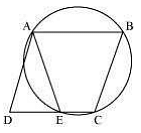 Here, ABCE is a cyclic quadrilateral. In a cyclic quadrilateral, the sum of the opposite angles is 180°.
Here, ABCE is a cyclic quadrilateral. In a cyclic quadrilateral, the sum of the opposite angles is 180°.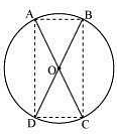 Here chords AB and CD intersect each other at O.
Here chords AB and CD intersect each other at O. Here, ABC is inscribed in a circle with center O and the bisectors of ∠A, ∠B and ∠C intersect the circumcircle at D, E and F respectively.
Here, ABC is inscribed in a circle with center O and the bisectors of ∠A, ∠B and ∠C intersect the circumcircle at D, E and F respectively.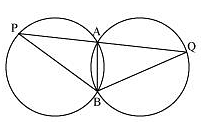 Here, ∠APB = ∠AQB (as AB is the common chord in both the congruent circles.)
Here, ∠APB = ∠AQB (as AB is the common chord in both the congruent circles.)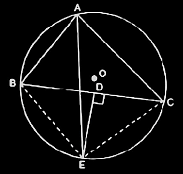 Here, join BE and CE.
Here, join BE and CE.























