Chapter 2 - Powers (Ex-2.3) - Class 8 Math RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1:
Express the following numbers in standard form:
(i) 6020000000000000
(ii) 0.00000000000943
(iii) 0.00000000085
(iv) 846 × 107
(v) 3759 × 10−4
(vi) 0.00072984
(vii) 0.000437 × 104
(viii) 4 ÷ 100000
Answer 1:
To express a number in the standard form, move the decimal point such that there is only one digit to the left of the decimal point.
(i) 6020000000000000 = 6.02 x 1015 (The decimal point is moved 15 places to the left.)
(ii) 0.0000000000943 = 9.43 x 10−12 (The decimal point is moved 12 places to the right.)
(iii) 0.00000000085 = 8.5 x 10−10 (The decimal point is moved 10 places to the right.)
(iv) 846 x 107 = 8.46 x 102 x 107 = 8.46 x 109 (The decimal point is moved two places to the left.)
(v) 3759 x 10−4 = 3.759 x 103 x 10−4 = 3.759 x 10−1 (The decimal point is moved three places to the left.)
(vi) 0.00072984 = 7.984 x 10−4 (The decimal point is moved four places to the right.)
(vii) 0.000437 x 104 = 4.37 x 10−4 x 104 = 4.37 x 100 = 4.37 (The decimal point is moved four places to the right.)
(viii) 4/100000 = 4 x 100000−1 = 4 x 10−5 (Just count the number of zeros in 1,00,000 to determine the exponent of 10.)
Question 2:
Write the following numbers in the usual form:
(i) 4.83 × 107
(ii) 3.02 × 10−6
(iii) 4.5 × 104
(iv) 3 × 10−8
(v) 1.0001 × 109
(vi) 5.8 × 102
(vii) 3.61492 × 106
(viii) 3.25 × 10−7
Answer 2:
(i) 4.83 x 107 = 4.83 x 1,00,00,000 = 4,83,00,000
(ii) 3.02 x 10−6 = 3.02/106 = 3.02/10,00,000 = 0.00000302
(iii) 4.5 x 104 = 4.5 x 10,000 = 45,000
(iv) 3 x 10−8 = 3/108 = 3/10,00,00,000 = 0.00000003
(v) 1.0001 x 109 = 1.0001 x 1,00,00,00,000 = 1,00,01,00,000
(vi) 5.8 x 102 = 5.8 x 100 = 580
(vii) 3.61492 x 106 = 3.61492 x 10,00,000 = 3614920
(viii) 3.25 x 10−7 = 3.25/107 = 3.25/1,00,00,000 = 0.000000325
Question 3: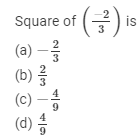
Answer 3:
(d) 4/9
To square a number is to raise it to the power of 2. Hence, the square of (−2/3) is 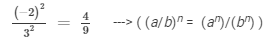
Question 4: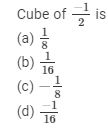
Answer 4:
(c) -1/8
The cube of a number is the number raised to the power of 3. Hence the cube of −1/2 is
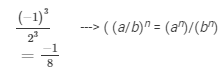
FAQs on Chapter 2 - Powers (Ex-2.3) - Class 8 Math RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What is the concept of powers in mathematics? |  |
| 2. How do you simplify expressions involving powers? |  |
| 3. What is the difference between a power and an exponent? |  |
| 4. How do you calculate negative powers? |  |
| 5. How are powers used in real-life applications? |  |
















