RD Sharma Solutions Ex-13.3, (Part -3), Linear Equation In Two Variables, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 15 : Draw the graph of y = | x |.
Ans. We are given,
y = |x|
Substituting x = 1 , we get y = 1
Substituting x = -1, we get y = 1
Substituting x = 2, we get y = 2
Substituting x = -2, we get y = 2
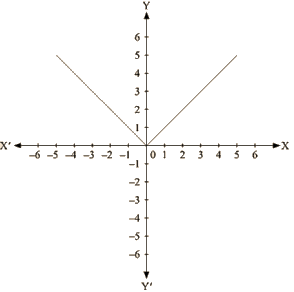
For every value of x, whether positive or negative, we get y as a positive number.
Q 16: Draw the graph of y = |x| + 2.
Ans. We are given,
Y = |x|+2
Substituting x = 0 we get y=2
Substituting x = I , we get y=3
Substituting x =-1 , we get Y = 3
Substituting x = 2, we get y = 4
Substituting x = -2, we get y = 4
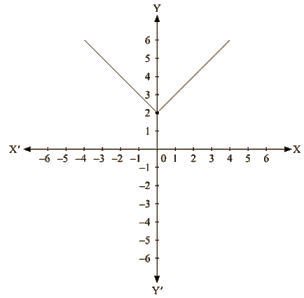
For every value of x, whether positive or negative, we get y as a positive number and the minimum value of y is equal to 2 units.
Q 17 : Draw the graphs of the following linear equations on the same graph paper: 2x + 3y = 12, x – y = 1 Find the coordinates of the vertices of the triangle formed by the two straight lines and the y-axis. Also, find the area of the triangle.
Ans. We are given,
2x +3y = 12
We get, 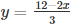
Now, substituting x = 0 in y 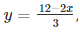 , we get
, we get
Substituting x = 6 in 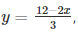 we get
we get
y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 6 |
| Y | 4 | 0 |
Plotting A(0,4) and E(6,0) on the graph and by joining the points , we obtain the graph of equation
2x+3y = 12.
We are given,
x – y = 1
We get, y = x – 1
Now, substituting x = 0 in y = x-1,
we get y = -1
Substituting x in y = x-1,
we get y = -2
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | -1 |
| Y | -1 | -2 |
Plotting D(0,) and E(-1,0) on the graph and by joining the points , we obtain the graph of equation x— y = I .
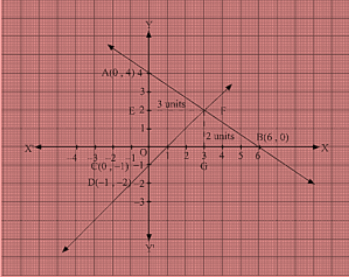
By the intersection of lines formed by 2x + 3y = 12 and x—y=1 on the graph, triangle ABC is formed on y axis.
Therefore, AC at y axis is the base of triangle ABC having AC = 5 units on y axis.
Draw FE perpendicular from F on y axis. FE parallel to x axis is the height of triangle ABC having FE = 3 units on x axis.
Therefore, Area of triangle ABC, say A is given by A = (Base x Height)/2 =(AC x FE)/2 = (5×3)/2 ⇒15/2 = 7.5 sq. units
Q 18 : Draw the graphs of the linear equations 4x – 3y + 4 = 0 and 4x + 3y – 20 = 0. Find the area bounded by these lines and x-axis.
Ans. We are given, 4x – 3y + 4 = 0
We get, 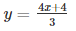
Now, substituting x = 0 in 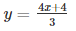 , we get
, we get
Substituting x = -I in 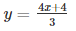
we get y =0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| x | 0 | -1 |
| y | 4/3 | 0 |
Plotting E(0, 4/3) and A (-1, 0) on the graph and by joining the points, we obtain the graph of equation
4x – 3y + 4 = 0.
We are given, 4x + 3y – 20 = 0
We get,
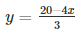
Now, substituting x = 0 in 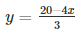 , we get
, we get
y = 7
Substituting x = 5 in 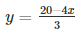 ,we get
,we get
y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 5 |
| Y | 20/3 | 0 |
Plotting D (0,20/3) and B(5,0) on the graph and by joining the points , we obtain the graph of equation 4x +3y – 20 = 0.
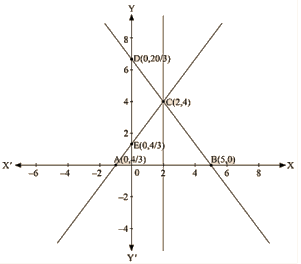
By the intersection of lines formed by 4x-3y + 4 = 0 and 4x+ 3y – 20 = 0 on the graph,
Triangle ABC is formed on x axis. Therefore, AB at x axis is the base of triangle ABC having AB = 6 units on x axis.
Draw CF perpendicular from C on x axis.
CF parallel to y axis is the height of triangle ABC having CF = 4 units on y axis.
Therefore, Area of triangle ABC, say A is given by
A = (Base x Height)/2
A = (AB x CF)/2
A = (6 x 4)/2
k = 12 sq. units
Q19 : The path of a train A is given by the equation 3x + 4y -12 = 0 and the path of another train B is given by the equation 6x + 8y – 48 = 0. Represent this situation graphically.
Ans. We are given the path of train A, 3x + 4y – 12 = 0
We get,
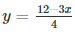
Now, substituting x = 0 in 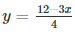 , we get
, we get
Y = 3
Substituting x = 4 in 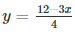 , we get
, we get
y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 4 |
| Y | 3 | 0 |
Plotting A(4,0) and E(0,3) on the graph and by joining the points , we obtain the graph of equation 3x+4y-12 = 0.
We are given the path of train B,
6x + 8y – 48 = 0
We get, 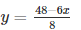
Now, substituting x = 0 in 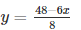 ,we get
,we get
y = 6
Substituting x = 8 in 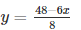 ,we get
,we get
y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 8 |
| Y | 6 | 0 |
Plotting C(0,6) and D(8,0) on the graph and by joining the points , we obtain the graph of equation 6x+8y-48 = 0
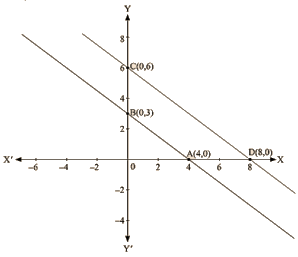
Q 20 : Ravish tells his daughter Aarushi, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be”. If present ages of Aarushi and Ravish are x and y years respectively, represent this situation algebraically as well as graphically.
Ans. We are given the present age of Ravish as y years and Aarushi as x years.
Age of Ravish seven years ago = y – 7
Age of Aarushi seven years ago = x – 7
It has already been said by Ravish that seven years ago he was seven times old then Aarushi was then
So, y – 7 = 7 (x – 7)
Y – 7 = 7 x – 49
7x – y = – 7 + 49
7x – y – 42 = 0 ——(1)
Age of Ravish three years from now = y + 3
Age of Aarushi three years from now = x+3
It has already been said by Ravish that three years from now he will be three times older then Aarushi will be then So,
Y + 3 = 3 (x + 3)
y + 3 = 3x + 9
3x + 9 – y – 3 = 0
3x – y + 6 = 0 —–(2)
(1) and (2) are the algebraic representation of the given statement.
We are given,
7x – y- 42 = 0
We get,
Y = 7x – 42
Now, substituting x = 0 in y = 7x —42,
we get y = -42
Substituting x = 6 in y = 7x – 42,
we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 6 |
| Y | -42 | 0 |
We are given,
3x – y + 6 =0
We get,
Y = 3x + 6
Now, substituting x=0 in y = 3x + 6,
We get y = 6
Substituting x= —2 in y = 3x + 6,
We get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | -2 |
| Y | 6 | 0 |
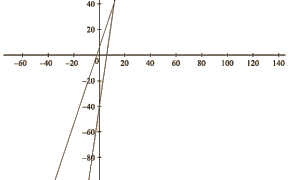
The red -line represents the equation 7x—y-42 =0.
The blue-line represents the equation 3x —y +6 =0.
Q21: Aarushi was driving a car with uniform speed of 60 km/h. Draw distance-time graph From the graph, find the distance travelled by Aarushi in
(i) 212 Hours
(ii) 12 Hour
Ans. Aarushi is driving the car with the uniform speed of 60 km/h. We represent time on X-axis and distance on Y-axis Now, graphically
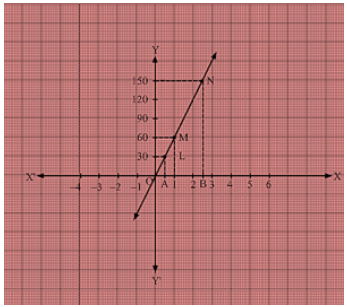
We are given that the car is travelling with a uniform speed 60 km/hr. This means car travels 60 km distance each hour. Thus the graph we get is of a straight line.
Also, we know when the car is at rest, the distance travelled is 0 km, speed is 0 km/hr and the time is also 0 hr. Thus, the given straight line will pass through O (0 , 0) and M (1, 60).
Join the points 0 and M and extend the line in both directions.
Now, we draw a dotted line parallel to y-axis from x = 12 that meets the straight line graph at L from which we draw a line parallel to x-axis that crosses y-axis at 30. Thus, in 12hr, distance travelled by the car is 30 km.
Now, we draw a dotted line parallel to y-axis from x = 212 that meets the straight line graph at N from which we draw a line parallel to x-axis that crosses y-axis at 150. Thus, in 212hr, distance travelled by the car is 150 km.
(i) Distance = Speed x Time Distance travelled in 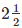 hours is given by
hours is given by
Distance=60 x 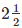
Distance = 60 x 5/2
Distance = 150 Km
(ii) Distance = Speed x Time Distance travelled in 12 hour is given by
Distance=60 x 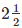
Distance = 30 km
FAQs on RD Sharma Solutions Ex-13.3, (Part -3), Linear Equation In Two Variables, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are linear equations in two variables? |  |
| 2. How can linear equations in two variables be solved? |  |
| 3. Can linear equations in two variables have multiple solutions? |  |
| 4. What is the importance of linear equations in two variables? |  |
| 5. Are linear equations in two variables limited to straight lines? |  |


















