NCERT Solutions for Class 8 Maths Chapter 10 - Ex 10.4 and 10.5 Practical Geometry- 2
Exercise 10.4
Question 1:
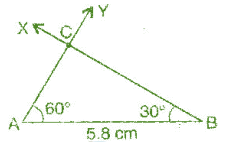
Construct ΔABC, given m∠A = 60:, m∠B = 30° and AB = 5,8 cm.
Answer 1:
To construct: ΔABC, given m∠A = 60:, m∠B = 30° and AB = 5,8 cm.
Steps of construction:
(a) Draw a line segment AB = 5.8 cm.
(b) At point A, draw an angle Z YAB = 6ti= with the help of a compass.
(c) At point B, draw Z XBA = 30" with the help of a compass.
(d) AY and BX intersect at the point C.
It is the required triangle ABC
Question 2:
Construct Δ PQR if PQ = 5 cm, m∠PQR = 105° and m∠.QRP = 40°.
Answer 2:
Given:
m∠ PQR = 105° and m∠ QRP = 40°
We know that sum of angles of a triangle is 180°.
∴ m∠PQR + m∠QRP + m∠ QPR = 180°
⇒ 105° + 40° + m∠QPR= 180°
⇒ 145° + m∠QPR= 180°
⇒ m∠QPR= 180° - 145°
⇒ m∠QPR = 35°
To construct: ΔPQR where m∠P = 35°, m∠Q = 105° and PQ = 5 cm.
Steps of construction:
(a) Draw a line segment PQ = 5 cm,
(b) At point P, draw ∠ XPQ = 35° with the help of protractor.
(c) At point Q, draw ∠ YQP = 105° with the help of protractor.
(d) XP and YQ intersect at point R.
It is the required triangle PQR.
Question 3:
Examine whether you can construct ΔDEF such that EF = 7.2 cm, m∠ E= 110° and m∠F
= 80°. Justify your answer.
Answer 3:
Given: In ΔDEF, m∠E = 110° and m∠T = 80°
Using angle sum property of triangle
∠D + ∠E + ∠F = 180°
⇒∠D + 110°+ 80° = 180°
⇒ ∠D + 190° = 180°
⇒ ∠D = 180° - 190° = -10°
Which is not possible.
Exercise 10.5
Question 1:
A right angled triangle PQR where m∠Q = 9ff, QR= 8 cm and PQ = 10 cm.
Answer 1:
To construct: Construct the right angled Δ PQR, where m∠Q = 90", QR = 8 cm and PR = 10 cm.
Steps of construction:
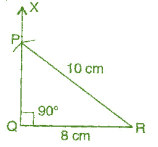
(a) Draw a line segment QR = 8 cm,
(b) At point Q, draw QX ⊥ QR,
(c) Taking R as centre, draw an arc of radius 10 cm.
(d) This arc cuts QX at point P.
(e) foin PQ.
It is the required right-angled triangle PQR,
Question 2:
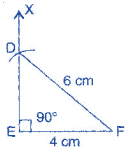
Construct a right-angled triangle whose hypotenuse is 6 cm long and one the legs is 4 cm long.
Answer 2:
To construct: A right-angled triangle DEF where DF = 6 cm and EF = 4 cm
Steps of construction:
(a) Draw a line segment EF = 4 cm.
(b) At point Q, draw EX ⊥ EF.
(c) Taking F as centre and radius 6 cm, draw an arc. (Hypotenuse)
(d) This arc cuts the EX at point D.
(e) Join DF.
It is the required right-angled triangle DEF.
Question 3:
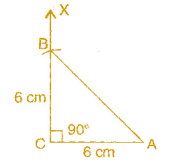
Construct an isosceles right angled triangle ABC, where m∠ACB = 90° and AC = 6 cm.
Answer 3:
To construct: An isosceles right angled triangle ABC where m∠ C = 90% AC = BC = 6 cm.
Steps of construction:
(a) Draw a line segment AC = 6 cm.
(b) At point C, draw XC ⊥ CA.
(c) Taking C as centre and radius 6 cm, draw an arc.
(d) This arc cuts CX at point B.
(e) Join BA.
It is the required isosceles right-angled triangle ABC.
Miscellaneous Questions
Questions:
Below are given the measures of certain sides and angles of triangles. Identify those which cannot be constructed and say why you cannot construct them. Construct rest of the triangle.
| Triangle | Given measurements | |||
1. | ΔABC | m∠A = 85° ; | m∠B = 115° ; | AB = 5 cm |
2. | ΔPQR | m∠ Q = 30° ; | m∠R = 60° ; | QR = 4.7 cm |
3. | ΔABC | m∠ A = 70° ; | m∠B = 50°; | AC = 3 cm |
4. | ΔLMN | m∠L = 60° ; | m∠N = 120° ; | LM = 5 cm |
5. | ΔABC | BC = 2 cm; | AB = 4 cm; | AC = 2 cm |
6. | ΔPQR | PQ = 3.5 cm; | QR = 4 cm; | PR = 3.5 cm |
7. | ΔXYZ | XY = 3 cm; | YZ = 4 cm; | XZ = 5 cm |
3. | ΔDEF | DE = 4.5 cm; | EF = 5.5 cm; | DF = 4 cm |
Answer 1:
In ΔABC, m∠A = 85o , m∠B = 115o , AB = 5 cm
Construction of ΔABC is not possible because m∠A = 85o + m∠B = 200o, and we know that the sum of angles of a triangle should be 180o.
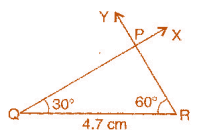
Answer 2:
To construct: ΔPQR where m∠Q = 30o , m∠R = 60o and QR = 4.7 cm.
Steps of construction:
(a) Draw a line segment QR = 4.7 cm.
(b) At point Q, draw ∠XQR = 30' with the help of a compass.
(c) At point R, draw ∠YRQ = 60' with the help of a compass.
(d) QX and RY intersect at point P.
It is the required triangle PQR.
Answer 3:
We know that the sum of angles of a triangle is 180°.
m∠ A + m∠B + m∠C = 180°
∴ 70° + 50° + m∠C = 180°
⇒ 120° + m∠C = 180°
⇒ m∠C = 180° - 120°
⇒ m∠C = 60°
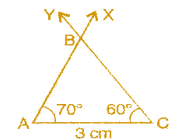
To construct: ΔABC where m∠A = 70°, m∠C = 60° and AC = 3 cm.
Steps of construction:
(a) Draw a line segment AC = 3 cm.
(b) At point C, draw ∠YCA = 60°.
(c) At point A, draw ∠XAC = 70°
(d) Rays XA and YC intersect at point B
It is the required triangle ABC.
Answer 4:
In ΔLMN , m∠L - 60° m∠N = 120°, LM = 5 cm
This ΔLMN is not possible to construct because m∠L + m∠N = 60° + 120° = 180° which forms a linear pair.
Answer 5:
Δ ABC, BC = 2 cm, AB = 4 cm and AC = 2 cm
This Δ ABC is not possible to construct because the condition is
Sum of lengths of two sides of a triangle should be greater than the third side.
AB< BC + AC
⇒ 4 < 2 + 2
⇒ 4 = 4,
Answer 6:
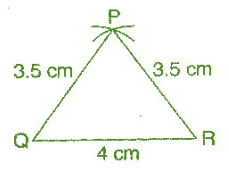
To construct: ΔPQR where PQ = 3.5 cm, QR = 4 cm and PR = 3.5 cm
Steps of construction:
(a) Draw a line segment QR = 4 cm.
(b) Taking Q as centre and radius 3.5 cm, draw an arc.
(c) Similarly, taking R as centre and radius 3.5 cm, draw another arc which intersects the first arc at point P.
it is the required triangle QPR.
Answer 7:
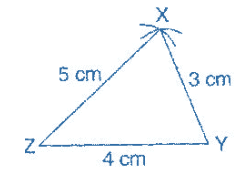
To construct: A triangle whose sides are XY = 3 cm, YZ = 4 cm and XZ = 5 cm.
Steps of construction:
(a) Draw a line segment ZY = 4 cm.
(b) Taking Z as center and radius 5 cm, draw an arc.
(c) Taking Y as centre and radius 3 cm, draw another arc.
(d) Both arcs intersect at point X.
It is the required triangle XYZ.
Answer 8:
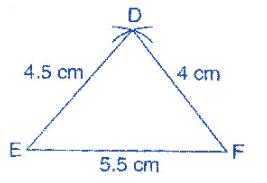
To construct: A triangle DEF whose sides are DE = 4.5 cm, EF = 5.5 cm and DF = 4 cm.
Steps of construction:
(a) Draw a line segment EF = 5.5 cm.
(b) Taking E as center and radius 4.5 cm, draw an arc.
(c) Taking F as center and radius 4 cm, draw another arc which intersects the first arc at point D.
It is the required triangle DEF.
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 8 Maths Chapter 10 - Ex 10.4 and 10.5 Practical Geometry- 2
| 1. What are the basic tools required for practical geometry? |  |
| 2. How can I construct an equilateral triangle using a compass and ruler? |  |
| 3. What is the difference between a line segment and a ray in geometry? |  |
| 4. How can I construct a perpendicular bisector of a line segment? |  |
| 5. How can I construct a triangle when its base, altitude, and one angle are given? |  |






















