NCERT Solutions Class 11 Maths Chapter 8 - Sequence And Series
Q1: Find the 20th and nthterms of the G.P.
Ans: The given G.P. is 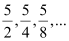
Here, a = First term = 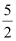
r = Common ratio = 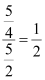
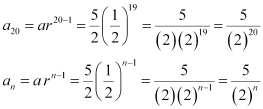
Q2: Find the 12th term of a G.P. whose 8th term is 192 and the common ratio is 2.
Ans: Common ratio, r = 2
Let a be the first term of the G.P.
∴ a8 = ar 8–1 = ar7
⇒ ar7 = 192
a(2)7 = 192
a(2)7 = (2)6 (3)
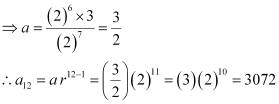
Q3: The 5th, 8th and 11th terms of a G.P. are p, q and s, respectively. Show that q2 = ps.
Ans: Let a be the first term and r be the common ratio of the G.P.
According to the given condition,
a5 = a r5–1 = a r4 = p … (1)
a8 = a r8–1 = a r7 = q … (2)
a11 = a r11–1 = a r10 = s … (3)
Dividing equation (2) by (1), we obtain

Dividing equation (3) by (2), we obtain

Equating the values of r3 obtained in (4) and (5), we obtain
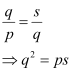
Thus, the given result is proved.
Q4: The 4th term of a G.P. is square of its second term, and the first term is –3. Determine its 7th term.
Ans: Let a be the first term and r be the common ratio of the G.P.
∴ a = –3
It is known that, an = arn–1
∴ a4 = ar3 = (–3) r3
a2 = a r1 = (–3) r
According to the given condition,
(–3) r3 = [(–3) r]2
⇒ –3r3 = 9 r2
⇒ r = –3
a7 = a r 7–1 = a r6 = (–3) (–3)6 = – (3)7 = –2187
Thus, the seventh term of the G.P. is –2187.
Q5: Which term of the following sequences:
(a) 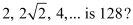
(b) 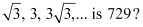
(c) 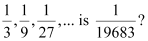
Ans: (a) The given sequence is 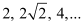
Here, a = 2 and r = 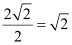
Let the nth term of the given sequence be 128.
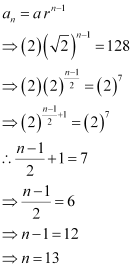
Thus, the 13th term of the given sequence is 128.
(b) The given sequence is 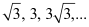
Here, 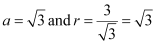
Let the nth term of the given sequence be 729.
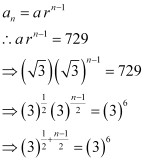
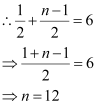
Thus, the 12th term of the given sequence is 729.
(c) The given sequence is 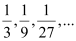
Here, 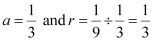
Let the nth term of the given sequence be 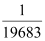 .
.
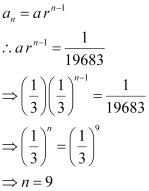
Thus, the 9th term of the given sequence is 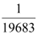 .
.
Q6: For what values of x, the numbers 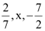 are in G.P?
are in G.P?
Ans: The given numbers are 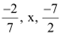 .
.
Common ratio = 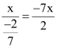
Also, common ratio = 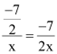
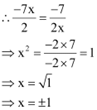
Thus, for x = ± 1, the given numbers will be in G.P.
Q7: Find the sum to 20 terms in the geometric progression 0.15, 0.015, 0.0015 …
Ans: The given G.P. is 0.15, 0.015, 0.00015, …
Here, a = 0.15 and 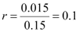
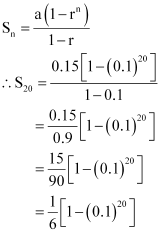
Q8: Find the sum to n terms in the geometric progression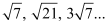
Ans: The given G.P. is 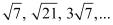
Here, 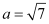
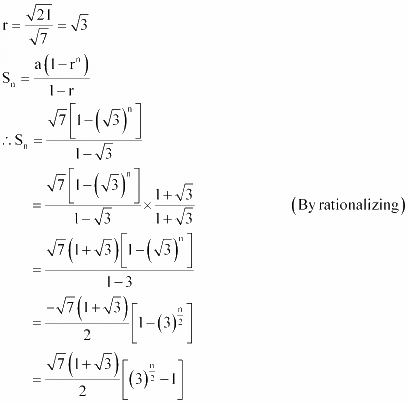
Q9: Find the sum to n terms in the geometric progression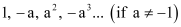
Ans: The given G.P. is 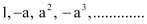
Here, first term = a1 = 1
Common ratio = r = – a
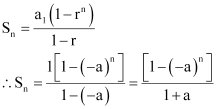
Q10: Find the sum to n terms in the geometric progression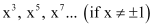
Ans: The given G.P. is 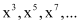
Here, a = x3 and r = x2

Q11: Evaluate 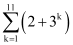
Ans:
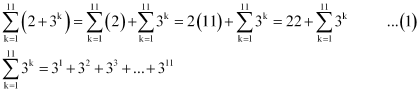
The terms of this sequence 3, 32, 33, … forms a G.P.
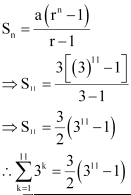
Substituting this value in equation (1), we obtain
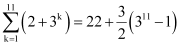
Q12: The sum of first three terms of a G.P. is 39/10 & their product is 1. Find the common ratio and the terms.
Ans: Let 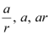 be the first three terms of the G.P.
be the first three terms of the G.P.
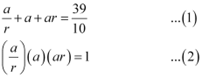
From (2), we obtain
a3 = 1
⇒ a = 1 (Considering real roots only)
Substituting a = 1 in equation (1), we obtain
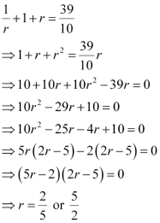
Thus, the three terms of G.P. are 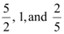 .
.
Q13: How many terms of G.P. 3, 32, 33, … are needed to give the sum 120?
Ans: The given G.P. is 3, 32, 33, …
Let n terms of this G.P. be required to obtain the sum as 120.
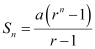
Here, a = 3 and r = 3
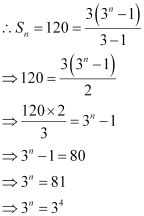
∴ n = 4
Thus, four terms of the given G.P. are required to obtain the sum as 120.
Q14: The sum of first three terms of a G.P. is 16 and the sum of the next three terms is 128. Determine the first term, the common ratio and the sum to n terms of the G.P.
Ans: Let the G.P. be a, ar, ar2, ar3, …
According to the given condition,
a + ar + ar2 = 16 and ar3 + ar4 + ar5 = 128
⇒ a (1 + r + r2) = 16 … (1)
ar3(1 + r + r2) = 128 … (2)
Dividing equation (2) by (1), we obtain
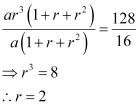
Substituting r = 2 in (1), we obtain
a (1 +2 +4) = 16
⇒ a (7) = 16
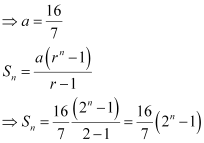
Q15: Given a G.P. with a = 729 and 7th term 64, determine S7.
Ans: a = 729
a7 = 64
Let r be the common ratio of the G.P.
It is known that, an = a rn–1
a7 = ar7–1 = (729)r6
⇒ 64 = 729 r6
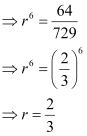
Also, it is known that, 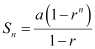
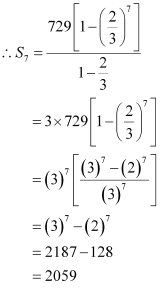
Q16: Find a G.P. for which sum of the first two terms is –4 and the fifth term is 4 times the third term.
Ans: Let a be the first term and r be the common ratio of the G.P.
According to the given conditions,
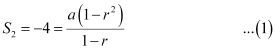
a5 = 4 × a3
ar4 = 4ar2
⇒ r2 = 4
∴ r = ± 2
From (1), we obtain
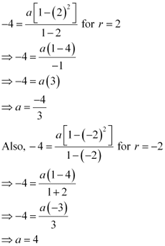
Thus, the required G.P. is
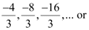 4, –8, 16, –32, …
4, –8, 16, –32, …
Q17: If the 4th, 10th and 16th terms of a G.P. are x, y and z, respectively. Prove that x, y, z are in G.P.
Ans: Let a be the first term and r be the common ratio of the G.P.
According to the given condition,
a4 = a r3 = x … (1)
a10 = a r9 = y … (2)
a16 = a r15 = z … (3)
Dividing (2) by (1), we obtain
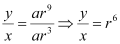
Dividing (3) by (2), we obtain
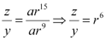
∴ 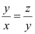 Thus, x, y, z are in G. P.
Thus, x, y, z are in G. P.
Q18: Find the sum to n terms of the sequence, 8, 88, 888, 8888…
Ans: The given sequence is 8, 88, 888, 8888…
This sequence is not a G.P. However, it can be changed to G.P. by writing the terms as
Sn = 8+ 88+ 888+ 8888 …………….. to n terms
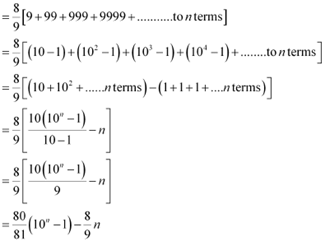
Q19: Find the sum of the products of the corresponding terms of the sequences 2, 4, 8, 16, 32 and 128, 32, 8, 2, ½ .
Ans Required sum = 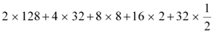
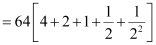
Here, 4, 2, 1, 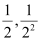 is a G.P.
is a G.P.
First term, a = 4
Common ratio, r = 
It is known that, 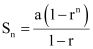
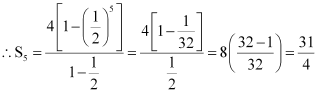
∴ Required sum = 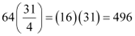
Q20: Show that the products of the corresponding terms of the sequences 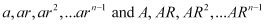 form a G.P, and find the common ratio.
form a G.P, and find the common ratio.
Ans: It has to be proved that the sequence, aA, arAR, ar2AR2, …arn–1ARn–1, forms a G.P.
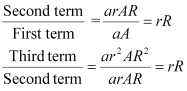
Thus, the above sequence forms a G.P. and the common ratio is rR.
Q21: Find four numbers forming a geometric progression in which third term is greater than the first term by 9, and the second term is greater than the 4th by 18.
Ans: Let a be the first term and r be the common ratio of the G.P.
a1 = a, a2 = ar, a3 = ar2, a4 = ar3
By the given condition,
a3 = a1+ 9
⇒ ar2 = a + 9 … (1)
a2 = a4 + 18
⇒ ar = ar3 + 18 … (2)
From (1) and (2), we obtain
a(r2 – 1) = 9 … (3)
ar (1– r2) = 18 … (4)
Dividing (4) by (3), we obtain
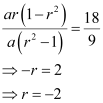
Substituting the value of r in (1), we obtain
4a = a+ 9
⇒ 3a = 9
∴ a = 3
Thus, the first four numbers of the G.P. are 3, 3(– 2), 3(–2)2, and 3(–2)3 i.e., 3¸–6, 12, and –24.
Q22: If the 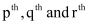 terms of a G.P. are a, b and c, respectively. Prove that
terms of a G.P. are a, b and c, respectively. Prove that 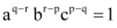
Ans: Let A be the first term and R be the common ratio of the G.P.
According to the given information,
ARp–1 = a
ARq–1 = b
ARr–1 = c
aq–r br–p cp–q
= Aq–r × R(p–1) (q–r) × Ar–p × R(q–1) (r-p) × Ap–q × R(r –1)(p–q)
= Aq – r + r – p + p – q × R (pr – pr – q + r) (rq – r + p – pq) (pr – p – qr + q)
= A0 × R0
= 1
Thus, the given result is proved.
Q23: If the first and the nth term of a G.P. are a ad b, respectively, and if P is the product of n terms, prove that P2 = (ab)n.
Ans: The first term of the G.P is a and the last term is b.
Therefore, the G.P. is a, ar, ar2, ar3, … arn–1, where r is the common ratio.
b = arn–1 … (1)
P = Product of n terms
= (a) (ar) (ar2) … (arn–1)
= (a × a ×…a) (r × r2 × …rn–1)
= an r 1 +2 …(n–1) … (2)
Here, 1, 2, …(n – 1) is an A.P.
∴ 1+ 2 ………. +(n – 1) 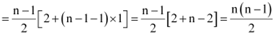
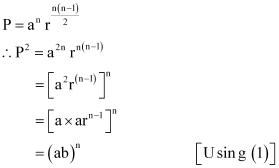
Q24: Show that the ratio of the sum of first n terms of a G.P. to the sum of terms from 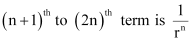
Ans: Let a be the first term and r be the common ratio of the G.P.
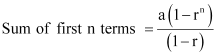
Since there are n terms from (n + 1)th to (2n)th term,
Sum of terms from(n + 1)th to (2n)th term 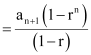
a n+ 1 = ar n+ 1 – 1 = arn
Thus, required ratio = 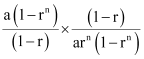
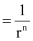
Thus, the ratio of the sum of first n terms of a G.P. to the sum of terms from (n + 1)th to (2n)th term is 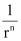 .
.
Q25: If a, b, c and d are in G.P. show that 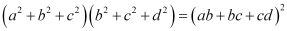 .
.
Ans: a, b, c, d are in G.P.
Therefore,
bc = ad … (1)
b2 = ac … (2)
c2 = bd … (3)
It has to be proved that,
(a2 + b2 + c2) (b2+ c2 + d2) = (ab + bc – cd)2
R.H.S.
= (ab + bc+ cd)2
= (ab + ad + cd)2 [Using (1)]
= [ab + d (a + c)]2
= a2b2 + 2abd (a + c) + d2 (a + c)2
= a2b2 + 2a2bd+ 2acbd + d2(a2 + 2ac + c2)
= a2b2 + 2a2c2+ 2b2c2 + d2a2 + 2d2b2 + d2c2 [Using (1) and (2)]
= a2b2 + a2c2 + a2c2 + b2c2 + b2c2 + d2a2 + d2b2 + d2b2 + d2c2
= a2b2 + a2c2 + a2d2 + b2 × b2 + b2c2+ b2d2 + c2b2 + c2 × c2 + c2d2
[Using (2) and (3) and rearranging terms]
= a2(b2 + c2 + d2) +b2 (b2 + c2 + d2) + c2 (b2 + c2 + d2)
= (a2 + b2 + c2) (b2 + c2 + d2)
= L.H.S.
∴ L.H.S. = R.H.S.
∴ 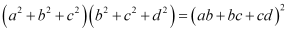
Q26: Insert two numbers between 3 and 81 so that the resulting sequence is G.P.
Ans: Let G1 and G2 be two numbers between 3 and 81 such that the series, 3, G1, G2, 81, forms a G.P.
Let a be the first term and r be the common ratio of the G.P.
∴ 81 = (3) (r)3
⇒ r3 = 27
∴ r = 3 (Taking real roots only)
For r = 3,
G1 = ar = (3) (3) = 9
G2 = ar2 = (3) (3)2 = 27
Thus, the required two numbers are 9 and 27.
Q27: Find the value of n so that 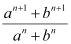 may be the geometric mean between a and b.
may be the geometric mean between a and b.
Ans: G. M. of a and b is 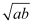 .
.
By the given condition, 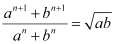
Squaring both sides, we obtain
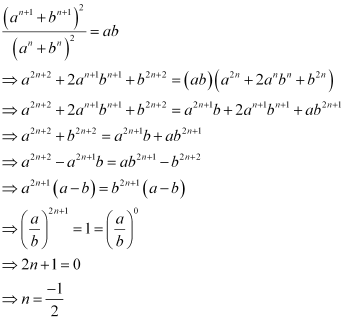
Q28: The sum of two numbers is 6 times their geometric mean, show that numbers are in the ratio 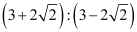 .
.
Ans: Let the two numbers be a and b.
G.M. = 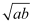
According to the given condition,
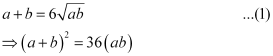
Also,
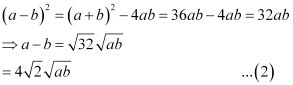
Adding (1) and (2), we obtain
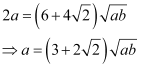
Substituting the value of a in (1), we obtain
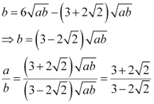
Thus, the required ratio is 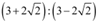 .
.
Q29: If A and G be A.M. and G.M., respectively between two positive numbers, prove that the numbers are .
.
Ans: It is given that A and G are A.M. and G.M. between two positive numbers. Let these two positive numbers be a and b.

From (1) and (2), we obtain
a + b = 2A … (3)
ab = G2 … (4)
Substituting the value of a and b from (3) and (4) in the identity (a – b)2 = (a + b)2 – 4ab, we obtain
(a – b)2 = 4A2 – 4G2 = 4 (A2–G2)
(a – b)2 = 4 (A + G) (A – G)
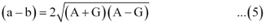
From (3) and (5), we obtain
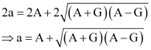
Substituting the value of a in (3), we obtain
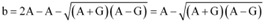
Thus, the two numbers are 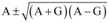 .
.
Q30: The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour?
Ans: It is given that the number of bacteria doubles every hour. Therefore, the number of bacteria after every hour will form a G.P.
Here, a = 30 and r = 2
∴ a3 = ar2 = (30) (2)2 = 120
Therefore, the number of bacteria at the end of 2nd hour will be 120.
a5 = ar4 = (30) (2)4 = 480
The number of bacteria at the end of 4th hour will be 480.
an + 1 = arn = (30) 2n
Thus, number of bacteria at the end of nth hour will be 30(2)n.
Q31: What will Rs 500 amounts to in 10 years after its deposit in a bank which pays annual interest rate of 10% compounded annually?Ans: The amount deposited in the bank is Rs 500.
At the end of first year, amount = 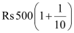 = Rs 500 (1.1)
= Rs 500 (1.1)
At the end of 2nd year, amount = Rs 500 (1.1) (1.1)
At the end of 3rd year, amount = Rs 500 (1.1) (1.1) (1.1) and so on
∴ Amount at the end of 10 years = Rs 500 (1.1) (1.1) … (10 times)
= Rs 500(1.1)10
Q32: If A.M. and G.M. of roots of a quadratic equation are 8 and 5, respectively, then obtain the quadratic equation.
Ans: Let the root of the quadratic equation be a and b.
According to the given condition,
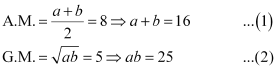
The quadratic equation is given by,
x2– x (Sum of roots) + (Product of roots) = 0
x2 – x (a + b) + (ab) = 0
x2 – 16x + 25 = 0 [Using (1) and (2)]
Thus, the required quadratic equation is x2 – 16x + 25 = 0
|
73 videos|264 docs|91 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 8 - Sequence And Series
| 1. What is the difference between a sequence and a series in mathematics? |  |
| 2. How do you find the nth term of a sequence? |  |
| 3. What is the formula for the sum of an arithmetic series? |  |
| 4. How do you determine if a series is convergent or divergent? |  |
| 5. What is the difference between an arithmetic series and a geometric series? |  |

















