RD Sharma Solutions (Ex 1.1): Rational Numbers | Mathematics (Maths) Class 8 PDF Download
Q.1. Add the following rational numbers.
(i) 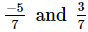
(ii)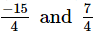
(iii)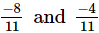
(iv)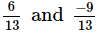
Ans.
(i)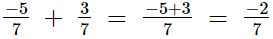
(ii) 
(iii) 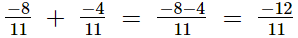
(iv) 
Q.2. Add the following rational numbers:
(i)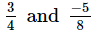
(ii)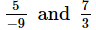
(iii)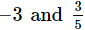
(iv)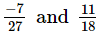
(v)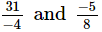
(vi)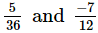
(vii)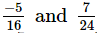
(viii)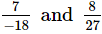
Ans.
(i) Clearly, denominators of the given numbers are positive. The L.C.M. of denominators 4 and 8 is 8.
Now, we will express 34 in the form in which it takes the denominator is 8.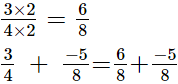
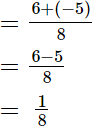
(ii)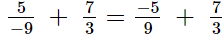
The L.C.M. of denominators 9 and 3 is 9.
Now, we will express 7/3 in the form in which it takes the denominator is 9.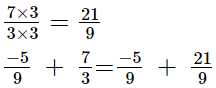
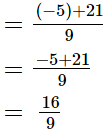
(iii)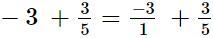
The L.C.M. of denominators 1 and 5 is 5.
Now, we will express −3/1 in the form in which it takes the denominator 5.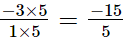
So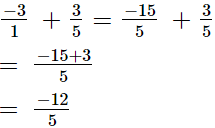
(iv)
The L.C.M. of denominators 27 and 18 is 54.
Now, we will express 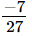 and
and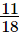 in the form in which they take the denominator 54.
in the form in which they take the denominator 54.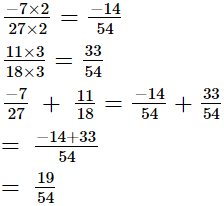
(v)
We have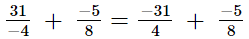
The L.C.M. of denominators 4 and 8 is 8.
Now, we will express 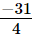 in the form in which it takes the denominator 8.
in the form in which it takes the denominator 8.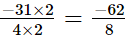
So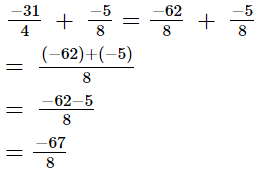
(vi)
The L.C.M. of denominators 36 and 12 is 36.
Now, we will express 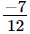 in the form in which it takes the denominator 36.
in the form in which it takes the denominator 36.
So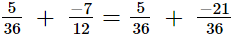

The L.C.M. of denominators 16 and 24 is 48.
Now, we will express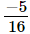 and
and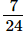 in the form in which they take the denominator 48.
in the form in which they take the denominator 48.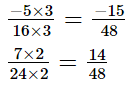
So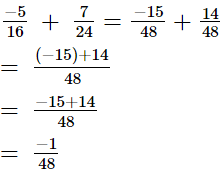
(viii)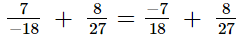
The L.C.M. of denominators 18 and 27 is 54.
Now, we will express 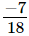 and
and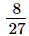 in the form in which they take the denominator 54.
in the form in which they take the denominator 54.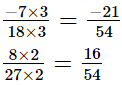
So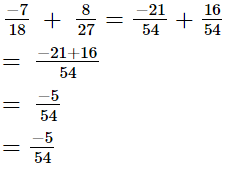
Q.3. Simplify:
(i)
(ii)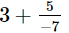
(iii)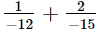
(iv)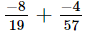
(v)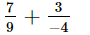
(vi)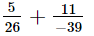
(vii)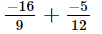
(viii)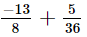
(ix)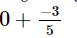
(x)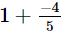
Ans:
(i) 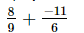
L.C.M. of the denominators 9 and 6 is 18.
Now, we will express 8/9 and −11/6 in the form in which they take the denominator 18.
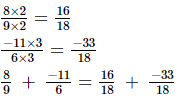
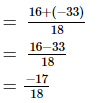
(ii) 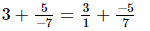
L.C.M. of the denominators 1 and 7 is 7.
Now, we will express 3/1 in the form in which it takes the denominator 7.
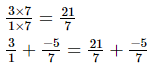
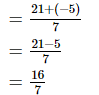
(iii) 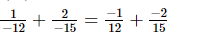
L.C.M. of the denominators 12 and 15 is 60.
Now, we will express −1/12 and −2/15 in the form in which they take the denominator 60.
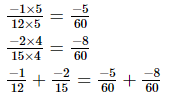
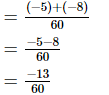
(iv) 
L.C.M. of the denominators 19 and 57 is 57.
Now, we will express −8/19 in the form in which it takes the denominator 57.
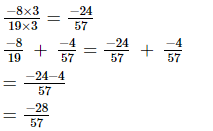
(v) 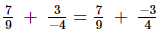
Now, we will express 7/9 and −3/4 in the form in which they take the denominator 36.

So,
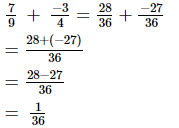
(vi) 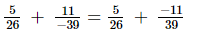
L.C.M. of the denominators 26 and 39 is 78.
Now, we will express 5/26 and −1/139 in the form in which they take the denominator 78.
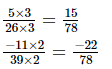
So,
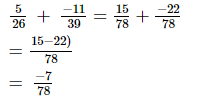
(vii) 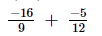
L.C.M. of the denominators 9 and 12 is 36.
Now, we will express −16/9 and −5/12 in the form in which they take the denominator 36.
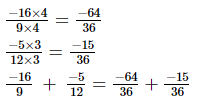
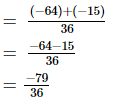
(viii) 
L.C.M. of the denominators 8 and 36 is 72.
Now, we will express −13/8 and 5/36 in the form in which they take the denominator 72.
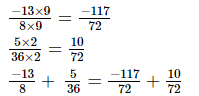
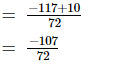
(ix) 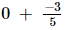
Taking L.C.M. of the denominator:
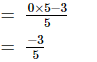
(x) 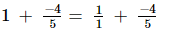
L.C.M. of the denominators 1 and 5 is 5.
Now, we will express 1/1 in the form in which it takes the denominator 5.
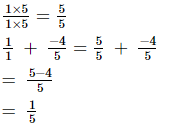
Q.4. Add and express the sum as a mixed fraction:
(i)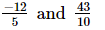
(ii)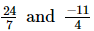
(iii)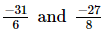
(iv)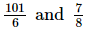
Ans:
(i)
We have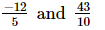
L.C.M. of the denominators 5 and 10 is 10.
Now, we will express −12/5 in the form in which it takes the denominator 10.
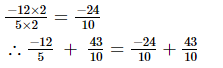
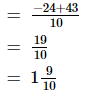
(ii)
We have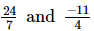
L.C.M. of the denominators 7 and 4 is 28.
Now, we will express 24/7 and −1/14 in the form in which they take the denominator 28.
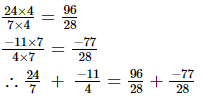
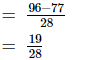
(iii)
We have 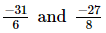
L.C.M. of the denominators 6 and 8 is 24.
Now, we will express −31/6 and −27/8 in the form in which they take the denominator 24.

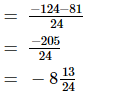
(iv)
We have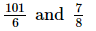
L.C.M. of the denominators 6 and 8 is 24.
Now, we will express 101/6 and 7/8 in the form in which they take the denominator 24.
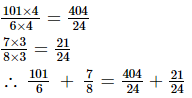
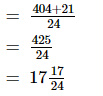
|
79 videos|408 docs|31 tests
|
FAQs on RD Sharma Solutions (Ex 1.1): Rational Numbers - Mathematics (Maths) Class 8
| 1. What are rational numbers? |  |
| 2. How can we determine if a number is rational or not? |  |
| 3. Can every fraction be considered a rational number? |  |
| 4. Are whole numbers and integers also rational numbers? |  |
| 5. Can irrational numbers be expressed as fractions? |  |



















