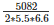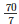Ex-18.1(Part - 2), Surface Area And Volume Of A Cuboid And Cube, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q11) The dimensions of a rectangular box are in the ratio of 2 : 3 : 4 and the difference between the cost of covering it with a sheet of paper at the rates of Rs 8 and Rs 9.50 per m2 is Rs 1248. Find the dimensions of the box.
Solution:
Let the ratio be ‘x’
Length (l) = 2x
Breadth (b) = 3x
Height (h) = 4x
Therefore, Total Surface area = 2[lb+bh+hl]
= 2(6x2+12x2+8x2)
= 52x2m2
When the cost is at Rs.8 per m2
Therefore, the total cost of 52x2 = 8∗52x2
= Rs. 416x2
Taking the cost at Rs. 9.5 per m2,
Total cost of 52x2m2 = 9.5∗52x2
= Rs. 494x2
Therefore, the Difference in cost = Rs. 494x2– Rs. 416x2
- 1248 = Rs. 78x2
- x2 =

- x2 = 16
- x = 4
Q12) A closed iron tank 12 m long, 9 m wide and 4 m deep is to be made. Determine the cost of iron sheet used at the rate of Rs 5 per meter sheet, a sheet being 2 m wide.
Solution:
Length (l) = 12m
Breadth (b) = 9m
Height (h) = 4m
Total surface area of the tank = 2[lb+bh+hl]
= 2[12*9+9*4+12*4]
= 2[108+36+48]
= 384m2
The Length of the Iron sheet = 
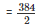
= 192m.
Cost of the Iron Sheet = Length of the Iron Sheet*Cost rate
= 192*5
= Rs. 960
Q13) Ravish wanted to make a temporary shelter for his car by making a box-like structure with the tarpaulin that covers all the four sides and the top of the car ( with the front face of a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how many tarpaulins would be required to make the shelter of height 2.5 m with base dimensions 4 m x 3m?
Solution:
Given That,
Shelter length = 4m
Breadth = 3m
Height = 2.5m
The tarpaulin will be required for top and four sides of the shelter.
The Area of tarpaulin required = 2h(l+b)+lb
⇒2∗2.5(4+3)+4∗3
⇒5(7)+12
⇒47m2
Q14) An open box is made of wood 3 cm thick. Its external length, breadth and height are 1.48m, 1.16 m and 8.3 dm. Find the cost of painting the inner surface of Rs 50 per sq. metre.
Solution:
Given Data:
Outer Dimensions
Length = 148cm
Breadth = 116cm
Height = 83cm
Inner Dimensions
Length = 148-(2*3) = 142cm
Breadth = 116-(2*3) = 110cm
Height = 83-3 = 80
Surface Area of the Inner region = 2h(l+b)+lb
= 2*80(142+110)+142*110
= 2*80*252+142*110
= 55940cm2
= 5.2904m2
Hence, the cost of Painting the Surface Area of the Inner region = 5.2904*50
= Rs. 279.70
Q15) The cost of preparing the walls of a room 12 m long at the rate of Rs 1.35 per square meter is Rs 340.20 and the cost of matting the floor at 85 paise per square meter is Rs 91.80. Find the height of the room.
Solution:
Given that,
Length of the room = 12m
Let the height of the room be ‘h’
Area of 4 walls = 2(l+b)*h
According to the question
- 2(l+b)*h*1.35 = 340.20
- 2(12+b0*h*1.35 = 340.20
- (12+b)*h =
 = 126 …..(1)
= 126 …..(1)
Also Area of the Floor = l*b
Therefore,l∗b∗0.85 = 91.80
⇒12∗b∗0.85 = 91.80
⇒b = 9m ……(2)
Substituting b = 9m in equation (1)
- (12+9)*h = 126 ; h = 6m
Q16) The dimensions of a room are 12.5 m by 9 m by 7 m. There are 2 doors and 4 windows in the room; each door measures 2.5 m by 1.2 m and each window 1.5 m by 1 m. Find the cost of painting the walls at Rs 3.50 per square meter.
Solution:
Given Length of the room = 12.5m
Breadth of the room = 9m
Height of the room = 7m
Therefore, total surface area of the four walls = 2(l+b)*h
= 2(12.5+9)*7
= 301 m2
Area of 2 doors = 2 (2.5*1.2)
= 6 m2
Area of 4 windows = 4 (1.5*1)
= 6 m2
Area to be painted on 4 walls = 301 – (6+6)
= 301 – 12
= 289 m2
Therefore, Cost of painting = 289*3.50
= Rs. 1011.5
Q17) The length and breadth of a hall are in the ratio 4 : 3 and its height is 5.5 meters. The cost of decorating its walls (including doors and windows) at Rs 6.60 per square meter is Rs 5082. Find the length and breadth of the room.
Solution:
Let the length be 4a and breadth be 3a
Height = 5.5m [Given]
As mentioned in the question, the cost of decorating 4 walls at the rate of Rs. 6.60 per m2 is Rs. 5082.
- Area of four walls * rate = Total cost of Painting
- 2(l+b)*h*6.6 = 5082
- 2(4a+3a)*5.5*6.6 = 5082
- 7a =

- 7a = 70
- a =

- a = 10
Length = 4a = 4*10 = 40m
Breadth = 3a = 3*10 = 30m
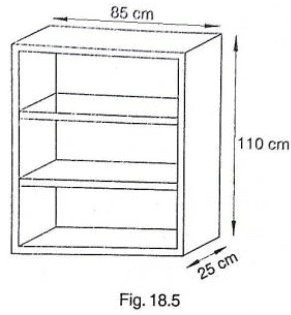
Q18) A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85cm (See figure 18.5). The thickness of the plank is 5cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2. Find the total expenses required for polishing and painting the surface of the bookshelf.
Solution:
External length of book shelf = 85cm
Breadth = 25cm
Height = 110cm
External surface area of shelf while leaving front face of shelf
- lh+2(lb+bh)
- [85*110+2(85*25+25*110)]
- 19100 cm2
Area of Front face = [85*110 – 75*100+2(75*5)] cm2
= 1850+750 cm2
= 2600 cm2
Area to be polished = 19100+2600 cm2
= 21700 cm2
Cost of polishing 1cm2 area = Rs. 0.20
Cost of polishing 21700cm2 area = 21700*0.20
= Rs. 4340
Now, Length(l), breadth(b), height(h) of each row of book shelf is 75cm, 20cm and 30cm =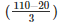 respectively
respectively
Area to be painted in 1 row = 2(l+h)b+lh
- [2(75+30)*20+75*30)] cm2
- (4200+2250) cm2
- 6450 cm2
Area to be painted in 3 rows = 3*6450
= Rs. 19350 cm2
Cost of painting 1cm2 area = Rs. 0.10
Cost of painting 19350cm2 area = 19350*0.10
= Rs.1935
Total expense required for polishing and painting the surface of the bookshelf = 4340+1935
= Rs.6275
Q19) The paint in a certain container is sufficient to paint on an area equal to 9.375 m2, How many bricks of dimension 22.5cm x 10cm x 7.5cm can be painted out of this container?
Solution:
The paint in the container can paint the area,
A = 9.375 m2
= 93750 cm2 [Since 1 m = 100 cm]
Dimensions of a single brick,
Length (l) = 22.5 cm
Breadth (b) = 10 cm
Height (h) = 7.5 cm
We need to find the number of bricks that can be painted.
Surface area of a brick
A’ = 2 (lb + bh + hl)
= 2 (22.5 * 10 + 10 * 7.5 + 7.5 * 22.5)
= 2 (225 + 75 + 168.75) = 937.50 cm2
Number of bricks that can be painted = 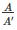
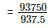 = 100
= 100
Hence 100 bricks can be painted out of the container.
FAQs on Ex-18.1(Part - 2), Surface Area And Volume Of A Cuboid And Cube, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the formula for finding the surface area of a cuboid? |  |
| 2. How do you calculate the volume of a cube? |  |
| 3. Can the surface area of a cuboid be greater than its volume? |  |
| 4. How can you find the length of the side of a cube if its volume is given? |  |
| 5. Can a cuboid have the same surface area as a cube? |  |

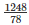
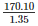 = 126 …..(1)
= 126 …..(1)