Chapter 18 - Practical Geometry (Constructions) (Part - 4), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 18.6:
Question 1:
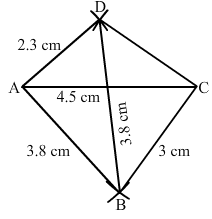
Construct a quadrilateral ABCD in which AB = 3.8 cm, BC = 3.0 cm, AD = 2.3 cm, AC = 4.5 cm and BD = 3.8 cm.
ANSWER:
Steps of construction:
Step I: Draw AC = 6 cm.
Step II: With A as the centre and radius 3.8 cm, draw an arc.
Step III : With C as the centre and radius 3.0 cm, draw an arc to intersect the arc drawn in Step II at B.
Step IV: With B as the centre and radius 3.8 cm, draw an arc on the other side of AC.
Step V :With A as the centre and radius 2.3 cm, draw an arc to intersect the arc drawn in Step IV at D.
Step VI: Join BA, DA, BC and CD to obtained the required quadrilateral.
Question 2:
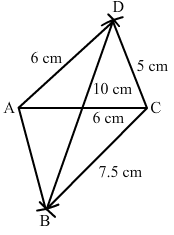
Construct a quadrilateral ABCD in which BC = 7.5 cm, AC = AD = 6 cm, CD = 5 cm and BD = 10 cm.
ANSWER:
Steps of construction:
Step I: Draw AC = 6 cm.
Step II: With A as the centre and radius 6 cm, draw an arc.
Step III : With C as the centre and radius 5 cm, draw an arc to intersect the arc drawn in Step II at D.
Step IV: With D as the centre and radius 10 cm, draw an arc on the other side of the line segment AC.
Step V :With C as the centre and radius 7.5 cm, draw an arc to intersect the arc drawn in Step IV at B.
Step VI: Join BA, DA, BC and CD to obtained the required quadrilateral.
Question 3:
Construct a quadrilateral ABCD, when AB = 3 cm, CD = 3 cm, DA = 7.5 cm, AC = 8 cm and BD = 4 cm.
ANSWER:
If we consider a triangle ABD from the given data, then
AB = 3 cm
BD = 4 cm
AD = 7.5 cm
AB + BD = 3 + 4 = 7 cm
However, we know that the sum of the lengths of two sides of a triangle is always greater than the third side.
Therefore, construction is not possible from the given data.
Question 4:
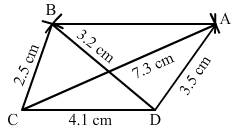
Construct a quadrilateral ABCD given AD = 3.5 cm, BC = 2.5 cm, CD = 4.1 cm, AC = 7.3 cm and BD = 3.2 cm.
ANSWER:
Steps of construction:
Step I: Draw CD = 4.1 cm.
Step II: With C as the centre and radius 7.3 cm, draw an arc.
Step III : With D as the centre and radius 3.5 cm, draw an arc to intersect the arc drawn in Step II at A.
Step IV: With D as the centre and radius 3.2 cm, draw an arc on the other side of AC.
Step V :With C as the centre and radius 2.5 cm, draw an arc to intersect the arc drawn in Step IV at B.
Step VI: Join BA, DA, BC and BD and AC to obtained the required quadrilateral.
Question 5:
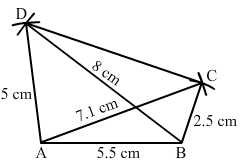
Construct a quadrilateral ABCD given AD = 5 cm, AB = 5.5 cm, BC = 2.5 cm, AC = 7.1 cm and BD = 8 cm.
ANSWER:
Steps of construction:
Step I: Draw AB = 5.5 cm.
Step II: With A as the centre and radius 7.1 cm, draw an arc.
Step III : With B as the centre and radius 2.5 cm, draw an arc to intersect the arc drawn in Step II at C.
Step IV: With B as the centre and radius 8 cm, draw an arc.
Step V :With A as the centre and radius 5 cm, draw an arc to intersect the arc drawn in Step IV at D.
Step VI: Join DA, DB, BC, AC and CD to obtained the required quadrilateral.
Question 6:
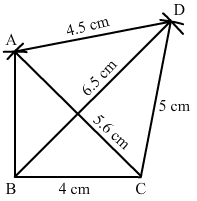
Construct a quadrilateral ABCD in which BC = 4 cm, CA = 5.6 cm, AD = 4.5 cm, CD = 5 cm and BD = 6.5 cm.
ANSWER:
Steps of construction:
Step I: Draw BC = 4 cm.
Step II: With B as the centre and radius 6.5 cm, draw an arc.
Step III : With C as the centre and radius 5 cm, draw an arc to intersect the arc drawn in Step II at D.
Step IV: With C as the centre and radius 5.6 cm, draw an arc on the same side.
Step V :With D as the centre and radius 4.5 cm, draw an arc to intersect the arc drawn in Step IV at A.
Step VI: Join BA, AC, DA, BD and CD to obtained the required quadrilateral.
FAQs on Chapter 18 - Practical Geometry (Constructions) (Part - 4), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What are the steps to construct a perpendicular bisector of a line segment? |  |
| 2. How can I construct a line parallel to a given line passing through a given point? |  |
| 3. How can I construct an angle of 60 degrees? |  |
| 4. Can I construct a triangle with any three given line segments? |  |
| 5. How can I construct an equilateral triangle? |  |
















