Class 9 Math: Sample Question Paper- 1 (With Solutions) PDF Download
| Table of contents |

|
| Class - IX |

|
| Mathematics |

|
| Time: 3 Hours |

|
| Maximum Marks: 80 |

|
| Section A |

|
| Section B |

|
| Section C |

|
| Section D |

|
Class - IX
Mathematics
Time: 3 Hours
Maximum Marks: 80
General Instructions:
- All questions are compulsory.
- The question paper consists of 30 questions divided into four sections A, B, C, and D. Section A comprises of 6 questions of 1 mark each, Section B comprises of 6 questions of 2 marks each, Section C comprises of 10 questions of 3 marks each and Section D comprises of 8 questions of 4 marks each.
- Use of a calculator is not permitted.
Section A
Q.1. Simplify: (5 + √5)(5 - √5)
Ans. (5 + √5)(5 - √5 ) = (5)2 - (√5)2 = 25 - 5 = 20 [∵ a2 - b2 = (a - b)(a + b)]
Q.2. Find the value of p such that (x – 1) is a factor of the polynomial x3 + 10x2 + px.
Ans. p(x) = x3 + 10x2 + px
(x – 1) is the factor of p(x)
∴ x – 1 = 0
∴ x = 1 will satisfy p(x)
► p(1) = 0
► (1)3 + 10(1)2 + p(1) = 0
► 1 + 10 + p = 0
► p = –11
Q.3. In ΔABC, ∠A = 100° and AB = AC. Find ∠B.
OR
Find the angles of an isosceles triangle whose equal angles and the non-equal angles are in the ratio 3:4.
Ans. Given, AB = AC
∴ ∠B = ∠C ...(1) (∵ angles opp. to equal sides are equal)
In ΔABC, we have ∠A + ∠B + ∠C = 180°
► ∠A + ∠B + ∠B = 180° ....[From (1)]
► 100° + 2∠B = 180° ....(∵∠A = 100°)
► 2∠B = 80°
► ∠B = 40°
OR
The equal angles and the non-equal angle are in the ratio 3 : 4.
Let equal angles be 3x each, therefore the non-equal angle is 4x.
Angles of a triangle = 180
► 3x + 3x + 4x = 180
► 10 x = 180
► x = 18
Therefore, 3x = 54 and 4x = 72
Angles are: 54, 54 and 72.
Q.4. The cost of the notebook is twice the cost of a pen. Write a linear equation in the two variables to represent this statement?
Ans. Let, the cost of a notebook = Rs. x
The cost of a pen = Rs. y
According to given statement, x = 2y
i.e. x – 2y = 0
Q.5. Find the range of data: 70, 65, 75, 71, 36, 55, 61, 62, 41, 40, 39, and 35.
OR
What is the class mark of the class interval 45 - 52?
Ans. Arranging the given data in Ascending order:
35, 36, 39, 40, 41, 55, 61, 62, 65, 70, 71, 75
∴ Range = Maximum value – Minimum value = 75 – 35 = 40
OR
The class mark of 45 - 52 is: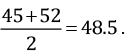
Q.6. In a parallelogram PQRS, What is the sum of ∠R and ∠S?
Ans. In a Parallelogram PQRS,
∠R and ∠S are consecutive interior angles on the same side of the transversal SR.
Therefore, ∠R + ∠S = 180°.
Section B
Q.7. Simplify: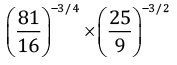
OR
Simplify: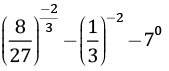
Ans. 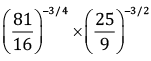
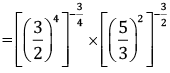
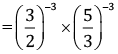
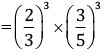
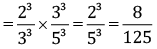
OR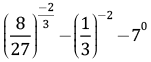
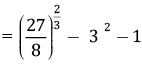
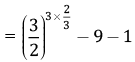
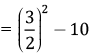
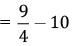
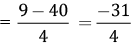
Q.8. Factorise: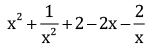
Ans.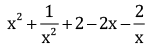
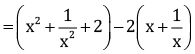
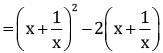
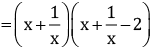
Q.9. Where do the following points lie?
(a) (–4, 0)
(b) (–10, 2)
(c) (0, 8)
(d) (10, 4)
Ans. (a) The point of the form (a, 0) lies on the x-axis.
So, the point (–4, 0) will lie on the negative side of the x-axis.
(b) (–, +) are the sign of the coordinate of points in the quadrant II.
So, the point (–10, 2) lies in the quadrant II.
(c) Point of the form (0, a) lie on the y-axis.
So, the point (0, 8) will lie on the positive side of the y-axis.
(d) (+, +) are the sign of the coordinates of points in the quadrant I.
So, the point (10, 4) lies in the quadrant I.
Q.10. In the given figure, ABCDE is a pentagon. A line through B and parallel to AC meets DC produced at F. Show that area(∆ACB) = area(∆ACF).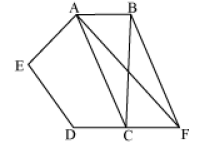 Ans. ∆ACB and ∆ACF lie on the same base AC and are between the same parallel lines AC and BF.
Ans. ∆ACB and ∆ACF lie on the same base AC and are between the same parallel lines AC and BF.
∴ area(∆ACB) = area(∆ACF)
Q.11. A rectangular metallic sheet has dimensions 48 cm × 36 cm. From each corner, a square of 8 cm is cut off. An open box is made of the remaining sheet. Find the volume of the box.
OR
Find the length of the diagonal in the following cases cuboid of 11 cm by 10 cm by 2 cm.
Ans. Length of the box = l = 48 – 8 – 8 = 32 cm
Breadth of the box = b = 36 – 8 – 8 = 20 cm
Height = h = 8 cm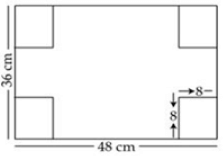 ► Volume of the box formed = l × b × h = 32 × 20 × 8 = 5120 cm3
► Volume of the box formed = l × b × h = 32 × 20 × 8 = 5120 cm3
OR
Given that:
Length (l) of cuboid = 11 cm
Breadth (b) of cuboid = 10 cm
Height (h) of cuboid = 2 cm
We know that,
Length of the diagonal in a Cuboid =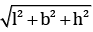
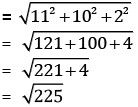
= 15 cm
Q.12. Find the value of k, if x = 1, y = 1 is a solution of the equation 9kx + 12ky = 63.
Ans. Since x = 1, y = 1 is the solution of 9kx + 12ky = 1, it will satisfy the equation.
► 9k(1) + 12k(1) = 63
► 9k + 12k = 63
► 21k = 63
► k = 3
Section C
Q.13. Simplify: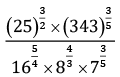
Ans.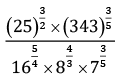
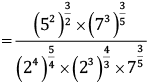
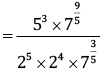

Q.14. (x + 2) is one of the factors of the polynomial x3 + 13x2 + 32x + 20. Find its remaining factors.
Ans. Let p(x) = x3 + 13x2 + 32x + 20
p(-1) = –1 + 13 – 32 + 20 = –33 + 33 = 0
Therefore (x + 1) is a factor of p(x).
On dividing p(x) by (x + 1), we get:
p(x) ÷ (x + 1) = x2 + 12x + 20
Thus,
x3 + 13x2 + 32x + 20 = (x + 1)(x2 + 12x + 20)
= (x + 1)(x2 + 10x + 2x + 20)
= (x + 1)[x(x + 10) + 2(x + 10)]
= (x + 1)(x +2)(x + 10)
Hence, x3 + 13x2 + 32x + 20 = (x + 1)(x +2)(x + 10)
Q.15. In the figure, it is given that LM = MN and LP = QN. Prove that ΔLMQ ≌ ΔNMP.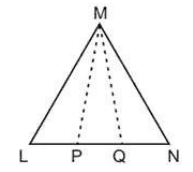 OR
OR
The following pairs of triangles are congruent? Give reasons.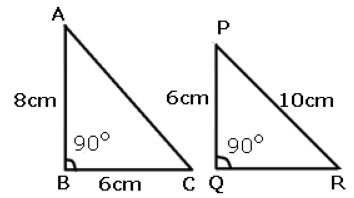 Ans. LM = MN (Given)
Ans. LM = MN (Given)
► ∠MLN = ∠MNL (angles opposite equal sides are equal)
► ∠MLQ = ∠MNP
LP = QN (Given)
► LP + PQ = PQ + QN (adding PQ on both sides)
► LQ = PN
In ΔLMQ and ΔNMP
LM = MN
∠MLQ = ∠MNP
LQ = PN
ΔLMQ ≌ ΔNMP (SAS congruence rule)
OR
In ΔABC and ΔPQR
∠B = ∠Q
BC = PQ
By Pythagoras theorem:
► PR2 = PQ2 + QR2
► 102 = 62 + QR2
► 100 = 36 + QR2
► QR =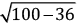
► QR = √64 = 8cm
► AB = QR
Therefore,
ΔABC ≌ ΔPQR (SAS and RHS criteria)
Q.16. The polynomials p(x) = ax3 + 3x2 – 3 and q(x) = 2x3 – 5x + a when divided by (x – 4) leave the remainders R1 and R2. Find ‘a’ if R1 + R2 = 0. Factorise the polynomial.
Ans. When p(x) = ax3 + 3x2 – 3 is divided by (x – 4 ), the remainder is given by:
R1 = a(4)3 + 3(4)2 – 3 = 64a + 45
When q(x) = 2x3 – 5x + a is divided by (x – 4), the remainder is given by:
R2 = 2(4)3 – 5(4) + a = 108 + a
Given: R1 + R2 = 0
► 65a + 153 = 0
► a = -153 / 65
By hit and trial we find x = 3 is factor of given polynomial, as:
2(3)3 – 9 – 39 – 6 = 54 – 54 = 0
By dividing 2x3 – x2 – 13x – 6 by (x – 3) we get 2x2 + 5x + 2 as quotient.
Now, 2x2 + 5x + 2 = 2x2 + 4x + x + 2 = 2x(x + 2) + 1(x + 2) = (2x + 1)(x + 2)
So, 2x3 – x2 – 13x – 6 = (2x + 1)(x + 2)(x – 3)
Q.17. In the figure, AB = AC, D is the point in the interior of ΔABC such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ΔABC.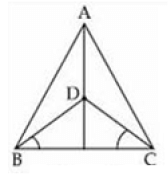 Ans. In ΔDCB, ∠DBC = ∠DCB (given)
Ans. In ΔDCB, ∠DBC = ∠DCB (given)
DC = DB [Side opp. To equal ∠'s are equal] ...(i)
In ΔABD and ΔACD
AB = AC (given)
BD = CD [from (i)]
AD = AD (common)
ΔABD ≌ ΔACD [SSS Rule]
∠BAD = ∠CAD (CPCT)
Hence, AD is the bisector of ∠BAC.
Q.18. A card is drawn at random from a well-shuffled deck of playing cards. Find the probability that the card drawn is a:
(a) queen
(b) non-ace card
(c) black card
Ans. Total number of outcomes = n(S) = 52
(a) Let A be the event when the card drawn is a queen.
Total number of queen cards = 4
► n(A) = 4
► P(A) = n(A) / n(S) = 4/52 = 1/13
(b) Let B be the event when the card drawn is a non-ace card.
Non–ace cards = 52 – 4 = 48
► n(B) = 48
► P(A) = n(B) / n(S) = 48/52 = 12/13
(c) Let C be the event when the card drawn is a black card.
Number of black cards = 26
► n(C) = 26
► P(A) = n(C) / n(S) = 26/52 = 1/2
Q.19. Show that the line segments joining the midpoints of the opposite sides of a quadrilateral bisect each other.
OR
Point M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.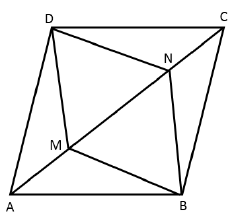 Ans. Let ABCD be a quadrilateral. P, Q, R, and S are the midpoints of AB, BC, CD and DA respectively.
Ans. Let ABCD be a quadrilateral. P, Q, R, and S are the midpoints of AB, BC, CD and DA respectively.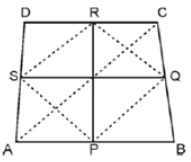 Join PQ, QR, RS and SP. Join AC.
Join PQ, QR, RS and SP. Join AC.
In ΔDAC, SR ‖ AC
And SR = 1/2 AC (Mid-point theorem)
In ΔBAC, PQ ∥ AC
And PQ = 1/2 AC
Clearly, PQ ∥ SR and PQ = SR
In quadrilateral PQRS, one pair of opposite sides is equal and parallel to each other and hence it is a parallelogram.
► Now, PR and SQ are the diagonals of PQRS and hence PR and SQ bisect each other.
OR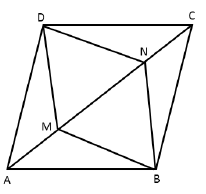 The diagonals of a parallelogram bisect each other.
The diagonals of a parallelogram bisect each other.
Therefore, AC and BD bisect each other.
► OA = OC
But AM = CN
Therefore, OA – AM = OC – CN
► OM = ON
Therefore, in quadrilateral BMDN,
OM = ON and OD = OB
► Diagonals MN and BD bisect each other
► BMDN is a parallelogram.
Q.20. In the given figure, ABCD is a cyclic quadrilateral, in which AC and BD are the diagonals. If m∠DBC = 55° and m∠BAC = 45°, find m∠BCD.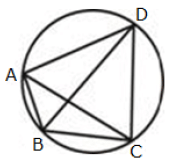 Ans. Given: ABCD is a cyclic quadrilateral in which AC and BD are diagonals.
Ans. Given: ABCD is a cyclic quadrilateral in which AC and BD are diagonals.
m∠DBC = 55° and m∠BAC = 45°
To find: m∠BCD
Proof: m∠CAD = m∠DBC = 55° (Angles in the same segment)
Therefore, m∠DAB = m∠CAD + m∠BAC
= 55° + 45°
= 100°
However, m∠DAB + m∠BCD = 180°
(∵ opposite angles of a cyclic quadrilateral)
So, m∠BCD = 180° – 100° = 80°
Q.21. The diameter of a roller is 84 cm and its length is 120 cm. It takes 500 complete revolutions to move over once to level a playground. Find the area of the playground in m2. (π = 22 / 7)
OR
A room is 22 m long, 15 m broad and 6 m high. Find the area of its four walls and the cost of painting it including doors and windows at the rate of Rs 12 per m2.
Ans. The roller is cylindrical in shape.
Height (h) of cylindrical roller = Length of roller = 120 cm
Radius (r) of the circular end of roller = (84 / 2)cm = 42 cm
C.S.A. of roller = 2πrh = 2 x 22 / 7 x 42 x 120 = 31680 cm2
Area of field = 500 × C.S.A. of roller = (500 × 31680) cm2 = 15840000 cm2
Area of field = 1584 m2
OR
Given that:
Length (l) of room = 22 m
Breadth (b) of room = 15 m &
Height (h) of room = 6 m
► L.S.A of room = 2 x h x (l + b)
= 2 x 6 x (22 + 15)
= 2 x 6 x 37
= 444 m2
► Area of its 4 walls = 444 m2
Cost of painting the walls = 12 per m2
i.e., for 1 m2 = Rs 12
► For 444 m2 = Rs 12 x 444
= Rs 5328
Q.22. The following observations have been arranged in ascending order.
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
If the median of the data is 63, find the value of x.
OR
The number of goals scored by Arsenal Football Club in the English Premier League in the season 2007 was:
1, 2, 1, 3, 2, 5, 1, 6, 4, 4, 2, 3, 5, 6, 4, 2, 2, 3, 4, 1, 0, 5, 0, 5, 3, 2, 3, 4, 4, 1, 1, 2, 4, 3, 1, 4
Arrange these data in a discrete frequency distribution table and answer the following:
(i) What is the range of the number of goals scored by AFC?
(ii) How many times did AFC score 3 or more than 3 goals?
(iii) Which variate has the highest frequency?
Ans. Total observations in the given data set, n = 10 (even)
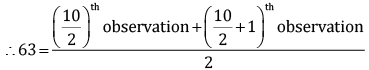
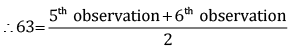
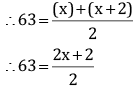
∴ 63 = x + 1
∴ x = 62
OR
The discrete frequency distribution table is as below: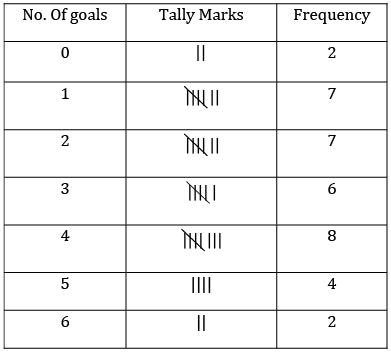
(i) Maximum goals scored = 6
Minimum goals scored = 0
∴ Range of the goals scored = 6 – 0 = 6
(ii) No. Of times AFC scored 3 or more goals = 6 + 8 + 4 + 2 = 20
(iii) The variate which has the highest frequency is 4.
Section D
Q.23. Find the value of: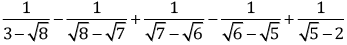
Ans. 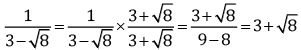
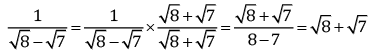
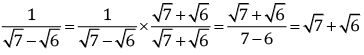
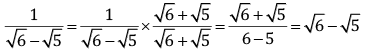
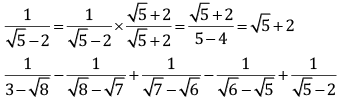
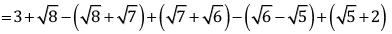
= 5
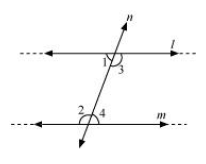
Q.24. How does Euclid's fifth postulate imply the existence of parallel lines? Give mathematical proof.
Ans.
- Euclid's 5th postulate states that: If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
- This implies that if n intersects lines l and m and if ∠1 + ∠2 < 180º, then ∠3 + ∠4 > 180º. In that case, producing line l and further will meet on the side of ∠1 and ∠2 which is less than 180º.
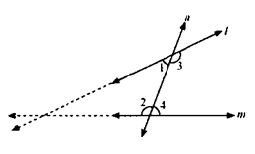
- If ∠1 + ∠2 = 180º, then ∠3 + ∠4 = 180º In that case, the lines l and m neither meet at the side of ∠1 and ∠2 nor at the side of ∠3 and ∠4 implying that the lines l and m will never intersect each other. Therefore, the lines are parallel.
Q.25. Simplify: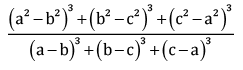
OR
Ans. Consider: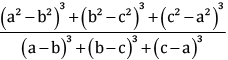
We know that:
If x + y + x = 0 then x3 + y3 + z3 = 3xyz
Now, a2 – b2 + b2 – c2 – a2 = 0
And, a – b +b – c + c – a = 0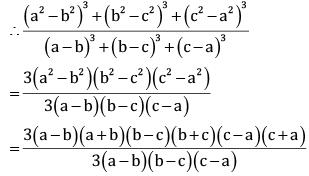
= (a + b)(b + c)(c +a)
OR
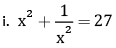
Squaring on both sides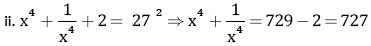
Q.26. In the figure, if AC = BC, ∠DCA = ∠ECB and ∠DBC = ∠EAC, then prove that BD = AE.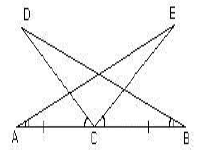 Ans. Given that ∠DCA = ∠ECB
Ans. Given that ∠DCA = ∠ECB
► ∠DCA + ∠ECD = ∠ECB + ∠ECD
► ∠ECA = ∠DCB ...(i)
Now in ΔDBC and ΔEAC
∠DCB = ∠ECA [from (i)]
BC = AC (Given)
∠DBC = ∠EAC (Given)
ΔDBC ≌ ΔEAC (ASA Congruence)
Therefore, BD = AE (CPCT)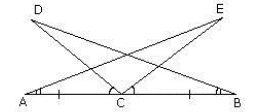
Q.27. The volume of a cylinder is 6358 cubic cm and its height is 28 cm. Find its radius and the curved surface area.
OR
Find the cost of sinking a tube well 350 m deep, having a diameter of 4 m at the rate of Rs 16 per m3. Find also the cost of cementing its inner curved surface at Rs 12 per m2.
Ans. Let the radius of the cylinder be ‘r’ cm.
► Volume of cylinder = πr2h = 22 / 7 x r2 x 28
► 6358 = 88r2
► r2 = 6358 / 88 = 289 / 4
► r = 17 / 2 cm = 8.5 cm
Curved surface area of cylinder 2πrh = 2 x 22 / 7 x 17 / 2 x 28 = 1496 cm2.
Thus, the radius of the cylinder is 8.5 cm and its curved surface area is 1796 cm2.
OR
Height (h) = 350 m Diameter = 4 m
► Radius (r) = 2 m
► Volume of tube well = π x r2 x h
= 22 / 7 x 22 x 350
= 440m3
► Cost of sinking the tube well = 4400 x Rs 16
= Rs 70400
► L.S.A. of cylindrical tube well = 2 x π x r x h
= 2 x 22 / 7 x 2 x 350
= 4400 m2
► Cost of cementing inner curved surface of the tube well = 4400 x Rs 12
= Rs 52800
Q.28. Construct a triangle having a perimeter of 12.5 cm and angles in the ratio of 3 : 4 : 5.
Ans. Steps of construction:
(i) Draw BC = 5 cm
(ii) Draw m∠CBX = 60° and cut off BD = 7.7 cm.
(iii) Join CD and draw its perpendicular bisector meeting BD at A.
(iv) Join AC. ΔABC is the required triangle.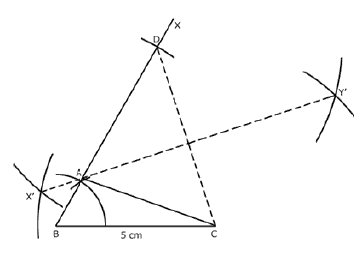
Q.29. If two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prove that the chords are equal.
OR
AC and BD are chords of a circle that bisect each other. Prove that:
(i) AC and BD are diameters
(ii) ABCD is a rectangle.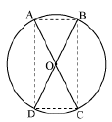 Ans. Given: AB and CD are two chords of a circle with centre O, intersecting at a point E.
Ans. Given: AB and CD are two chords of a circle with centre O, intersecting at a point E.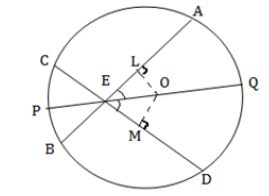 PQ is the diameter through E, such that ∠AEQ = ∠DEQ.
PQ is the diameter through E, such that ∠AEQ = ∠DEQ.
To Prove: AB = CD.
Proof: Draw perpendiculars OL and OM on chords AB and CD respectively.
Now, m∠LOE = 180° – 90° – m∠LEO ... [Angle sum property of a triangle]
= 90° – m∠LEO
► m∠LOE = 90° – m∠AEQ
► m∠LOE = 90° – m∠DEQ
► m∠LOE = 90° – m∠MEQ
► ∠LOE = ∠MOE
In ΔOLE and ΔOME, ∠LEO = ∠MEO
∠LOE = ∠MOE
EO = EO
ΔOLE ≅ ΔOME
OL = OM
Therefore, chords AB and CD are equidistant from the centre.
Hence, AB = CD
OR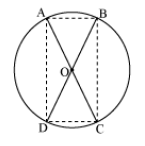
In ΔAOB and ΔCOD
OA = OC (given)
OB = OD (given)
∠AOB = ∠COD (vertically opposite angles)
ΔAOB ≌ ΔCOD (SAS congruence rule)
AB = CD (by CPCT)
Similarly, we can prove ΔAOD ≌ ΔCOB
∴ AD = CB (by CPCT) Since in quadrilateral ABCD opposite sides are equal in length.
Hence, ABCD is a parallelogram.
We know that opposite angles of a parallelogram are equal
4 ∠A = ∠C
But m∠A + m∠C = 180° (ABCD is a cyclic quadrilateral)
► m∠A + m∠A = 180°
► 2m ∠A = 180°
► m∠A = 90°
As ABCD is a parallelogram and one of its interior angles is 90°, so it is a rectangle.
∠A is the angle subtended by chord BD. And as m∠A = 90°, so BD should be the diameter of the circle. Similarly, AC is the diameter of the circle.
Q.30. Neha and Richa, two students of class IX of a school, together contributed Rs. 100 towards the Prime Minister’s Relief Fund, to help earthquake victims. Assume Neha’s contribution to be x and that of Richa to be y. Write a linear equation which this data satisfies and draw a graph of the same.
Ans. According to the given condition,
► x + y = 100 …(i)
Now, put the value x = 0 in equation (i).
► 0 + y = 100 ⇒ y = 100
The solution is (0, 100)
Putting the value x = 50 in equation (i), we get
► 50 + y = 100 ⇒ y = 100 – 50 ⇒ y = 50.
The solution is (50, 50).
Put the value x = 100 in equation (i).
► 100 + y = 100,
► y = 100 – 100 ⇒ y = 0.
The solution is (100, 0).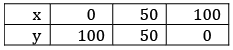
Now, plot the points (0, 100), (50, 50), (100, 0) and draw lines passing through the points.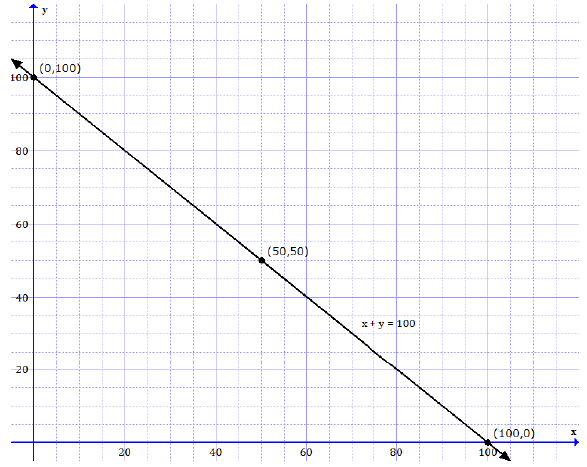
FAQs on Class 9 Math: Sample Question Paper- 1 (With Solutions)
| 1. What are the topics covered in Section A of the Class 9 Mathematics exam? |  |
| 2. How many marks are allotted to Section B in the Class 9 Mathematics exam? |  |
| 3. What topics are included in Section C of the Class 9 Mathematics exam? |  |
| 4. What is the time duration for the Class 9 Mathematics exam? |  |
| 5. How many marks are allocated to Section D in the Class 9 Mathematics exam? |  |














