NCERT Solutions for Class 8 Maths - Playing with Numbers - 1
Try These
Question 1: Write the following numbers in generalized form.
(i) 25 (ii) 73
(iii) 129 (iv) 302
Solution:
(i) 25 = 20 + 5
= 10 x 2 + 5 x 1 = 10 x 2 + 5
(ii) 73 = 70 + 3
= 10 x 7 + 3 x 1 = 10 x 7 + 3
(iii) 129 = 100 + 20 + 9
= 100 x 1 + 10 x 2 + 1 x 9 = 100 x 1 + 10 x 2 + 9
(iv) 302 = 300 + 2
= 100 x 3 + 10 x 0 + 1 x 2 = 300 + 0 + 2
Question 2: Write the following in the usual form.
(i) 10 x 5 + 6 (ii) 100 x 7 + 10 x 1 + 8
(iii) 100 x a + 10 x c + b
Solution:
(i) 10 x 5 + 6 = 50 + 6 = 56
(ii) 100 x 7 + 10 x 1 + 8 = 700 + 10 + 8 = 718
(iii) 100 x a + 10 x c + b = 100a + 10c + b =
Question 3: Check what the result would have been if sundaram had chosen the numbers shown below.
1) 27
Ans: Chosen number = 27
Nmber with reversed digits = 72
Sum of the two numbers = 27 + 72 = 99
Now, 99 = 11[9] = 11[2 + 7]
= 11[Sum of the digits of the chosen number]
2) 39
Ans: Chosen number = 39
Number with reversed digits = 93
Sum of the two numbers = 39 + 93 = 132
Now, 132 ÷ 11 = 12
i.e. 132 = 11[12] = 11[3 + 9]
= 11[Sum of the digits of the chosen number]
3) 64
Ans: Chosen number = 64
Number with reversed digits = 46
Sum = 64 + 46 = 110
Now, 110 = 11[10] = 11[6 + 4]
= 11[Sum of the digits of the chosen number]
4) 17
Ans: Chosen number = 17
Number with reversed digits = 71
Sum = 17 + 71 = 88
Now, 88 = 11[8] = 11[1+ 7]
= 11[Sum of the digits of the chosen number]
Question 4: Check what result would have been if Sundaram had chosen the numbers shown.
1) 17
Ans: Chosen number = 17
Number with reversed digits = 71
Difference = 71 – 17 = 54
= 9 x [6]
9 x [Difference of the digits of the chosen number (7 – 1 = 6)]
2) 21
Ans: Chosen number = 21
Number with reversed digits = 12
Difference = 21 – 12 = 9
= 9 x [1]
= 9 x [Difference between the digits of the chosen number (2 – 1 = 1)]
3) 96
Ans: Chosen number = 96
Number with reversed digits = 69
Difference = 96 – 69 = 27
= 9 x [3]
= 9 x [Difference between the digits of the chosen number (9 – 6 = 3)]
4) 37
Ans: Chosen number = 37
Number with reversed digits = 73
Difference = 73 – 37 = 36
= 9 x [4]
= 9 x [Difference between the digits of the chosen number (7 – 3 = 4)]
Question 5: Check what the result would have been if Minakshi had chosen the numbers shown below.
In each case keep a record of the quotient obtained at the end.
1) 132
Ans: Chosen number = 132
Reversed number = 231
Difference = 231 – 132 = 99
We have, 99 ÷ 99 = 1, remainder = 0
2) 469
Ans: Chosen number = 469
Reversed number = 964
Difference = 964 – 469 = 495
We have, 495 ÷ 99 = 5, remainder = 0
3) 737
Ans: Chosen number = 737
Reversed number = 737
We have Difference = 737 – 737 = 0
We have, 0 ÷ 99 = 0, remainder = 0
4) 901
Ans: Chosen number = 901
Reversed number = 109
Difference = 901 – 109 = 792
We have, 792 ÷ 99 = 8, remainder = 0
Forming three-digit number with given three digits
Note: Generalised form ofGeneralised form of
Generalised form of
Adding
which is divisible by 37
Question 6: Check what the result would have been if Sudaram had chosen the numbers shown below.
1) 417
Ans: Chosen number = 417
Two other numbers with the same digits are 741 and 174
Sum of the three numbers:-
We have 1332 ÷ 37 = 36, remainder = 0
2) 632
Ans: Chosen number = 632
Two other numbers are 263 and 326
Sum of the three numbers:-
We have 1221 ÷ 37 = 33, remainder = 0
3) 117
Ans: Chosen number = 117
Other numbers are 711 and 171
Sum of the three numbers:-
We have 999 ÷ 37 = 27, remainder = 0
4) 937
Ans: Chosen number = 937
Other two numbers are 793 and 379
Sum of the three numbers:-
We have 2109 ÷ 37 = 57, remainder = 0
Exercise 16.1
Find the values of the letters in each of the following and give reasons for the steps involved.
Question 1: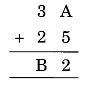
Solution: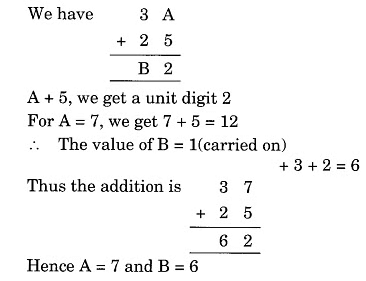
Question 2: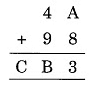
Solution: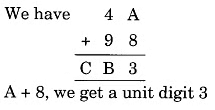
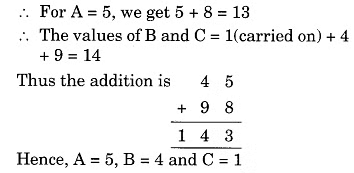
Question 3: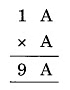
Solution: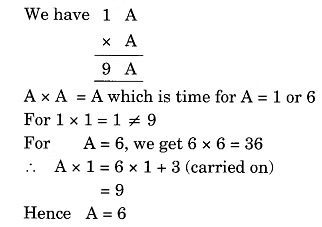
Question 4:
Solution:
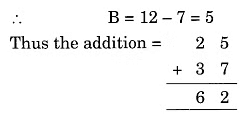
Question 5:
Solution:
3 × B = B
⇒ B = D
3 × A = CA
⇒ 3 × 5 = 15
Thus A = 5 and C = 1
Hence A = 5, B = 0 and C = 1
Question 6: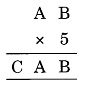
Solution:
5 × B = B
⇒ B = 0 or 5
5 × A = CA
5 × 5 = 25
Only possible when B = 0
Thus A = 5 and C = 2
Hence A = 5, B = 0 and C = 2
Question 7: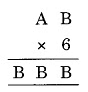
Solution:
B × 6 = B
6 × 4 = 24 → B = 4 and 2 is carried to
6 × A = BB
⇒ 6 × 7 = 42 + 2 (carried on) = 44
Thus B = 7
Hence A = 7 and B = 4
Question 8: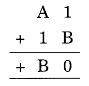
Solution:
1 + B = 0
1 + 9 = 10 → unit digit is 0 and 1 is carried to A
+ 1 +1 (carried on) = B = 9
A + 2 = 9 ⇒ A = 9 – 2 = 7
Hence A = 7 and B = 9
Question 9:
Solution:
B + 1 = 8 ⇒ B = 8 – 1 = 7
A + B = a number with unit digit 1
A + B = 11
⇒ A + 7 = 11
⇒ A = 11 – 7 = 4 (1 Carried to)
Now 1 carried on + 2 + A = B
3 + A = 7
⇒ A = 7 – 3 = 4
Hence A = 4, B = 7
Question 10:
Solution:
9 = A + B
9 = 1 + 8 or 2 + 7 or 3 + 6 or 4 + 5 or 8 + 1 or 7 + 2 or 6 + 3 or 5 + 4 or 0 + 9 or 9 + 0
Now 0 is required at unit place
2 + A = 10
⇒ A = 10 – 2 = 8
B = 9 – 8 = 1
1 + 6 + 1 (carried on) = A = 8
Hence A = 8 and B = 1
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Playing with Numbers - 1
| 1. How can I solve problems related to playing with numbers? |  |
| 2. What are some common mistakes to avoid while solving playing with numbers problems? |  |
| 3. Can you explain the concept of prime numbers in playing with numbers? |  |
| 4. How can I improve my problem-solving skills in playing with numbers? |  |
| 5. Are there any online resources available to help me with playing with numbers problems? |  |






















