NCERT Solutions Class 11 Maths Chapter 1 - Sets
EXERCISE - 1.4
Q1: Find the union of each of the following pairs of sets:
(i) X = {1, 3, 5} Y = {1, 2, 3}
(ii) A = {a, e, i, o, u} B = {a, b, c}
(iii) A = {x : x is a natural number and multiple of 3}
B = {x : x is a natural number less than 6}
(iv) A = {x : x is a natural number and 1 < x ≤ 6}
B = {x : x is a natural number and 6 < x < 10}
(v) A = {1, 2, 3}, B = Φ
Ans:
(i) X = {1, 3, 5} Y = {1, 2, 3}
X∪ Y= {1, 2, 3, 5}
(ii) A = {a, e, i, o, u} B = {a, b, c}
A∪ B = {a, b, c, e, i, o, u}
(iii) A = {x : x is a natural number and multiple of 3} = {3, 6, 9 …}
As B = {x : x is a natural number less than 6} = {1, 2, 3, 4, 5, 6}
A ∪ B = {1, 2, 4, 5, 3, 6, 9, 12 …}
∴ A ∪ B = {x : x = 1, 2, 4, 5 or a multiple of 3}
(iv) A = {x : x is a natural number and 1 < x ≤ 6} = {2, 3, 4, 5, 6}
B = {x : x is a natural number and 6 < x < 10} = {7, 8, 9}
A∪ B = {2, 3, 4, 5, 6, 7, 8, 9}
∴ A∪ B = {x : x ∈ N and 1 < x < 10}
(v) A = {1, 2, 3}, B = Φ
A∪ B = {1, 2, 3}
Q2: Let A = {a, b}, B = {a, b, c}. Is A ⊂ B? What is A ∪ B?
Ans: Here, A = {a, b} and B = {a, b, c}
Yes, A ⊂ B.
A∪ B = {a, b, c} = B
Q3: If A and B are two sets such that A ⊂ B, then what is A ∪ B?
Ans: If A and B are two sets such that A ⊂ B, then A ∪ B = B.
Q4: If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8} and D = {7, 8, 9, 10}; find
(i) A ∪ B
(ii) A ∪ C
(iii) B ∪ C
(iv) B ∪ D
(v) A ∪ B ∪ C
(vi) A ∪ B ∪ D
(vii) B ∪ C ∪ D
Ans: A = {1, 2, 3, 4], B = {3, 4, 5, 6}, C = {5, 6, 7, 8} and D = {7, 8, 9, 10}
(i) A ∪ B = {1, 2, 3, 4, 5, 6}
(ii) A ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
(iii) B ∪ C = {3, 4, 5, 6, 7, 8}
(iv) B ∪ D = {3, 4, 5, 6, 7, 8, 9, 10}
(v) A ∪ B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
(vi) A ∪ B ∪ D = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(vii) B ∪ C ∪ D = {3, 4, 5, 6, 7, 8, 9, 10}
Q5: Find the intersection of each pair of sets:
(i) X = {1, 3, 5} Y = {1, 2, 3}
(ii) A = {a, e, i, o, u} B = {a, b, c}
(iii) A = {x: x is a natural number and multiple of 3}
B = {x: x is a natural number less than 6}
(iv) A = {x : x is a natural number and 1 < x ≤ 6}
B = {x : x is a natural number and 6 < x < 10}
(v) A = {1, 2, 3}, B = Φ
Ans: (i) X = {1, 3, 5}, Y = {1, 2, 3}
X ∩ Y = {1, 3}
(ii) A = {a, e, i, o, u}, B = {a, b, c}
A ∩ B = {a}
(iii) A = {x : x is a natural number and multiple of 3} = (3, 6, 9 …}
B = {x : x is a natural number less than 6} = {1, 2, 3, 4, 5}
∴ A ∩ B = {3}
(iv) A = {x : x is a natural number and 1 < x ≤ 6} = {2, 3, 4, 5, 6}
B = {x : x is a natural number and 6 < x < 10} = {7, 8, 9}
A ∩ B = Φ
(v) A = {1, 2, 3}, B = Φ
A ∩ B = Φ
Q6: If A = {3, 5, 7, 9, 11}, B = {7, 9, 11, 13}, C = {11, 13, 15} and D = {15, 17}; find
(i) A ∩ B
(ii) B ∩ C
(iii) A ∩ C ∩ D
(iv) A ∩ C
(v) B ∩ D
(vi) A ∩ (B ∪ C)
(vii) A ∩ D
(viii) A ∩ (B ∪ D)
(ix) (A ∩ B) ∩ (B ∪ C)
(x) (A ∪ D) ∩ (B ∪ C)
Ans:
(i) A ∩ B = {7, 9, 11}
(ii) B ∩ C = {11, 13}
(iii) A ∩ C ∩ D = { A ∩ C} ∩ D = {11} ∩ {15, 17} = Φ
(iv) A ∩ C = {11}
(v) B ∩ D = Φ
(vi) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
= {7, 9, 11} ∪ {11} = {7, 9, 11}
(vii) A ∩ D = Φ
(viii) A ∩ (B ∪ D) = (A ∩ B) ∪ (A ∩ D)
= {7, 9, 11} ∪ Φ = {7, 9, 11}
(ix) (A ∩ B) ∩ (B ∪ C) = {7, 9, 11} ∩ {7, 9, 11, 13, 15} = {7, 9, 11}
(x) (A ∪ D) ∩ (B ∪ C) = {3, 5, 7, 9, 11, 15, 17) ∩ {7, 9, 11, 13, 15}
= {7, 9, 11, 15}
Q7: If A = {x : x is a natural number}, B ={x : x is an even natural number}
C = {x : x is an odd natural number} and D = {x : x is a prime number}, find
(i) A ∩ B
(ii) A ∩ C
(iii) A ∩ D
(iv) B ∩ C
(v) B ∩ D
(vi) C ∩ D
Ans: A = {x : x is a natural number} = {1, 2, 3, 4, 5 …}
B ={x : x is an even natural number} = {2, 4, 6, 8 …}
C = {x : x is an odd natural number} = {1, 3, 5, 7, 9 …}
D = {x : x is a prime number} = {2, 3, 5, 7 …}
(i) A ∩B = {x : x is a even natural number} = B
(ii) A ∩ C = {x : x is an odd natural number} = C
(iii) A ∩ D = {x : x is a prime number} = D
(iv) B ∩ C = Φ
(v) B ∩ D = {2}
(vi) C ∩ D = {x : x is odd prime number}
Q8: Which of the following pairs of sets are disjoint
(i) {1, 2, 3, 4} and {x : x is a natural number and 4 ≤ x ≤ 6}
(ii) {a, e, i, o, u} and {c, d, e, f}
(iii) {x : x is an even integer} and {x : x is an odd integer}
Ans: (i) {1, 2, 3, 4}
{x : x is a natural number and 4 ≤ x ≤ 6} = {4, 5, 6}
Now, {1, 2, 3, 4} ∩ {4, 5, 6} = {4}
Therefore, this pair of sets is not disjoint.
(ii) {a, e, i, o, u} ∩ (c, d, e, f} = {e}
Therefore, {a, e, i, o, u} and (c, d, e, f} are not disjoint.
(iii) {x : x is an even integer} ∩ {x : x is an odd integer} = Φ
Therefore, this pair of sets is disjoint.
Q9: If A = {3, 6, 9, 12, 15, 18, 21},
B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16},
D = {5, 10, 15, 20}; find
(i) A – B
(ii) A – C
(iii) A – D
(iv) B – A
(v) C – A
(vi) D – A
(vii) B – C
(viii) B – D
(ix) C – B
(x) D – B
(xi) C – D
(xii) D – C
Ans:
(i) A – B = {3, 6, 9, 15, 18, 21}
(ii) A – C = {3, 9, 15, 18, 21}
(iii) A – D = {3, 6, 9, 12, 18, 21}
(iv) B – A = {4, 8, 16, 20}
(v) C – A = {2, 4, 8, 10, 14, 16}
(vi) D – A = {5, 10, 20}
(vii) B – C = {20}
(viii) B – D = {4, 8, 12, 16}
(ix) C – B = {2, 6, 10, 14}
(x) D – B = {5, 10, 15}
(xi) C – D = {2, 4, 6, 8, 12, 14, 16}
(xii) D – C = {5, 15, 20}
Q10: If X = {a, b, c, d} and Y = {f, b, d, g}, find
(i) X – Y
(ii) Y – X
(iii) X ∩ Y
Ans:
(i) X – Y = {a, c}
(ii) Y – X = {f, g}
(iii) X ∩ Y = {b, d}
Q11: If R is the set of real numbers and Q is the set of rational numbers, then what is R – Q?
Ans: R: set of real numbers
Q: set of rational numbers
Therefore, R – Q is a set of irrational numbers.
Q12: State whether each of the following statement is true or false. Justify your answer.
(i) {2, 3, 4, 5} and {3, 6} are disjoint sets.
(ii) {a, e, i, o, u } and {a, b, c, d} are disjoint sets.
(iii) {2, 6, 10, 14} and {3, 7, 11, 15} are disjoint sets.
(iv) {2, 6, 10} and {3, 7, 11} are disjoint sets.
Ans: (i) False
As 3 ∈ {2, 3, 4, 5}, 3 ∈ {3, 6}
⇒ {2, 3, 4, 5} ∩ {3, 6} = {3}
(ii) False
As a ∈ {a, e, i, o, u}, a ∈ {a, b, c, d}
⇒ {a, e, i, o, u } ∩ {a, b, c, d} = {a}
(iii) True
As {2, 6, 10, 14} ∩ {3, 7, 11, 15} = Φ
(iv) True
As {2, 6, 10} ∩ {3, 7, 11} = Φ
EXERCISE - 1.5
Q1: Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4}, B = {2, 4, 6, 8} and C = {3, 4, 5, 6}. Find
(i) A'
(ii) B'
(iii) (A ∪ C)'
(iv) (A ∪ B)'
(v) (A')'
(vi) (B - C)'
Ans:
U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {1, 2, 3, 4}
B = {2, 4, 6, 8}
C = {3, 4, 5, 6}
(i) A' = {5, 6, 7, 8 ,9}
(ii) B' = {1, 3, 5, 7, 9}
(iii) A ∪ C = {1, 2, 3, 4, 5, 6} ∴ (A ∪ C)' = {7, 8, 9}
(iv) A ∪ B = {1, 2, 3, 4, 6, 8} (A ∪ B)' = {5, 7, 9}
(v) (A')' = A = {1, 2, 3, 4}
(vi) B - C = {2, 8} ∴ (B - C)' = {1, 3, 4, 5, 6, 7, 9}
Q2: If U = {a, b, c, d, e, f, g, h}, find the complements of the following sets
(i) A = {a, b, c}
(ii) B = {d, e, f, g}
(iii) C = {a, c, e, g}
(iv) D = {f, g, h, a}
Ans: U = {a, b, c, d, e, f, g, h}
(i) A = {a, b, c} A' = {d, e, f, g, h}
(ii) B = {d, e, f, g} ∴ B' = {a, b, c, h}
(iii) C = {a, c, e, g} ∴ C' = {b, d, f, h}
(iv) D = {f, g, h, a} ∴ D' = {b, c, d, e}
Q3: Taking the set of natural numbers as the universal set, write down the complements of the following sets:
(i) {x : x is an even natural number}
(ii) {x : x is an odd natural number}
(iii) {x : x is a positive multiple of 3}
(iv) {x : x is a prime number}
(v) {x : x is a natural number divisible by 3 and 5}
(vi) {x : x is a perfect square}
(vii) {x : x is perfect cube}
(viii) {x : x + 5 = 8}
(ix) {x : 2x + 5 = 9}
(x) {x : x ≥ 7}
(xi) {x : x ∈ N and 2x + 1 > 10}
Ans: U = N: Set of natural numbers
(i) {x : x is an even natural number}´ = {x : x is an odd natural number}
(ii) {x : x is an odd natural number}´ = {x : x is an even natural number}
(iii) {x : x is a positive multiple of 3}´ = {x : x ∈ N and x is not a multiple of 3}
(iv) {x : x is a prime number}´ = {x : x is a positive composite number and x = 1}
(v) {x : x is a natural number divisible by 3 and 5}´ = {x : x is a natural number that is not divisible by 3 or 5}
(vi) {x : x is a perfect square}´ = {x : x ∈ N and x is not a perfect square}
(vii) {x : x is a perfect cube}´ = {x : x ∈ N and x is not a perfect cube}
(viii) {x : x + 5 = 8}´ = {x : x ∈ N and x ≠ 3}
(ix) {x : 2x + 5 = 9}´ = {x : x ∈ N and x ≠ 2}
(x) {x : x ≥ 7}´ = {x : x ∈ N and x < 7}
(xi) {x : x ∈ N and 2x + 1 > 10}´ = {x : x ∈ N and x ≤ 9/2}
Q4: If U = {1, 2, 3, 4, 5,6,7,8, 9}, A = {2, 4, 6, 8} and B = {2, 3, 5, 7}. Verify that
(i) (A U B)' = A' ∩ B'
(ii) (A ∩ B)' = A' U B'
Ans: It is given that
U = {1, 2, 3, 4, 5,6,7,8, 9}
A = {2, 4, 6, 8}
B = {2, 3, 5, 7}
(i) (A U B)' = {2, 3, 4, 5, 6, 7, 8}' = {1, 9}
A' ∩ B' = {1, 3, 5, 7, 9} ∩ {1, 4, 6, 8, 9} = {1, 9}
Therefore, (A U B)' = A' ∩ B'.
(ii) (A ∩ B)' = {2}' = {1, 3, 4, 5, 6, 7, 8, 9}
A' U B' = {1, 3, 5, 7, 9} U {1, 4, 6, 8, 9} = {1, 3, 4, 5, 6, 7, 8, 9}
Therefore, (A ∩ B)' = A' U B'.
Q5: Draw appropriate Venn diagrams for each of the following:
(i) (A ∪ B)'
(ii) A' ∩ B'
(iii) (A ∩ B)'
(iv) A' ∪ B'
Ans:
(i) In the diagrams, shaded portion represents (A ∪ B)'

(ii) In the diagrams, shaded portion represents A' ∩ B'
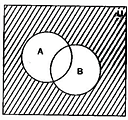
(iii) In the diagrams, shaded portion represents (A ∩ B)'
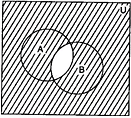
(iv) In the diagrams, shaded portion represents A' ∪ B'

Q6: Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60º what is A’?
Ans: Given: U = {x : x is a triangle}
A = {x : x is a triangle and has at least one angle different from 60º}
∴ A' = U – A = {x : x is a triangle and has all angles equal to 60º}
= Set of all equilateral triangles
Q7: Fill in the blanks to make each of the following a true statement:
(i) A'∪A' = ____
(ii) ϕ'∩A = ____
(iii) A'∩A' = ____
(iv) U'∩A' = ____
Ans:
(i) A'∪ A' = U
(ii) ϕ'∩ A = U ∩ A = A
(iii) A'∩ A' = ϕ
(iv) U'∩ A' = ϕ∩ A = ϕ
Old NCERT Questions
EXERCISE - 1.5
Q1: If X and Y are two sets such that n(X) = 17, n(Y) = 23 and n(X ∪ Y) = 38, find n(X ∩ Y).
Ans: Given
n (X) = 17
n (Y) = 23
n (X U Y) = 38
We can write it as
n (X U Y) = n (X) + n (Y) – n (X ∩ Y)
Substituting the values
38 = 17 + 23 – n (X ∩ Y)
By further calculation
n (X ∩ Y) = 40 – 38 = 2
So we get
n (X ∩ Y) = 2
Q2: If X and Y are two sets such that X ∪Y has 18 elements, X has 8 elements and Y has 15 elements; how many elements does X ∩ Y have?
Ans: Given
n (X U Y) = 18
n (X) = 8
n (Y) = 15
We can write it as
n (X U Y) = n (X) + n (Y) – n (X ∩ Y)
Substituting the values
18 = 8 + 15 – n (X ∩ Y)
By further calculation
n (X ∩ Y) = 23 – 18 = 5
So we get
n (X ∩ Y) = 5
Q3: In a group of 400 people, 250 can speak Hindi and 200 can speak English. How many people can speak both Hindi and English?
Ans: Consider H as the set of people who speak Hindi
E as the set of people who speak English
We know that
n(H ∪ E) = 400
n(H) = 250
n(E) = 200
It can be written as
n(H ∪ E) = n(H) + n(E) – n(H ∩ E)
By substituting the values
400 = 250 + 200 – n(H ∩ E)
By further calculation
400 = 450 – n(H ∩ E)
So we get
n(H ∩ E) = 450 – 400
n(H ∩ E) = 50
Therefore, 50 people can speak both Hindi and English.
Q4: If S and T are two sets such that S has 21 elements, T has 32 elements, and S ∩ T has 11 elements, how many elements does S ∪ T have?
Ans: We know that
n(S) = 21
n(T) = 32
n(S ∩ T) = 11
It can be written as
n (S ∪ T) = n (S) + n (T) – n (S ∩ T)
Substituting the values
n (S ∪ T) = 21 + 32 – 11
So we get
n (S ∪ T)= 42
Therefore, the set (S ∪ T) has 42 elements.
Q5: If X and Y are two sets such that X has 40 elements, X ∪Y has 60 elements and X ∩Y has 10 elements, how many elements does Y have?
Ans: We know that
n(X) = 40
n(X ∪ Y) = 60
n(X ∩ Y) = 10
It can be written as
n(X ∪ Y) = n(X) + n(Y) – n(X ∩ Y)
By substituting the values
60 = 40 + n(Y) – 10
On further calculation
n(Y) = 60 – (40 – 10) = 30
Therefore, the set Y has 30 elements.
Q6: In a group of 70 people, 37 like coffee, 52 like tea, and each person likes at least one of the two drinks. How many people like both coffee and tea?
Ans: Consider C as the set of people who like coffee
T as the set of people who like tea
n(C ∪ T) = 70
n(C) = 37
n(T) = 52
It is given that
n(C ∪ T) = n(C) + n(T) – n(C ∩ T)
Substituting the values
70 = 37 + 52 – n(C ∩ T)
By further calculation
70 = 89 – n(C ∩ T)
So we get
n(C ∩ T) = 89 – 70 = 19
Therefore, 19 people like both coffee and tea.
Q7: In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis?
Ans: Consider C as the set of people who like cricket
T as the set of people who like tennis
n(C ∪ T) = 65
n(C) = 40
n(C ∩ T) = 10
It can be written as
n(C ∪ T) = n(C) + n(T) – n(C ∩ T)
Substituting the values
65 = 40 + n(T) – 10
By further calculation
65 = 30 + n(T)
So we get
n(T) = 65 – 30 = 35
Hence, 35 people like tennis.
We know that,
(T – C) ∪ (T ∩ C) = T
So we get,
(T – C) ∩ (T ∩ C) = Φ
Here
n (T) = n (T – C) + n (T ∩ C)
Substituting the values
35 = n (T – C) + 10
By further calculation
n (T – C) = 35 – 10 = 25
Therefore, 25 people like only tennis.
Q8: In a committee, 50 people speak French, 20 speak Spanish and 10 speak both Spanish and French. How many speak at least one of these two languages?
Ans: Consider F as the set of people in the committee who speak French
S as the set of people in the committee who speak Spanish
n(F) = 50
n(S) = 20
n(S ∩ F) = 10
It can be written as
n(S ∪ F) = n(S) + n(F) – n(S ∩ F)
By substituting the values
n(S ∪ F) = 20 + 50 – 10
By further calculation
n(S ∪ F) = 70 – 10
n(S ∪ F) = 60
Therefore, 60 people in the committee speak at least one of the two languages
Exercise - 1.6
Q1: If X and Y are two sets such that n(X) = 17, n(Y) = 23 and n(X ∪ Y) = 38, find n(X ∩ Y).
Ans: Given
n (X) = 17
n (Y) = 23
n (X U Y) = 38
We can write it as
n (X U Y) = n (X) + n (Y) – n (X ∩ Y)
Substituting the values
38 = 17 + 23 – n (X ∩ Y)
By further calculation
n (X ∩ Y) = 40 – 38 = 2
So we get
n (X ∩ Y) = 2
Q2: If X and Y are two sets such that X ∪Y has 18 elements, X has 8 elements and Y has 15 elements; how many elements does X ∩ Y have?
Ans: Given
n (X U Y) = 18
n (X) = 8
n (Y) = 15
We can write it as
n (X U Y) = n (X) + n (Y) – n (X ∩ Y)
Substituting the values
18 = 8 + 15 – n (X ∩ Y)
By further calculation
n (X ∩ Y) = 23 – 18 = 5
So we get
n (X ∩ Y) = 5
Q3: In a group of 400 people, 250 can speak Hindi and 200 can speak English. How many people can speak both Hindi and English?
Ans: Consider H as the set of people who speak Hindi
E as the set of people who speak English
We know that
n(H ∪ E) = 400
n(H) = 250
n(E) = 200
It can be written as
n(H ∪ E) = n(H) + n(E) – n(H ∩ E)
By substituting the values
400 = 250 + 200 – n(H ∩ E)
By further calculation
400 = 450 – n(H ∩ E)
So we get
n(H ∩ E) = 450 – 400
n(H ∩ E) = 50
Therefore, 50 people can speak both Hindi and English.
Q4: If S and T are two sets such that S has 21 elements, T has 32 elements, and S ∩ T has 11 elements, how many elements does S ∪ T have?
Ans: We know that
n(S) = 21
n(T) = 32
n(S ∩ T) = 11
It can be written as
n (S ∪ T) = n (S) + n (T) – n (S ∩ T)
Substituting the values
n (S ∪ T) = 21 + 32 – 11
So we get
n (S ∪ T)= 42
Therefore, the set (S ∪ T) has 42 elements.
Q5: If X and Y are two sets such that X has 40 elements, X ∪Y has 60 elements and X ∩Y has 10 elements, how many elements does Y have?
Ans: We know that
n(X) = 40
n(X ∪ Y) = 60
n(X ∩ Y) = 10
It can be written as
n(X ∪ Y) = n(X) + n(Y) – n(X ∩ Y)
By substituting the values
60 = 40 + n(Y) – 10
On further calculation
n(Y) = 60 – (40 – 10) = 30
Therefore, the set Y has 30 elements.
Q6: In a group of 70 people, 37 like coffee, 52 like tea, and each person likes at least one of the two drinks. How many people like both coffee and tea?
Ans: Consider C as the set of people who like coffee
T as the set of people who like tea
n(C ∪ T) = 70
n(C) = 37
n(T) = 52
It is given that
n(C ∪ T) = n(C) + n(T) – n(C ∩ T)
Substituting the values
70 = 37 + 52 – n(C ∩ T)
By further calculation
70 = 89 – n(C ∩ T)
So we get
n(C ∩ T) = 89 – 70 = 19
Therefore, 19 people like both coffee and tea.
Q7: In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis?
Ans: Consider C as the set of people who like cricket
T as the set of people who like tennis
n(C ∪ T) = 65
n(C) = 40
n(C ∩ T) = 10
It can be written as
n(C ∪ T) = n(C) + n(T) – n(C ∩ T)
Substituting the values
65 = 40 + n(T) – 10
By further calculation
65 = 30 + n(T)
So we get
n(T) = 65 – 30 = 35
Hence, 35 people like tennis.
We know that,
(T – C) ∪ (T ∩ C) = T
So we get,
(T – C) ∩ (T ∩ C) = Φ
Here
n (T) = n (T – C) + n (T ∩ C)
Substituting the values
35 = n (T – C) + 10
By further calculation
n (T – C) = 35 – 10 = 25
Therefore, 25 people like only tennis.
Q8: In a committee, 50 people speak French, 20 speak Spanish and 10 speak both Spanish and French. How many speak at least one of these two languages?
Ans: Consider F as the set of people in the committee who speak French
S as the set of people in the committee who speak Spanish
n(F) = 50
n(S) = 20
n(S ∩ F) = 10
It can be written as
n(S ∪ F) = n(S) + n(F) – n(S ∩ F)
By substituting the values
n(S ∪ F) = 20 + 50 – 10
By further calculation
n(S ∪ F) = 70 – 10
n(S ∪ F) = 60
Therefore, 60 people in the committee speak at least one of the two languages.
|
75 videos|238 docs|91 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 1 - Sets
| 1. What are the basic operations that can be performed on sets? |  |
| 2. How are elements represented in a set? |  |
| 3. What is the cardinality of a set? |  |
| 4. How can we determine if two sets are equal? |  |
| 5. How can we represent a set using roster form? |  |

|
Explore Courses for Commerce exam
|

|


















