Class 10 Maths Chapter 4 Question Answers - Quadratic Equations
SHORT ANSWER TYPE QUESTIONS
Q1. Solve 2x2 − 5x + 3 = 0.
Sol. We have:
2x2 − 5x + 3 = 0 ...(1)
Comparing (1) with ax2 + bx + c = 0,
∴ a = 2
b = − 5
c = 3
∴ b2 − 4ac =(− 5)2 − 4 (2) (3)
25 − 24 = 1
Since, 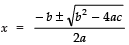
∴ 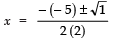
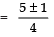
Taking, + ve sign,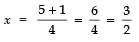
Taking, −ve sign,
Thus, the required roots are
x = 3/2 and x = 1
Q2. Solve the following quadratic equation:
x2 + 4x − 8 = 0
Sol. We have:
2x2 + 4x − 8= 0
Dividing by 2, we get
x2 + 2x − 4 = 0 ...(1)
Comparing (1) with ax2 + bx + c = 0,
a = 1
b = 2
c = − 4
∴ b2 − 4ac = (2)2 − 4 (1) (− 4)
= 4 + 16 = 20
Since, 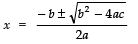
∴ 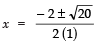
⇒ 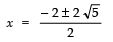
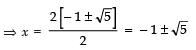
Taking +ve sign, we get
Taking −ve sign we get,
Thus, the required roots are x =
Sol. We have,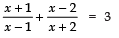
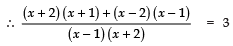
⇒ x2 + 3x + 2 + x2 − 3x + 2 =3 (x2 + x − 2)
⇒ 2x2 + 4 = 3x2 + 3x − 6
⇒ 3x2 + 3x − 6 − 2x2 − 4=0
⇒ x2 + 3x − 10 = 0
⇒ x2 + 5x − 2x − 10 = 0
⇒ x (x + 5) − 2 (x + 5) = 0
⇒ (x + 5) (x − 2) = 0
Either x + 5 = 0 ⇒ x = − 5
or x − 2 = 0 ⇒ x = 2
Thus, the required roots are
x = − 5 and x = 2
Q4. Solve (using quadratic formula):
x2 + 5x + 5 = 0
Sol. We have: x2 + 5x + 5 = 0
Comparing (1) with ax2 + bx + c = 0, we have:
a = 1
b = 5
c = 5
∴ b2 − 4ac = (5)2 − 4 (1) (5)
= 25 − 20 = 5
Since, 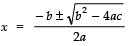
∴ 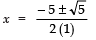
⇒ 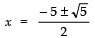
Taking +ve sign, we have:
Taking −ve sign, we have:
Thus, the required roots are:
Q5. Solve for x: 36x2 − 12ax + (a2 − b2) = 0.
Sol. We have:
36x2 − 12ax + (a2 − b2) = 0 ...(1)
Comparing (1) with Ax2 + Bx + C = 0, we have:
A = 36
B = − 12a
C = (a2 − b2)
∴ B2 − 4AC =[− 12a]2 − 4 (36) [a2 − b2]
= 144 a2 − 144 (a2 − b2)
= 144 a2 − 144 a2 + 144 b2
= 144 b2
Taking +ve sign, we have: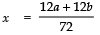
⇒ 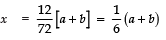
Taking −ve sign, we get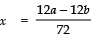
⇒ 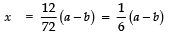
Thus, the required roots are:
Q6. Find the roots of the quadratic equation using the quadratic formula.
Sol. Comparing the given equation with the general equation ax2 + bx + c = 0, we have
= 5 + 16
= 21
Now, using the quadratic formula, we have: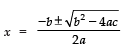
⇒ 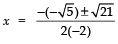
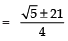
Taking the, positive sign, we get
Taking the negative sign, we get
Q7. Solve: 16x2 − 8a2 x + (a4 − b4) = 0 for x.
Sol. We have:
16x2 − 8a2 x + a4 − b4 = 0 ...(1)
Comparing (1) with ax2 + bx + c = 0, we get
a = 16
b = − 8a2
c =(a4 − b4)
∴ b2 − 4ac =[− 8a2]2 − 4 (16) (a4 − b4)
= 64 a4 − 64 (a4 − b4)
= 64 a4 − 64 a4 + 64 b4
= 64 b4
Since, 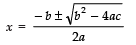
∴ 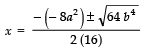
⇒ 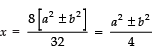
Now, taking +ve sign, we get
Taking −ve sign, we get
Thus, the required roots are:
Q8. Solve for x: 9x2 − 6ax + a2 − b2 = 0.
Sol. We have:
9x2 − 6ax + (a2 − b2) = 0 ...(1)
Comparing (1) with ax2 + bx + c = 0, we get
a = 9, b = − 6a and c = (a2 − b2)
∴ b2 − 4ac = (− 6a)2 − 4 (9) (a2 − b2)
= 36a2 − 36 (a2 − b2)
= 36a2 − 36a2 + 36b2
= 36b2 = (6b)2
Since, 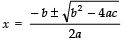
∴ 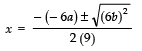
⇒ 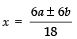
⇒ 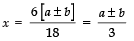
Taking the +ve sign, we get
Taking the −ve sign, we get
∴ The required roots are:
Q9. Evaluate 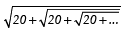
Sol. 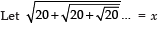
The given expression can be written as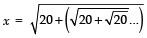
or 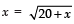
squaring both side, we have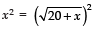
⇒ x2 = 20 + x
⇒ x2 – x – 20 = 0, where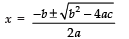
Here : a =1, b = –1 and c = –20
∴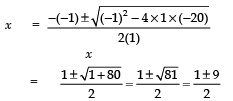
Since the given expression is positive,
∴ Rejecting the negative sign, we have:
Q10. Using quadratic formula, solve the following quadratic equation for x:
x2 − 4ax + 4a2 − b2 = 0
Sol. Comparing the given equation with ax2 + bx + c = 0, we have:
a = 1
b = − 4a
c = 4a2 − b2
∴ b2 − 4ac =[− (4a)]2 − 4 (1) [4a2 − b2]
= 16a2 − 4 (4a2 − b2)
= 16a2 − 16a2 + 4b2
= 4b2
= (2b)2
Since, 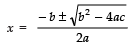
∴ 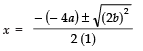
⇒ 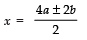
⇒ 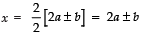
Taking the +ve sign, x = 2a + b
Taking the −ve sign, x = 2a − b
Thus, the required roots are:
x = 2a + b and x = 2a − b
Q11. Using quadratic formula, solve the following quadratic equation for x:
x2 − 2ax + (a2 − b2) = 0
Sol. Comparing the given equation with ax2 + bx + c = 0, we have:
a = 1, b = − 2a and c = (a2 − b2)
∴ b2 − 4ac =(− 2a)2 − 4 (1) (a2 − b2)
= 4a2 − 4 (a2 − b2)
= 4a2 − 4a2 + 4b2 = 4b2
Taking the +ve sign, we get
x = a + b
Taking the −ve sign, we get
x = a − b
Thus, the required roots are:
x = a + b and x = a − b
Q12. Solve for x :
Sol. We have: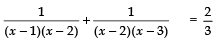
⇒ 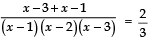
⇒ 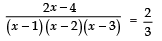
⇒ 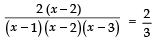
⇒ 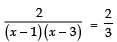
⇒ 2 × 3 = 2 (x − 1) (x − 3)
⇒ 3 = (x − 1) (x − 3)
⇒ x2 − 4x + 3 − 3 = 0
⇒ x2 − 4x = 0
⇒ x(x − 4) = 0
Either x = 0 or x = 4
Thus, x = 0 ; 4
Q13. Find the roots of the equation: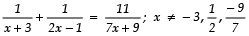
Sol. We have: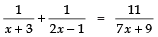
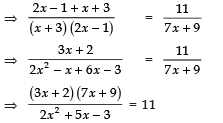
⇒ (3x + 2) (7x + 9) = 11 (2x2 + 5x − 3)
⇒ 21x2 + 27x + 14x + 18 = 22x2 + 55x − 33
⇒ 21x2 + 41x + 18 = 22x2 + 55x − 33
⇒ (21 − 22) x2 + (41 − 55)x + (18 + 33) = 0
⇒ − x2 + (− 14x) + (51) = 0
⇒ x2 + 14x − 51 = 0
⇒ x2 + 17x − 3x − 51 = 0
⇒ x (x + 17) − 3 (x + 17) = 0
⇒ (x + 17) (x − 3) = 0
Either x + 17 =0 ⇒ x = − 17
or x − 3 = 0 ⇒ x = 3
Thus, the required roots of the given equation are:
3 and −17
Q14. Find the roots of the equation:
Sol. We have:
⇒ 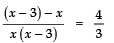
⇒ − 3 × 3 = 4 × (x2 − 3x)
⇒ − 9 = 4x2 − 12x
⇒ 4x2 − 12x + 9 = 0 ...(1)
Comparing (1), with ax2 + bx + c = 0, we get
a = 4
b = − 12
c = 9
∴ b2 − 4ac =(− 12)2 − 4 (4) (9)
= 144 − 144 = 0
Now, the roots are: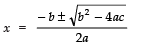
⇒ 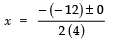
⇒ x = 12/8 = 3/2
Thus, the roots are: 3/2 and 3/2
Q15. Solve for x :
Sol.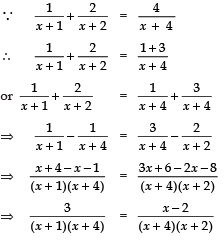
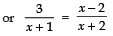
⇒ 3 (x + 2) =(x − 2) (x + 1) or 3x + 6
= x2 − x − 2
⇒ x2 − 4x − 8 = 0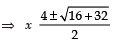
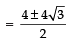
Q16. Find the roots of the equation:
Sol. We have: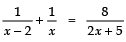
⇒ 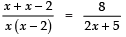
⇒ 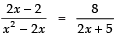
⇒ (2x − 2) (2x + 5) = 8 (x2 − 2x)
⇒ 4x2 + 10x − 4x − 10 = 8x2 − 16x
⇒− 4x2 + 22x − 10 = 0
⇒ 2x2 − 11x + 5 = 0 ...(1)
Comparing (1) with ax2 + bx + c = 0, we have:
a = 2
b = − 11
c = 5
∴ b2 − 4ac = (− 11)2 − 4 (2) (5)
= 121 − 40 = 81
Now, the roots are given by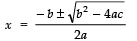
⇒ 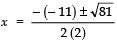
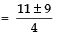
Taking the +ve sign,
Taking the −ve sign,
Thus, the required roots are: 5 and 1/2.
Q17. Solve :
Sol. We have: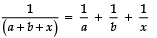
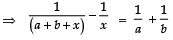
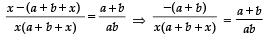
⇒ x (a + b + x) = −ab
⇒ x2 + (a + b)x + ab = 0
⇒ x2 + ax + bx + ab = 0
⇒ x (x + a) + b (x + a) = 0
⇒ (x + a) (x + b) = 0
⇒ x + a = 0 or x + b = 0
∴ x = −a or x = −b
Q18. Find the roots of the following equation:
Sol. We have: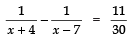
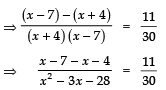
⇒ − 11 × 30 = 11 × (x2 − 3x − 28)
⇒ − 30 = x2 − 3x − 28
⇒ x2 − 3x − 28 + 30 = 0
⇒ x2 − 3x + 2 = 0
⇒ x2 − 2x − x + 2 = 0
⇒ x (x − 2) − 1 (x − 2)= 0
⇒ (x − 1) (x − 2) = 0
Either x −1= 0 ⇒ x = 1
or x −2 = 0 ⇒ x = 2
Thus, the required roots are: 1 and 2.
Q19. If α and β are roots of the equation x2 – 1 = 0, form an equation whose roots are
Sol. ∵ α and β are roots of x2 – 1 = 0 and x2 – 1 = 0 can be written as x2 + 0x – 1= 0 where a = 1, b = 0 and c = –1.
Now, the roots of the new equation are
∴ Sum of the roots of the new equation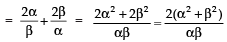
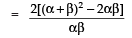
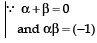
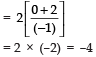
Product of the roots of the new equation
Since, a quadratic equation is given by
∴ The required quadratic equation is
x2 – (–4) x + 4 = 0
or x2 + 4x + 4 = 0
Remember α2 + β2 + 2αβ =(α + β)2
⇒ α2 + β2 =(α + β)2 – 2αβ
|
81 videos|339 docs|98 tests
|
FAQs on Class 10 Maths Chapter 4 Question Answers - Quadratic Equations
| 1. What is a quadratic equation? |  |
| 2. How do you solve a quadratic equation? |  |
| 3. Can a quadratic equation have more than two solutions? |  |
| 4. What is the discriminant of a quadratic equation? |  |
| 5. Can a quadratic equation have no solutions? |  |
















