Ex-15.3 (Part - 1), Areas Of Parallelograms And Triangles, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 1. In figure, compute the area of quadrilateral ABCD.
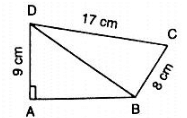
Solution:
Given:
DC = 17 cm, AD = 9 cm and BC = 8 cm
In ΔBCD we have
CD2 = BD2+BC2
⇒ 172 = BD2+82
⇒ BD2 = 289−64
⇒ BD = 15
In ΔABD we have
AB2+AD2 = BD2
⇒ 152 = AB2+92
⇒ AB2 = 225−81 = 144
⇒ AB = 12
ar(quadABCD) = ar(ΔABD)+ar(ΔBCD)
ar(quadABCD) =  (12×9)+
(12×9)+ (8×17) = 54+68 = 122cm2
(8×17) = 54+68 = 122cm2
ar(quadABCD) =  (12×9)+
(12×9)+ (8×15) = 54+60 = 114cm2
(8×15) = 54+60 = 114cm2
Q2. In figure, PQRS is a square and T and U are, respectively, the midpoints of PS and QR . Find the area of ΔOTS if PQ = 8 cm.
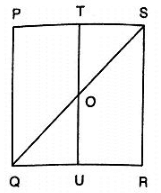
Solution:
From the figure,
T and U are mid points of PS and QR respectively
∴TU||PQ
⇒ TO||PQ
Thus , in ΔPQS , T is the mid point of PS and TO||PQ
∴TO =  PQ = 4cm
PQ = 4cm
Also, TS =  PS = 4cm
PS = 4cm
∴ar(ΔOTS) =  (TO×TS) =
(TO×TS) =  (4×4)cm2 = 8cm2
(4×4)cm2 = 8cm2
Q3. Compute the area of trapezium PQRS in figure
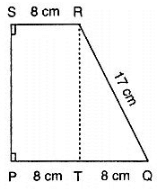
Solution:
We have,
ar(trap.PQRS) = ar(rect.PSRT)+ar(ΔQRT)
⇒ ar(trap.PQRS) = PT×RT+ (QT×RT)
(QT×RT)
= = 8×RT+ (8×RT) = 12×RT
(8×RT) = 12×RT
In ΔQRT , we have
QR2 = QT2+RT2
⇒ RT2 = QR2−QT2
⇒ RT2 = 172−82 = 225
⇒ RT = 15
Hence , area of trapezium = 12×15cm2 = 180cm2
Q4. In figure, ∠AOB = 90∘ , AC = BC , OA = 12 cm and OC = 6.5 cm .Find the area of ΔAOB.
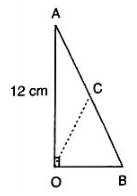
Solution:
Since, the midpoint of the hypotenuse of a right triangle is equidistant from the vertices
∴CA = CB = OC
⇒ CA = CB = 6.5cm
⇒ AB = 13cm
In right angled triangle OAB , we have
AB2 = OB2+OA2
⇒ 132 = OB2+122
⇒ OB2 = 132−122 = 169–144 = 25
⇒ OB = 5
∴ar(ΔAOB) =  (12×5) = 30cm2
(12×5) = 30cm2
Q5. In figure, ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm , and distance between AB and DC is 4 cm . Find the value of x and area of trapezium ABCD.
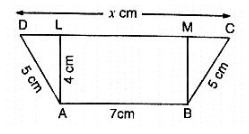
Solution:
Draw AL ⊥ DC, BM ⊥ DC then ,
AL = BM = 4 cm and LM = 7 cm.
In Δ ADL , we have
AD2 = AL2+DL2
⇒ 25 = 16+DL2
⇒ DL = 3cm
Similarly, MC = 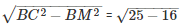
∴x = CD = CM+ML+LD = (3+7+3)cm = 13 cm
ar(trap.ABCD) =  (AB+CD)×AL =
(AB+CD)×AL =  (7+13)×4cm2 = 40cm2
(7+13)×4cm2 = 40cm2
Q 6. In figure, OCDE is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If OE = 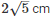 , find the area of the rectangle .
, find the area of the rectangle .
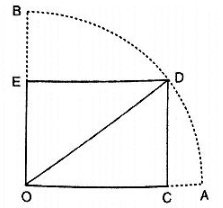
Solution:
Given OD = 10 cm and OE = 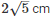
By using Pythagoras theorem
∴OD2 = OE2+DE2
⇒ DE = 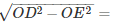
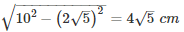
∴ Area of rectangle OCDE = OE×DE = 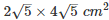 = 40cm2
= 40cm2
Q 7. In figure, ABCD is a trapezium in which AB || DC. Prove that ar(ΔAOD) = ar(ΔBOC)
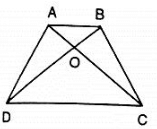
Solution:
Given: ABCD is a trapezium in which AB || DC
To prove: ar(ΔAOD) = ar(ΔBOC)
Proof:- Since , ΔADC and ΔBDC are on the same base DC and between same parallels AB and DC
Then, ar(ΔADC) = ar(ΔBDC)
⇒ ar(ΔAOD)+ar(ΔDOC) = ar(ΔBOC)+ar(ΔDOC)
⇒ ar(ΔAOD) = ar(ΔBOC)
Q 8. In figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ΔADE) = ar(ΔBCF).
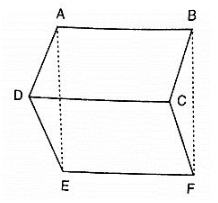
Solution:
Given that
ABCD is parallelogram ⇒ AD = BC
CDEF is parallelogram ⇒ DE = CF
ABFE is parallelogram ⇒ AE = BF
Thus, in Δs ADF and BCF , we have
AD = BC, DE = CF and AE = BF
So, by SSS criterion of congruence, we have
ΔADE≅ΔBCF
ar(ΔADE) = ar(ΔBCF)
Q 9. Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that : ar(ΔAPB)×ar(ΔCPD) = ar(ΔAPD)×ar(ΔBPC).
Solution:
Construction: – Draw BQ ⊥AC and DR ⊥ AC
Proof:-
L.H.S
= ar(ΔAPB)×ar(ΔCDP)
=  [(AP×BQ)]×(
[(AP×BQ)]×( ×PC×DR)
×PC×DR)
= ( ×PC×BQ)×(
×PC×BQ)×( ×AP×DR)
×AP×DR)
= ar(ΔAPD)×ar(ΔBPC).
= R.H.S
Hence proved.
Q 10. In figure, ABC and ABD are two triangles on the base AB. If line segment CD is bisected by AB at O, show that ar(ΔABC) = ar(ΔABD).
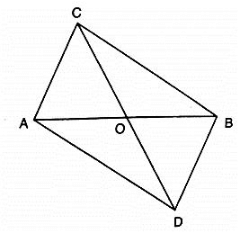
Solution:
Given that CD is bisected by AB at O
To prove: ar(ΔABC) = ar(ΔABD).
Construction: Draw CP ⊥ AB and DQ ⊥ AB .
Proof:
ar(ΔABC) =  ×AB×CP⋅⋅⋅⋅⋅⋅⋅(1)
×AB×CP⋅⋅⋅⋅⋅⋅⋅(1)
ar(ΔABD) =  ×AB×DQ⋅⋅⋅⋅⋅⋅⋅(2)
×AB×DQ⋅⋅⋅⋅⋅⋅⋅(2)
In ΔCPO and ΔDQO
∠CPO = ∠DQO [each90∘]
Given that, CO = OD
∠COP = ∠DOQ [Vertically opposite angles are equal]
Then , ΔCP0≅ΔDQO [By AAS condition]
∴CP = DQ (3) [c.p.c.t]
Compare equation (1), (2) and (3)
∴ ar(ΔABC) = ar(ΔABD).
Q 11. If P is any point in the interior of a parallelogram ABCD , then prove that area of the triangle APB is less than half the area of parallelogram.
Solution:
Draw DN ⊥ AB and PM ⊥ AB
Now ,
ar(||gmABCD) = AB×DN,ar(ΔAPB) =  (AB×PM)
(AB×PM)
Now , PM < DN
⇒ AB×PM<AB×DN
⇒  (AB×PM)<
(AB×PM)< (AB×DN)
(AB×DN)
⇒ ar(ΔAPB)< ar(||gmABCD)
ar(||gmABCD)
Q 12. If AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in area. If G is the mid-point of the median AD, prove that ar(ΔBGC) = 2ar(ΔAGC).
Solution:
Draw AM ⊥ BC
Since, AD is the median of ΔABC
∴ BD = DC
⇒ BD = AM = DC×AM
⇒  (BD×AM) =
(BD×AM) =  (DC×AM)
(DC×AM)
⇒ ar(ΔABD) = ar(ΔACD)⋅⋅⋅⋅⋅⋅⋅⋅⋅(1)
In ΔBGC , GD is the median
∴ ar(ΔBGD) = ar(ΔCGD)⋅⋅⋅⋅⋅⋅⋅⋅⋅(2)
In ΔACD , CG is the median
∴ ar(ΔAGC) = ar(ΔCGD)⋅⋅⋅⋅⋅⋅⋅⋅⋅(3)
From (2) and (3) we have,
ar(ΔBGD) = ar(ΔAGC)
But, ar(ΔBGC) = 2ar(ΔBGD)
∴ ar(ΔBGC) = 2ar(ΔAGC)
Q 13. A point D is taken on the side BC of a ΔABC , such that BD = 2DC . Prove that ar(ΔABD) = 2ar(ΔADC).
Solution:
Given that,
In ΔABC, BD = 2DC
To prove: ar(ΔABD) = 2ar(ΔADC).
Construction:
Take a point E on BD such that BE = ED
Proof: Since, BE = ED and BD = 2 DC
Then, BE = ED = DC
We know that median of triangle divides it into two equal triangles.
∴ In ΔABD , AE is the median .
Then , ar(ΔABD) = 2ar(ΔAED) ⋅⋅⋅⋅⋅⋅(1)
In ΔAEC , AD is the median .
Then, ar(ΔAED) = 2ar(ΔADC) ⋅⋅⋅⋅⋅⋅(2)
Compare equation 1 and 2
ar(ΔABD) = 2ar(ΔADC).
Q 14. ABCD is a parallelogram whose diagonals intersect at O .If P is any point on BO, prove that :
(i) . ar(ΔADO) = ar(ΔCDO).
(ii) . ar(ΔABP) = 2ar(ΔCBP).
Solution:
Given that ABCD is the parallelogram
To Prove: (i) ar(ΔADO) = ar(ΔCDO).
(ii) ar(ΔABP) = 2ar(ΔCBP).
Proof: we know that diagonals of parallelogram bisect each other
∴ AO = OC and BO = OD
(i) . In Δ DAC , since DO is a median .
Then ar(ΔADO) = ar(ΔCDO).
(ii) . In Δ BAC , since BO is a median .
Then ar(ΔBAO) = ar(ΔBCO)⋅⋅⋅⋅⋅⋅⋅(1)
In Δ PAC , since PO is a median .
Then ar(ΔPAO) = ar(ΔPCO)⋅⋅⋅⋅⋅⋅⋅(2)
Subtract equation 2 from 1.
⇒ ar(ΔBAO)−ar(ΔPAO) = ar(ΔBCO)−ar(ΔPCO)
⇒ ar(ΔABP) = 2ar(ΔCBP).
Q 15. ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F.
(i) . Prove that ar(ΔADF) = ar(ΔECF).
(ii) . If the area of ΔDFB = 3cm2 , find the area of ||gm ABCD .
Solution:
In triangles ADF and ECF, we have
∠ADF = ∠ECF [Alternate interior angles,SinceAD||BE]
AD = EC [sinceAD = BC = CE]
And ∠DFA = ∠CFA [Vertically opposite angles]
So, by AAS congruence criterion, we have
ΔADF≅ΔECF
⇒ ar(ΔADF) = ar(ΔECF) and DF = CF .
Now, DF = CF
⇒ BF is a median in Δ BCD.
⇒ ar(ΔBCD) = 2ar(ΔBDF)
⇒ ar(ΔBCD) = 2×3cm2 = 6cm2
Hence, area of a parallelogram = 2ar(ΔBCD) = 2×6cm2 = 12cm2
Q 16. ABCD is a parallelogram whose diagonals AC and BD intersect at O . A line through O intersects AB at P and DC at Q. Prove that ar(ΔPOA) = ar(ΔQOC).
Solution:
In triangles POA and QOC, we have
∠AOP = ∠COQ
AO = OC
∠PAC = ∠QCA
So, by ASA congruence criterion , we have
ΔPOA≅ΔQOC
⇒ ar(ΔPOA) = ar(ΔQOC).
Q 17. ABCD is a parallelogram. E is a point on BA such that BE = 2EA and F is point on DC such that DF = 2FC. Prove that AECF is a parallelogram whose area is one third of the area of parallelogram ABCD.
Solution:
Draw FG ⊥ AB
We have,
BE = 2 EA and DF = 2FC
⇒ AB – AE = 2 AE and DC – FC = 2 FC
⇒ AB = 3 AE and DC = 3 FC
⇒ AE = 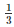 AB and FC =
AB and FC = 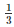 DC⋅⋅⋅⋅⋅⋅⋅⋅(1)
DC⋅⋅⋅⋅⋅⋅⋅⋅(1)
But AB = DC
Then, AE = FC [opposite sides of ||gm]
Thus, AE = FC and AE || FC
Then, AECF is a parallelogram
Now, area of parallelogram AECF = AE×FG
⇒ ar(||gmAECF) = 13AB×FG from(1)
⇒ 3ar(||gmAECF) = AB×FG ⋅⋅⋅⋅⋅(2)
Andar(||gmABCD) = AB×FG ⋅⋅⋅⋅⋅(3)
Compare equation 2 and 3
⇒ 3ar(||gmAECF) = ar(||gmABCD)
⇒ ar(||gmAECF) = 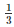 ar(||gmABCD)
ar(||gmABCD)
Q 18. In a triangle ABC, P and Q are respectively the mid points of AB and BC and R is the mid point of AP. Prove that :
(i) . ar(ΔPBQ) = ar(ΔARC).
(ii) . ar(ΔPRQ) =  ar(ΔARC).
ar(ΔARC).
(iii) . ar(ΔRQC) = 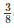 ar(ΔABC).
ar(ΔABC).
Solution:
We know that each median of a triangle divides it into two triangles of equal area.
(i) . Since CR is the median of Δ CAP
∴ar(ΔCRA) =  ar(ΔCAP)⋅⋅⋅⋅⋅⋅⋅(1)
ar(ΔCAP)⋅⋅⋅⋅⋅⋅⋅(1)
Also , CP is the median of a Δ CAB
∴ar(ΔCAP) = ar(ΔCPB)⋅⋅⋅⋅⋅⋅⋅(2)
From 1 and 2 , we get
∴ar(ΔARC) =  ar(ΔCPB)⋅⋅⋅⋅⋅⋅⋅(3)
ar(ΔCPB)⋅⋅⋅⋅⋅⋅⋅(3)
PQ is the median of a Δ PBC
∴ar(ΔCPB) = 2ar(ΔPBQ)⋅⋅⋅⋅⋅⋅⋅(4)
From 3 and 4, we get
∴ar(ΔARC) = ar(ΔPBQ)⋅⋅⋅⋅⋅⋅⋅(5)
(ii) . Since QP and QR medians of triangles QAB and QAP respectively
∴ar(ΔQAP) = ar(ΔQBP)⋅⋅⋅⋅⋅⋅⋅(6)
And ar(ΔQAP) = 2ar(ΔQRP)⋅⋅⋅⋅⋅⋅⋅(7)
From 6 and 7, we get
ar(ΔPRQ) =  ar(ΔPBQ)⋅⋅⋅⋅⋅⋅⋅(8)
ar(ΔPBQ)⋅⋅⋅⋅⋅⋅⋅(8)
From 5 and 8, we get
ar(ΔPRQ) =  ar(ΔARC)
ar(ΔARC)
(iii) . Since, LR is a median of Δ CAP
∴ar(ΔARC) =  ar(ΔCAD)
ar(ΔCAD)
=  ×
× ar(ΔABC)
ar(ΔABC)
= 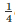 ar(ΔABC)
ar(ΔABC)
Since RQ is the median of Δ RBC.
∴ar(ΔRQC) =  ar(ΔRBC)
ar(ΔRBC)
=  {ar(ΔABC)−ar(ΔARC)}
{ar(ΔABC)−ar(ΔARC)}
=  {ar(ΔABC)−
{ar(ΔABC)−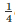 ar(ΔABC)}
ar(ΔABC)}
= 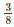 ar(ΔABC)
ar(ΔABC)
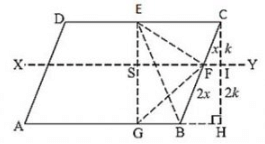
Q 19. ABCD is a parallelogram. G is a point on AB such that AG = 2GB and E is point on DC such that CE = 2DE and F is the point of BC such that BF = 2FC. Prove that:
(i) . ar(ADEG) = ar(GBCE).
(ii) . ar(ΔEGB) = 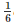 ar(ABCD).
ar(ABCD).
(iii) . ar(ΔEFC) =  ar(ΔEBF).
ar(ΔEBF).
(iv) . ar(ΔEGB) = 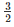 ×ar(ΔEFC)
×ar(ΔEFC)
(v) . Find what portion of the area of parallelogram is the area of Δ EFG.
Solution:
Given: ABCD is a parallelogram
AG = 2 GB, CE = 2 DE and BF = 2 FC
To prove:
(i) . ar(ADEG) = ar(GBCE).
(ii) . ar(ΔEGB) = 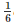 ar(ABCD).
ar(ABCD).
(iii) . ar(ΔEFC) =  ar(ΔEBF).
ar(ΔEBF).
(iv) . ar(ΔEGB) = 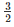 ×ar(ΔEFC)
×ar(ΔEFC)
(v) . Find what portion of the area of parallelogram is the area of Δ EFG.
Construction: Draw a parallel line to AB through point F and a perpendicular line to AB from C
Proof:
(i) .Since ABCD is a parallelogram
So, AB = CD and AD = BC
Consider the two trapezium s ADEG and GBCE
Since AB = DC, EC = 2DE, AG = 2GB
⇒ ED = 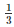 CD =
CD = 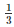 AB and EC =
AB and EC = 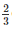 CD = 23AB
CD = 23AB
⇒ AG = 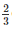 AB and BG =
AB and BG = 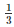 AB
AB
So , DE+AG = 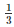 AB +
AB +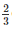 AB = AB and EC+BG =
AB = AB and EC+BG = 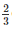 AB +
AB +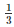 AB = AB
AB = AB
Since the two trapezium ADEG and GBCE have same height and their sum of two parallel sides are equal
Since Area of trapezium = 
So, ar(ADEG) = ar(GBCE).
(ii) . Since we know from above that
BG =  AB. So
AB. So
ar(ΔEGB) =  ×GB×Height
×GB×Height
ar(ΔEGB) =  ×
×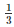 ×AB×Height
×AB×Height
ar(ΔEGB) = 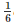 ×AB×Height
×AB×Height
ar(ΔEGB) = 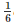 ar(ABCD).
ar(ABCD).
(iii) . Since height if triangle EFC and EBF are equal.So
ar(ΔEFC) =  ×FC×Height
×FC×Height
ar(ΔEFC) =  ×
× ×FB×Height
×FB×Height
ar(ΔEFC) =  ar(EBF)
ar(EBF)
Hence , ar(ΔEFC) =  ar(ΔEBF).
ar(ΔEBF).
(iv) . Consider the trapezium in which
ar(EGBC) = ar(ΔEGB)+ar(ΔEBF)+ar(ΔEFC)
⇒  ar(ABCD) =
ar(ABCD) = 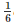 ar(ABCD)+2ar(ΔEFC)+ar(ΔEFC)
ar(ABCD)+2ar(ΔEFC)+ar(ΔEFC)
⇒ 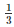 ar(ABCD) = 3ar(ΔEFC)
ar(ABCD) = 3ar(ΔEFC)
⇒ ar(ΔEFC) = 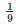 ar(ABCD)
ar(ABCD)
Now from (ii)part we have
ar(ΔEGB) = 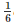 ar(ΔEFC)
ar(ΔEFC)
ar(ΔEGB) = 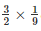 ar(ABCD)
ar(ABCD)
ar(ΔEGB) = 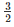 ar(ΔEFC)
ar(ΔEFC)
∴ar(ΔEGB) = 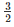 ar(ΔEFC)
ar(ΔEFC)
(v) . In the figure it is given that FB = 2CF .Let CF = x and FB = 2x.
Now consider the two triangles CFI and CBH which are similar triangle.
So by the property of similar triangle CI = k and IH = 2k
Now consider the triangle EGF in which
ar(ΔEFG) = ar(ΔESF)+ar(ΔSGF)
ar(ΔEFG) =  SF×k+
SF×k+ SF×2k
SF×2k
ar(ΔEFG) = 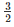 SF×k⋅⋅⋅⋅⋅(i)
SF×k⋅⋅⋅⋅⋅(i)
Now ,
ar(ΔEGBC) = ar(SGBF)+ar(ESFC)
ar(ΔEGBC) =  (SF+GB)×2k+
(SF+GB)×2k+ (SF+EC)×k
(SF+EC)×k
ar(ΔEGBC) = 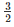 k×SF+(GB+
k×SF+(GB+ EC)×k
EC)×k
ar(ΔEGBC) = 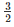 k×SF+(
k×SF+(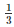 AB+
AB+ ×
×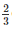 AB)×k
AB)×k
 ar(ΔABCD) =
ar(ΔABCD) = 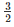 k×SF+
k×SF+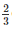 AB×k
AB×k
⇒ ar(ΔABCD) = 3k×SF+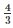 AB×k [Multiply both sides by 2]
AB×k [Multiply both sides by 2]
⇒ ar(ΔABCD) = 3k×SF+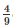 ar(ABCD)
ar(ABCD)
⇒ k×SF = 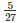 ar(ABCD)⋅⋅⋅⋅⋅⋅⋅(2)
ar(ABCD)⋅⋅⋅⋅⋅⋅⋅(2)
From 1 and 2 we have ,
ar(ΔEFG) =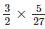 ar(ABCD)
ar(ABCD)
ar(ΔEFG) = 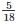 ar(ABCD)
ar(ABCD)
FAQs on Ex-15.3 (Part - 1), Areas Of Parallelograms And Triangles, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the formula to find the area of a parallelogram? |  |
| 2. How do you find the area of a triangle using the base and height? |  |
| 3. Can the area of a parallelogram be negative? |  |
| 4. Is the formula for finding the area of a parallelogram the same as that of a rectangle? |  |
| 5. How is the area of a triangle related to the area of a parallelogram? |  |


















