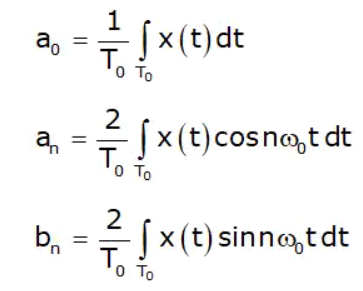Fourier Series Representation of Continuous Periodic Signals | Signals and Systems - Electrical Engineering (EE) PDF Download
Fourier Series Representation
The Periodic functions are the functions which can define by relation f(t + P) = f(t) for all t. For example, if f(t) is the amount of time between sunrise and sunset at a certain latitude, as a function of time t, and P is the length of the year, then f(t + P) = f(t) for all t, since the Earth and Sun are in the same position after one full revolution of the Earth around the Sun.
 f(t + P) = f(t) for all t
f(t + P) = f(t) for all t
Fourier Theorem
Any arbitrary continuous-time signal x(t) which is periodic with a fundamental period To, can be expressed as a series of harmonically related sinusoids whose frequencies are multiples of fundamental frequency or first harmonic.
In other words, any periodic function of (t) can be represented by an infinite series of sinusoids called as Fourier Series.
Periodic waveform expressed in the form of Fourier series, while non-periodic waveform may be expressed by the Fourier transform.
The different forms of Fourier series are given as follows:
(i) Trigonometric Fourier series
(ii) Complex exponential Fourier series
(iii) Polar or harmonic form Fourier series
Trigonometric Fourier Series
Any arbitrary periodic function x(t) with fundamental period T0 can be expressed as follows:
 ...(i)
...(i)
This is referred to as trigonometric Fourier series representation of signal x(t). Here, ω0 = 2π/T0 is the fundamental frequency of x(t) and coefficients a0, an, and bn are referred to as the trigonometric continuous-time Fourier series (CTFS) coefficients. The coefficients are calculated as follows:
(a) Fourier Series Coefficient
From equation (i), it is clear that coefficient a0 represents the average or mean value (also referred to as the dc component) of signal x(t).
In these formulas, the limits of integration are either (–T0/2 to +T0/2) or (0 to T0). In general, the limit of integration is any period of the signal and so the limits can be from (t1 to t2 + T0), where t1 is any time instant.
(b) Trigonometric Fourier Series Coefficients for Symmetrical Signals
If the periodic signal x(t) possesses some symmetry, then the continuous-time Fourier series (CTFS) coefficients become easy to obtain. The various types of symmetry and simplification of Fourier series coefficients are discussed as below.
Consider the Fourier series representation of a periodic signals x(t) defined in the equation: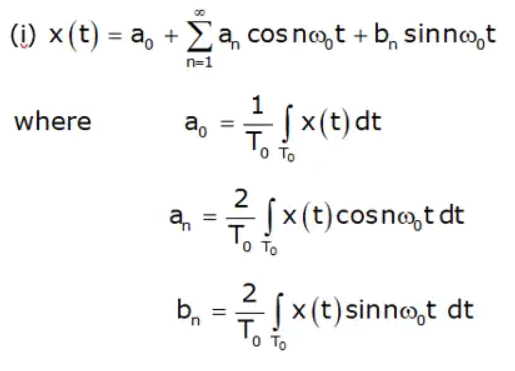
I. Even Symmetry: x(t) = x(–t)
 If x(t) is an even function, then product x(t) sinωot is odd and integration in equation (iv)
If x(t) is an even function, then product x(t) sinωot is odd and integration in equation (iv)
becomes zero. That is bn = 0 for all n and the Fourier series representation expressed as: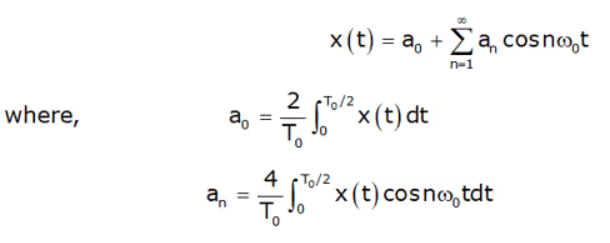
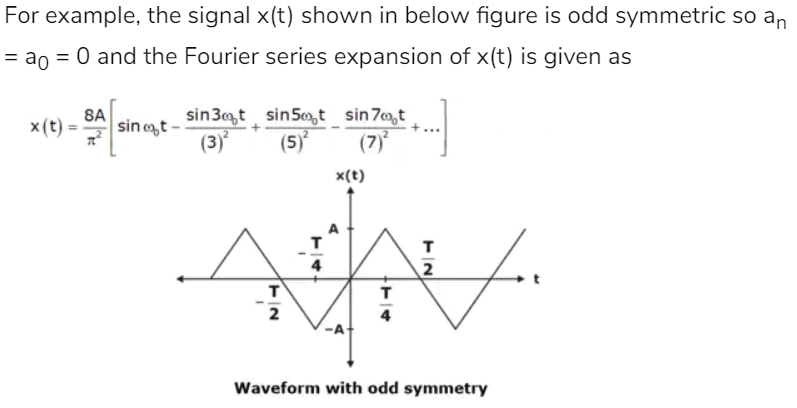
For example, the signal x(t) shown in below figure has even symmetry so bn = 0 and the
Fourier series expansion of x(t) is given as:
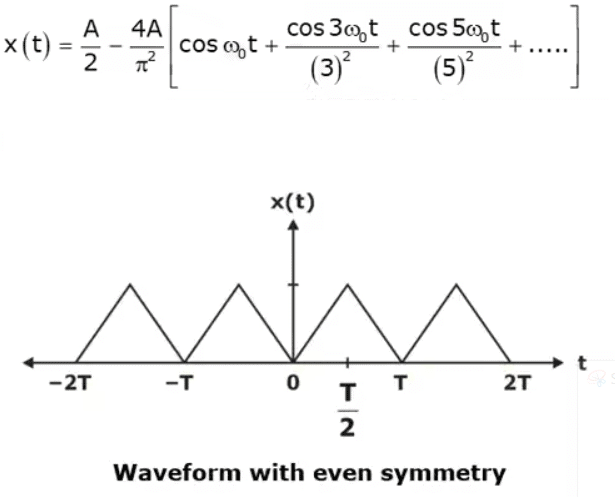
The trigonometric Fourier series representation even signals contains cosine terms only. The constant a0 may or may not be zero.
II. Odd Symmetry: x(t) = –x(–t)
If x(t) is an odd function, then product x(t) cosωot is also odd and integration in equation (iii) becomes zero i.e. an = 0 for all n. Also, a0 = 0 because an odd symmetric function has a zero average value. The Fourier series representation is expressed as: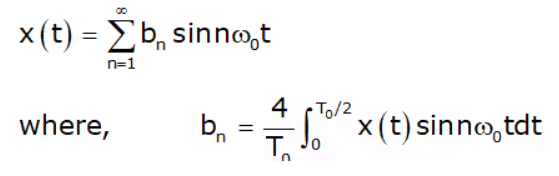
Complete Fourier Series
 -------(1)
-------(1)
- where a0, a1,... and b1, b2 . . . called Fourier coefficients & are computed as
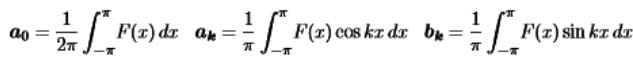
- The above is called the Fourier series for the function.That is, sines and cosines, the simplest periodic functions, are the “building blocks" for more general periodic functions.
- There are some terminology coming from acoustics and music: the n = 1 called the fundamental, and the frequencies n ≥ 2 are called the higher harmonics.
- cos(nt) and sin(nt) are periodic on the interval 2π for any integer n. The an and bn coefficients measure the strength of contribution from each "harmonic".
(a) Fourier Sine Series
The Fourier Sine series can be written as:
S(x) = b1 sinx + b2 sin 2x + b3 sin 3x + 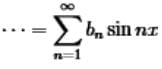 ........(2)
........(2)
- Sum S(x) will inherit all three properties:
(i) Periodic S(x +2π) = S(x)
(ii) Odd S(−x) = −S(x)
(iii) S(0) = S(π) = 0 - Our first step is to compute from S(x) the number bk that multiplies sinkx.
Suppose S(x) = ∑ bn sinnx. Multiply both sides by sin kx. Integrate from 0 to π in Sine Series in equation (2)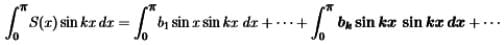
- On the right side, all integrals are zero except for n = k. Here the property of “orthogonality” will dominate. The sines make 90o angles in function space, when their inner products are integrals from 0 to π.
- Orthogonality for sine Series
Orthogonality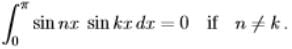 .........(3)
.........(3) - Zero comes quickly if we integrate the term comx from 0 to π. ⇒ 0∫π comx dx = 0-0=0
- Integrating cosmx with m = n−k and m = n + k proves orthogonality of the sines.
- The exception is when n = k. Then we are integrating (sinkx)2 = 1/2 − 1/2 cos2kx
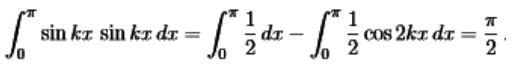
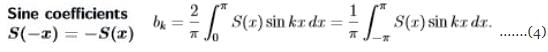
- Notice that S(x)sinkx is even (equal integrals from −π to 0 and from 0 to π).
- We will immediately consider the most important example of a Fourier sine series. S(x) is an odd square wave with SW(x) = 1 for 0<x<π. It is an odd function with period 2 π, that vanishes at x = 0 and x = π.
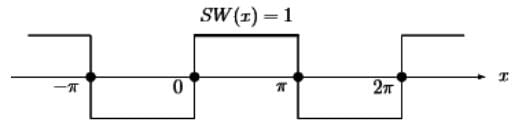
Example: Finding the Fourier sine coefficients bk of the square wave SW(x) as given above .
Solution:
For k =1 ,2,...using the formula of sine coefficient with S(x)=1 between 0 and π: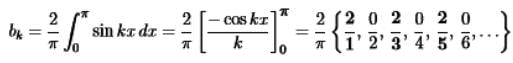
- Then even-numbered coefficients b2k are all zero because cos2kπ = cos0 = 1.
- The odd-numbered coefficients bk = 4/πk decrease at the rate 1/k.
- We will see that same 1/k decay rate for all functions formed from smooth pieces and jumps. Put those coefficients 4/πk and zero into the Fourier sine series for SW(x).

(b) Fourier Cosine Series
The cosine series applies to even functions with C(−x) = C(x) as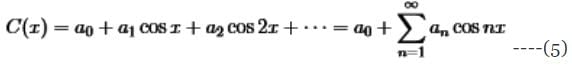
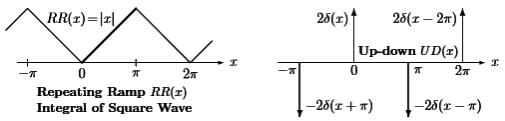
Cosine has period 2π shown as above in the figure two even functions, the repeating ramp RR(x) and the up-down train UD(x) of delta functions.
- That sawtooth ramp RR is the integral of the square wave. The delta functions in UD give the derivative of the square wave. RR and UD will be valuable examples, one smoother than SW, one less smooth.
- First we find formulas for the cosine coefficients a0 and ak. The constant term a0 is the average value of the function C(x):
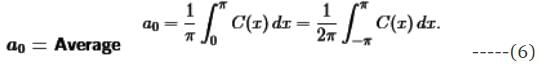
- We will integrate the cosine series from 0 to π. On the right side, the integral of a0 = a0π (divide both sides by π). All other integrals are zero.
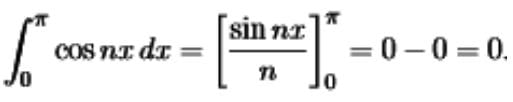
- Again the integral over a full period from −π to π (also 0 to 2π) is just doubled.
Orthogonality Relations of Fourier Series
Since from the Fourier Series Representation we concluded that for a periodic Signal it can be written as: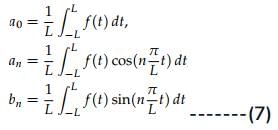
The condition of orthogonality as follow: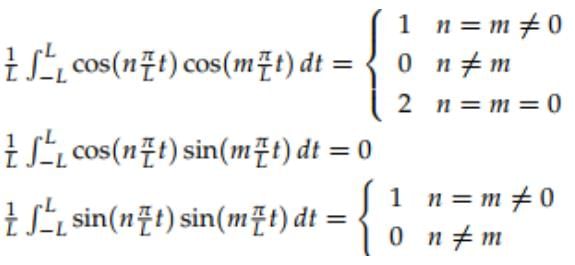
Proof of the orthogonality relations: This is just a straightforward calculation using the periodicity of sine and cosine and either (or both) of these two methods:

- Method 2: use the trig identity
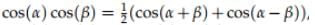 and the similar trig identies for cos(α) sin(β) and sin(α) sin(β).
and the similar trig identies for cos(α) sin(β) and sin(α) sin(β).
Energy in Function = Energy in Coefficients
There is also another important equation (the energy identity) that comes from integrating (F(x))2. When we square the Fourier series of F(x), and integrate from −π to π, all the “cross terms” drop out. The only nonzero integrals come from 12 and cos2 kx and sin2 kx, multiplied by a02,ak2 bk2.
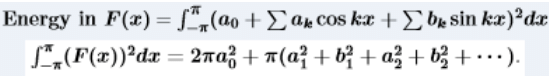
- Energy in F(x) equals the energy in the coefficients.
- Left hand side is like the length squared of a vector, except the vector is a function.
- Right hand side comes from an infinitely long vector of a’s and b’s.
- If the lengths are equal, which says that the Fourier transform from function to vector is like an orthogonal matrix.
- Normalized by constants √2π and √π, we have an orthonormal basis in function space.
Complex Fourier Series
- In place of separate formulas for a0 and ak and bk, we may consider one formula for all the complex coefficients Ck.
- So that the function F(x) will be complex, The Discrete Fourier Transform will be much simpler when we use N complex exponentials for a vector.
Here we practice in advance with the complex infinite series for a 2π-periodic function: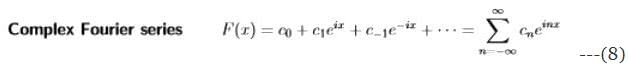
- If every cn = c−n, we can combine einx with e−inx into 2cosnx. Then last equation is the cosine series for an even function.
- If every cn =−c−n, we use einx−e−inx =2i sinnx. Then last equation is sine series for an odd function and the c’s are pure imaginary.
- To find ck, multiply (8) by e−ikx (not eikx) and integrate from −π to π.
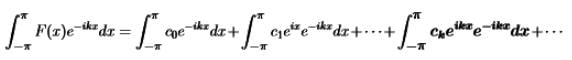
- Since the complex exponentials are orthogonal. Every integral on the right side is zero, except for the term (when n = k and (eikx)(e−ikx)= 1). The integral of 1 is 2π.which only term gives the formula for ck.
- Since c0 = a0 is still the average of F(x), because e0 = 1.
- The orthogonality of einx and eikx is to be checked by integrating.
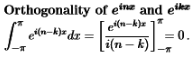
Example: Compute the Fourier series of f(t), where f(t) is the square wave with period 2π. which is defined over one period by.
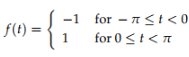 The graph over several periods is shown below.
The graph over several periods is shown below.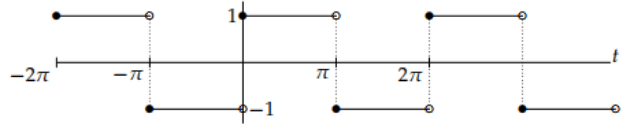
Solution: Computing a Fourier series means computing its Fourier coefficients. We do this using the integral formulas for the coefficients given with Fourier’s theorem in the previous note. For convenience we repeat the theorem here.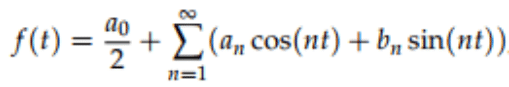
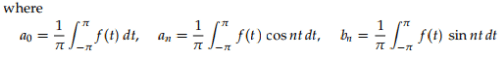
By applying these formulas to the above waveform we have to split the integrals into two pieces corresponding to where f(t) is +1 and where it is −1.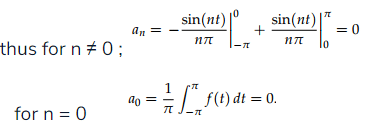
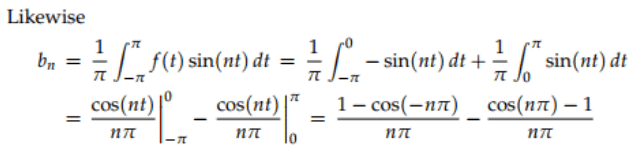
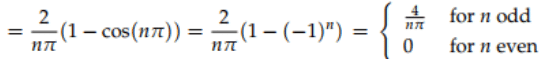
We have used the simplification cos nπ = (−1)n to get a nice formula for the coefficients bn.
This then gives the Fourier series for f(t)
|
45 videos|70 docs|33 tests
|
FAQs on Fourier Series Representation of Continuous Periodic Signals - Signals and Systems - Electrical Engineering (EE)
| 1. What is the Fourier series representation? |  |
| 2. What is the Fourier theorem? |  |
| 3. What is the difference between trigonometric and complex Fourier series? |  |
| 4. What are the orthogonality relations of Fourier series? |  |
| 5. How does the energy in a function relate to the energy in its Fourier coefficients? |  |