Class 9 Exam > Class 9 Notes > Mathematics (Maths) Class 9 > Short Notes - Introduction to Euclid's Geometry
Introduction to Euclid’s Geometry Class 9 Notes Maths Chapter 5

Introduction
Geometry, a mathematical discipline exploring various shapes and sizes prevalent in our daily experiences, was revolutionized by the Greek mathematician Euclid. In this chapter's introduction to Euclid's geometry, we delve into the foundations laid by Euclid, encompassing new definitions, axioms, and postulates that form the basis of contemporary geometry.
 Euclid
Euclid
Euclid's Definitions, Axioms and Postulates
- Euclid was a Greek mathematician, who introduced the method of proving a geometrical result by using logical reasonings on previously proved and known results.
- The statement is a sentence that can be judged to be true or false.
- A Theorem is a statement that requires proof.
Note: Proving a theorem means establishing the truth of that theorem.
- The corollary is a statement whose truth can easily be deduced from a theorem.
- Axioms are the basic facts that are taken for granted without proof.
- Postulates are the basic facts that are taken for granted specific to geometry, without proof.
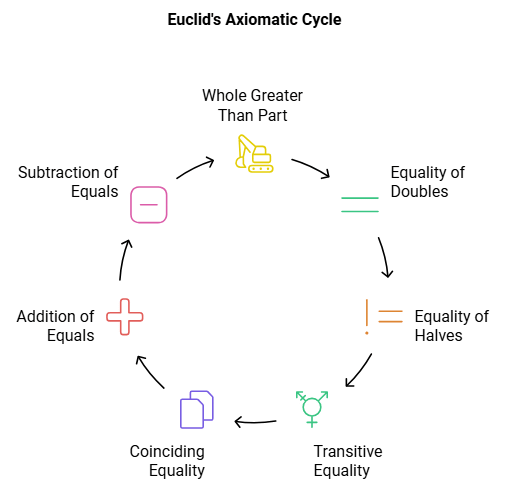
Some of Euclid’s axioms are:
- The whole is greater than the part.
- Things which are double of the same things are equal to one another.
- Things which are halves of the same things are equal to one another.
- Things which are equal to the same thing are equal to one another.
- Things which coincide with one another are equal to one another.
- If equals are added to equals, the wholes are equal.
- If equals are subtracted from equals, the remainders are equal.

Note:
- Euclidean Geometry is the study of flat surfaces.
- Nowadays ‘postulates’ and ‘axioms’ are terms that are used interchangeably and in the same sense.
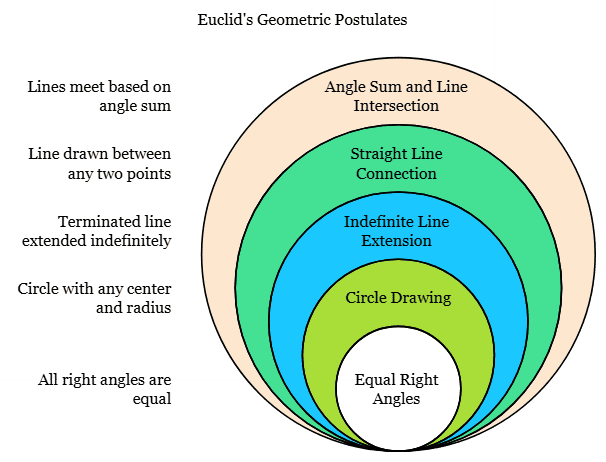
Euclid's Five Postulates
- Postulate 1: A straight line may be drawn from any point to any other point.
- Postulate 2: A terminated line can be produced indefinitely.
- Postulate 3: A circle can be drawn with any center and any radius.
- Postulate 4: All right angles are equal to one another.
- Postulate 5: If a straight line falling on two straight lines makes the interior angles on the same side of it taken together is less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of the angles is less than two right angles.
Example: The straight line PQ falls on AB and CD such that the sum of the interior angles 1 and 2 is less than 180º on the left side of PQ. Thus, the lines AB and CD will intersect (on producing) on the left side of PQ.
The document Introduction to Euclid’s Geometry Class 9 Notes Maths Chapter 5 is a part of the Class 9 Course Mathematics (Maths) Class 9.
All you need of Class 9 at this link: Class 9
|
40 videos|471 docs|57 tests
|
FAQs on Introduction to Euclid’s Geometry Class 9 Notes Maths Chapter 5
| 1. What are axioms in Euclid's Geometry? |  |
Ans. Axioms in Euclid's Geometry are fundamental statements or principles that are accepted without proof. They serve as the foundation for all other geometric reasoning and deductions.
| 2. How are Euclid's Definitions, Axioms, and Postulates related? |  |
Ans. Euclid's Definitions, Axioms, and Postulates are all essential components of his geometric system. Definitions establish the meaning of basic terms, axioms provide the fundamental principles, and postulates are specific assumptions used to prove geometric theorems.
| 3. What is the purpose of Euclid's Axioms? |  |
Ans. Euclid's Axioms serve as the starting points for reasoning in his geometry. They are the assumptions upon which all geometric proofs and deductions are based. These axioms ensure the logical consistency and validity of Euclidean geometry.
| 4. Can Euclid's Axioms be proven? |  |
Ans. Euclid's Axioms are accepted without proof and are assumed to be self-evident truths. They cannot be proven within the system of Euclidean geometry itself but are considered as foundational principles that are intuitively true.
| 5. How do Euclid's Axioms contribute to geometric reasoning? |  |
Ans. Euclid's Axioms provide a set of logical principles that allow for the deduction of new geometric properties and theorems. They serve as the starting points for reasoning and enable the systematic development of Euclidean geometry.
Related Searches






















