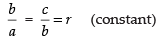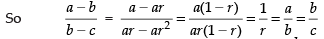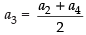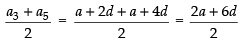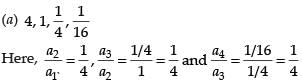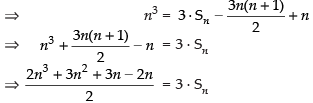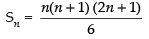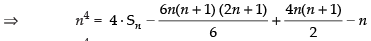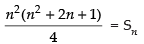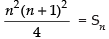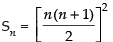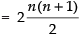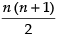Q.1. The first term of an A.P.is a, and the sum of the first p terms is zero, show that the sum of its next q terms is
[Hint: Required sum = Sp + q – Sp]
Ans.
Given that a1 = a and Sp = 0
Sum of next q terms of the given A.P. = Sp+q – Sp
∴ 
and 
⇒ 2a + (p – 1)d = 0 ⇒ (p – 1)d = – 2a
⇒
Sum of next q terms = Sp+q – Sp


Hence, the required sum =
Q.2. A man saved Rs 66000 in 20 years. In each succeeding year after
the first year he saved Rs 200 more than what he saved in the previous
year. How much did he save in the first year?
Ans.
Let ₹ x be saved in first year.
Annual increment = ₹ 200
which forms an A.P.
first term = a and common difference d = 200
n = 20 years
∴ 
⇒ 66000 = 10[2a + 3800] ⇒ 6600 = 2a + 3800
⇒ 2a = 6600 - 3800 ⇒ 2a = 2800 ⇒ a = 1400 Hence, the man saved ₹1400 in the first year.
Q.3. A man accepts a position with an initial salary of Rs 5200 per month. It is understood that he will receive an automatic increase of Rs 320 in the very next month and each month thereafter.
(a) Find his salary for the tenth month
(b) What is his total earnings during the first year?
Ans.
Given that fixed increment in the salary of a man
=₹ 320 each
month Initial salary = ₹ 5200 which makes an A.P.
whose first term (a) = ₹ 5200 and common difference (d) = ₹ 320
(i) Salary for the tenth month
a10 = a + (n – 1)d
= 5200 + (10 – 1) x 320 = 5200 + 2880 = ₹ 8080
(ii) Total earning during the first year (12 months)

= 6[10400 + 3520] = 6 x 13920 = ₹ 83520
Hence, the required amount is (i) ₹ 8080 (ii) ₹ 83520.
Q.4. If the pth and qth terms of a G.P. are q and p respectively, show that its (p + q)th term is
Ans.
Let a be the first term and r be the common ratio of a G.P.
Given that ap = q ⇒ arp–1 = q ...(i)
and aq = p ⇒ arq–1 = p ...(ii)
Dividing eq. (i) by eq. (ii) we get,

putting the value of r in eq. (i), we get


Now Tp+q = arp+q–1 =


Hence, the required term =
Q.5. A carpenter was hired to build 192 window frames. The first day he made five frames and each day, thereafter he made two more frames than he made the day before. How many days did it take him to finish the job?
Ans.
Here, first term a = 5 and the common difference d = 2
let the carpenter will take n days to finish the job
Sn = 192

⇒ 192 x 2 = n[10 + 2n - 2] ⇒ 384 = n(2n + 8)
⇒ 384 = 2n2 + 8n ⇒ 2n2 + 8n - 384 = 0
⇒ n2 + 4n – 192 = 0 ⇒ n2 + 16n – 12n – 192 = 0
⇒ n(n + 16) – 12 (n + 16) = 0 ⇒ (n - 12) (n + 16) = 0
⇒ n = 12 [∵ n ≠ –16]
Hence, the required number of days = 12.
Q.6. We know the sum of the interior angles of a triangle is 180°. Show that the sums of the interior angles of polygons with 3, 4, 5, 6, ... sides form an arithmetic progression. Find the sum of the interior angles for a 21 sided polygon.
Ans.
Since, the sum of all interior angles of a polygon of n sides
= (2n – 4) x 90°
∴ Sum of interior angles of a polygon of sides 3
= (2 x 3 - 4) x 90° = 180°
Sum of interior angles of a polygon of sides 4
= (2 x 4 - 4) x 90° = 360°
Similarly, the sum of interior angles of the polygon of sides, 5, 6, 7 … are 540°, 720°, 900°…
Therefore, the series will be 180°, 360°, 540°, 720°, 900°…
which is A.P.
Here a = 180°, d = 180°
We have to find the sum of interior angles of a polygon of 21 sides i.e. 19th term
an = a + (n – 1)d
a19 = 180° + (19 – 1)180° = 180° + 18 x 180°
= 180° + 3240° = 3420°
Hence, the required sum of interior angles = 3420°.
Q.7. A side of an equilateral triangle is 20cm long. A second equilateral triangle is inscribed in it by joining the mid points of the sides of the first triangle. The process is continued as shown in the accompanying diagram. Find the perimeter of the sixth inscribed equilateral triangle.
Ans.
The side of the first equilateral DABC = 20 cm
By joining the mid points of the sides of this triangle, we get the second equilateral triangle which each side

[∴ The line joining the mid-points of two sides of a triangle
is 1/2 and parallel to third side of the triangle]
Similarly each side of the third equilateral triangle =
∴ Perimeter of first triangle = 20 x 3 = 60 cm
Perimeter of the second triangle = 10 x 3 = 30 cm
and the perimeter of the third triangle = 5 x 3 = 15 cm
Therefore, the series will be 60, 30, 15,
which is G.P. in which a = 60, and r =
Now, we have to find the perimeter of the sixth inscribed equilateral triangle
∴ a6 = ar6–1
=
Hence, the required perimeter =
Q.8. In a potato race 20 potatoes are placed in a line at intervals of 4 meters with the first potato 24 meters from the starting point. A contestant is required to bring the potatoes back to the starting place one at a time. How far would he run in bringing back all the potatoes?
Ans.
As per the given information we have the following diagram

Starting point = S Distance traveled to bring the first potato = 24 + 24 = 48 m Distance traveled to bring the second potato = 2(24 + 4) = 56 m
Distance traveled to bring the third potato = 2(24 + 4 + 4) = 64 m Therefore, the series will be = 48, 56, 64, …
which an A.P. in which a = 48, d = 56 – 48 = 8
We have to find the total distance to bring all the potatoes
back, so, n = 20
∴ 
⇒
= 10 x 248 = 2480 m
Hence, the required distance = 2480 m
Q.9. In a cricket tournament 16 school teams participated. A sum of Rs 8000 is to be awarded among themselves as prize money. If the last placed team is awarded Rs 275 in prize money and the award increases by the same amount for successive finishing places, how much amount will the first place team receive?
Ans.
Let the prize amount got by first place team be ₹ a
Since, the prize money increases by the same amount for successive finishing places, therefore the series will be A.P.
∴ an = 275, n = 16 and S16 = 8000
an = a + (n – 1)d
275 = a + (16 – 1)(– d)
[∴ Common difference d is (-) as the series is decreasing]
⇒ 275 = a - 15d ...(i)

⇒ 8000 = 8[2a – 15d] ⇒ 2a - 15d = 1000 ...(ii)
Solving eq. (i) and eq. (ii) we get
a = 725 and d = 30
Hence, the required award received by first place term =₹ 725.
Q.10. If a1, a2, a3, ..., an are in A.P., where ai > 0 for all i, show that

Ans.
Given that a1, a2, a3, a4, …, an are in A.P.
∴ Common difference d = a2 - a1 = a3 - a2 = a4 - a3 = ... = an - an-1


Adding the above terms, we get


Now an = a1 + (n – 1)d
⇒ an – a1 = (n – 1)d
 ...(ii)
...(ii)
From Eq. (i) and eq. (ii) we get

Hence proved.
Q.11. Find the sum of the series
(33 – 23) + (53 – 43) + (73 – 63) + ... to (i) n terms (ii) 10 terms
Ans.
Given series
⇒ (33 - 23) + (53 - 43) + (73 - 63) + ...
= (33 + 53 + 73 + …) – (23 + 43 + 63 + …)
⇒ [33 + 53 + 73 + ... (2n + 1)3] - [23 + 43 + 63 + ... (2n)3]
∴ Tn = (2n + 1)3 – (2n)3
= (2n + 1 - 2n) [(2n + 1)2 + (2n + 1) (2n) + (2n)2 ]
[∴ a3 - b3 = (a - b) (a2 + ab + b2)]
= 1 × [4n2 + 1 + 4n + 4n2 + 2n + 4n2]
= 12n2 + 6n + 1
(i) 

= 2n(n + 1) (2n + 1) + 3n(n + 1) + n
= n[2(n + 1) (2n + 1) + 3(n + 1) + 1]
= n[2(2n2 + 3n + 1) + 3n + 3 + 1]
= n[4n2 + 6n + 2 + 3n + 4]
= n[4n2 + 9n + 6]
= 4n3 + 9n2 + 6n
(ii) S10 = 4(10)3 + 9(10)2 + 6(10) = 4 x 1000 + 900 + 60
= 4000 + 960 = 4960
Q.12. Find the rth term of an A.P. sum of whose first n terms is 2n + 3n2.
[Hint: an = Sn – Sn–1]
Ans.
Given that Sn = 2n + 3n2
⇒ S1 = 2 x 1 + 3(1)2 = 5
⇒ S2 = 2 x 2 + 3 x 4 = 16
⇒ S3 = 2 x 3 + 3 x 9 = 33
… … …
∴ S1 = a1 = 5
S2 - S1 = a2 = 16 - 5 = 11
∴ d = a2 – a1 = 11 – 5 = 6
Now Tr = a1 + (r – 1)d
= 5 + (r – 1)6 = 5 + 6r – 6 = 6r – 1
Hence, the required rth term is 6r – 1
Long Answer Type
Q.13. If A is the arithmetic mean and G1, G2 be two geometric means between any two numbers, then prove that

Ans.
Let the two numbers be x and y
∴  ...(i)
...(i)
If G1 and G2 be the geometric means between x and y then x, G1, G2, y are in G.P.
Then y = xr4–1 [∴ an = arn–1]

Now 
and 

= x + y = 2A LHS. [using eq. (i)]
∴ LHS = RHS
Hence proved.
Q.14. If θ1, θ2, θ3, ..., θn are in A.P., whose common difference is d, show that secθ1 secθ2 + secθ2 secθ3 + ... + secθn–1 secθn
Ans.
Since θ1, θ2, θ3, …, θn are in A.P.
∴ θ2 – θ1 = θ3 – θ2 = … = θn – θn–1 = d
Now we have to prove that
sec θ1 × sec θ2 + sec θ2 × sec θ3 + ... + sec θn-1 . sec θn

Taking only

Similarly we can solve other terms which will be

Here LHS =

LHS = RHS
Hence proved.
Q.15. If the sum of p terms of an A.P. is q and the sum of q terms is p, show that the sum of p + q terms is – (p + q). Also, find the sum of first p – q terms (p > q).
Ans.
Let a be the first term and d the common difference of the given A.P.

Subtracting eq. (ii) from eq. (i) we get

Substituting the value of d in eq. (i) we get



Hence proved.
Q.16. If pth, qth, and rth terms of an A.P. and G.P. are both a, b and c respectively, show that ab–c . bc – a . ca – b = 1
Ans.
Let A and d be the first term and common difference respectively of an A.P. and x and R be the first term and common ratio respectively of the G.P.
∴ A + (p – 1)d = a ...(i)
A + (q – 1)d = b ...(ii)
and A + (r – 1)d = c ...(iii)
For G.P., we have
xRp–1 = a ...(iv)
xRq–1 = b ...(v)
and xRr–1 = c ...(vi)
Subtracting eq. (ii) from eq. (i) we get
(p – q)d = a – b ...(vii)
Similarly, (q – r)d = b – c ...(viii)
and (r – p)d = c – a ...(ix)
Now we have to prove that
ab–c × bc–a × ca–b = 1
L.H.S. ab–c × bc–a × ca–b
= [ xR p -1 ]( q - r) d × [xR q-1 ]( r- p)d× [ xR r -1 ]( p - q)d [from (i), (ii), (iii), (iv), (v), (vi), (vii), (viii), (ix)]
= x(q-r)d × R(p-1) (q-r)d × x(r-p)d × R(q-1) (r-p)d × x(p-q)d × R(r-1) (p-q)d
= x(q-r)d + (r-p)d + (p-q)d R(p-1)(q-r)d + (q-1) (r-p)d + (r-1) (p-q)d
= x(q-r+r-p+p-q)d × R(pq-pr-q+r+qr-pq-r+p+pr-qr-p+q)d
= x(0)d × R(0)d = x0 × R0 = 1 R.H.S.
L.H.S. = R.H.S.
Hence proved.
Objective Type Questions
Q.17. If the sum of n terms of an A.P. is given by Sn = 3n + 2n2, then the common difference of the A.P. is
(a) 3
(b) 2
(c) 6
(d) 4
Ans. (d)
Solution.
Given that Sn = 3n + 2n2
S1 = 3(1) + 2(1)2 = 5
S2 = 3(2) + 2(4) = 14
S1 = a1 = 5
S2 – S1 = a2 = 14 – 5 = 9
∴ Common difference d = a2 - a1 = 9 - 5 = 4
Hence, the correct option is (d).
Q.18. The third term of G.P. is 4. The product of its first 5 terms is
(a) 43
(b) 44
(c) 45
(d) None of these
Ans. (c)
Solution.
Given that T3 = 4
⇒ ar3–1 = 4 [∴ Tn = arn-1]
⇒ ar2 = 4
Product of first 5 terms = a × ar × ar2 × ar3 × ar4
= a5r10 = (ar2)5 = (4)5
Hence, the correct option is (c).
Q.19. If 9 times the 9th term of an A.P. is equal to 13 times the 13th term, then the 22nd term of the A.P. is
(a) 0
(b) 22
(c) 220
(d) 198
Ans. (a)
Solution.
Tn = a + (n – 1)d
∴ T9 = a + 8d
and T13 = a + 12d
As per the given condition
9[a + 8d] = 13[a + 12d]
⇒ 9a + 72d = 13a + 156d ⇒ - 4a = 84d
⇒ a = – 21d ...(i)
Now T22 = a + 21d = – 21d + 21d = 0 [from eq. (i)]
Hence, the correct option is (a).
Q.20. If x, 2y, 3z are in A.P., where the distinct numbers x, y, z are in G.P. then the common ratio of the G.P. is
(a) 3
(b)1/3
(c) 2
(d)1/2
Ans. (b)
Solution.
Since x, 2y, 3z are in A.P.
∴ 2y – x = 3z –2y
⇒ 4y = x + 3z ...(i)
Now x, y, z are in G.P.
∴ Common ratio r =
∴ y2 = xz
putting the value of x from eq. (i), we get
y2 = (4y – 3z)z ⇒ y2 = 4yz – 3z2
⇒ 3z2 – 4yz + y2 = 0 ⇒ 3z2 - 3yz - yz + y2 = 0
⇒ 3z(z - y) - y(z - y) = 0 ⇒ (3z - y) (z - y) = 0
⇒ 3z – y = 0 and z – y = 0
⇒ 3z = y and z ≠ y
[∴ z and y are distinct numbers]
⇒  (from eq. (ii))
(from eq. (ii))
Hence, the correct option is (b).
Q.21. If in an A.P., Sn = q n2 and Sm = qm2, where Sr denotes the sum of r terms of the A.P., then Sq equals
(a)q3/2
(b) mnq
(c) q3
(d) (m + n) q2
Ans. (c)
Solution.
The given series is A.P. whose first term is a and common difference is d
∴ 
⇒ 2a + (n – 1)d = 2qn ...(i)

⇒ 2a + (m – 1)d = 2qm ...(ii)
Solving eq. (i) and eq. (ii) we get

(m – n)d = 2qm – 2qn
(m – n)d = 2q(m – n)
∴ d = 2q
Putting the value of d in eq. (ii) we get
2a + (m – 1) × 2q = 2qm ⇒ 2a = 2qm - (m -1)2q
⇒ 2a = 2q(m - m + 1) ⇒ 2a = 2q ⇒ a = q

Hence, the correct option is (c).
Q.22. Let Sn denote the sum of the first n terms of an A.P.
If S2n = 3Sn then S3n : Sn is equal to
(a) 4
(b) 6
(c) 8
(d) 10
Ans. (b)
Solution.

∴

As per the condition of the question, we have
S2n = 3 × Sn
⇒ 
⇒ 2[2a + (2n – 1)d] = 3[2a + (n – 1)d]
⇒ 4a + (4n – 2)d = 6a + (3n – 3)d
⇒ 6a + (3n – 3)d – 4a – (4n – 2)d = 0
⇒ 2a + (3n – 3 – 4n + 2)d = 0 ⇒ 2a + (- n - 1)d = 0
⇒ 2a – (n + 1)d = 0 ⇒ 2a = (n + 1)d (i)


Hence, the correct option is (b).
Q.23. The minimum value of 4x + 41–x , x ∈ R, is
(a) 2
(b) 4
(c) 1
(d) 0
Ans. (b)
Solution.
We know that AM ≥ GM

Hence, the correct option is (b).
Q.24. Let Sn denote the sum of the cubes of the first n natural numbers and sn denote the sum of the first n natural numbers. Then equals
equals
(a)
(b)
(c)
(d)None of these
Ans. (a)
Solution.
Given that
Let Tn be the nth term of the above series

Now sum of the given series

Hence, the correct option is (a).
Q.25. If tn denotes the nth term of the series 2 + 3 + 6 + 11 + 18 + ... then t50 is
(a) 492 – 1
(b) 492
(c) 502 + 1
(d) 492 + 2
Ans. (d)
Solution.
Let Sn = 2 + 3 + 6 + 11 + 18 + … + t50
Using method of difference, we get
Sn = 2 + 3 + 6 + 11 + 18 + … + t50 ...(i)
and Sn = 0 + 2 + 3 + 6 + 11 + … + t49 + t50 ...(ii)
Subtracting eq. (ii) from eq. (i), we get
0 = 2 + 1 + 3 + 5 + 7 + … – t50 terms
⇒ t50 = 2 + (1 + 3 + 5 + 7 + … upto 49 terms)

Hence, the correct option is (d).
Q.26. The lengths of three unequal edges of a rectangular solid block are in G.P. The volume of the block is 216 cm3 and the total surface area is 252 cm2. The length of the longest edge is
(a) 12 cm
(b) 6 cm
(c) 18 cm
(d) 3 cm
Ans. (a)
Solution.
Let the length, breadth and height of a rectangular block be
 a and ar. [Since they are is G.P]
a and ar. [Since they are is G.P]
∴ Volume = l x b x h

⇒ a3 = 216 ⇒ a = 6
Now total surface area = 2[lb + bh + lh]


⇒ 2r2 – 5r + 2 = 0 ⇒ 2r2 – 4r – r + 2 = 0
⇒ 2r(r – 2) –1(r – 2) = 0 ⇒ (r - 2) (2r - 1) = 0
⇒ r – 2 = 0 and 2r – 1 = 0
∴
Therefore, the three edge are:
If r = 2 then edges are 3, 6, 12
If r = then edges are 12, 6, 3
then edges are 12, 6, 3
So, the length of the longest edge = 12
Hence, the correct option is (a).
Fill in the blanks
Q.27. For a, b, c to be in G.P. the value of is equal to .............. .
is equal to .............. .
Ans.
Since a, b and c are in G.P
∴ 
⇒ b = ar and c = br ⇒ c = ar × r = ar2

Hence, the correct value of the filler is
Q.28. The sum of terms equidistant from the beginning and end in an A.P. is equal to ............ .
Ans.
Let A.P be a, a + d, a + 2d, a + 3d, …, a + (n – 1)d
Taking first and last term
a1 + an = a + a + (n – 1)d = 2a + (n – 1)d
Taking second and second last term
a2 + an–1 = (a + d) + [a + (n – 2)d] = 2a + (n – 1)d = a1 + an
Taking third from the beginning and the third from the end
a3 + an–2 = (a + 2d) + [a + (n – 3)d] = 2a + (n – 1)d = a1 + an
From the above pattern, we observe that the sum of terms
equidistant from the beginning and the end in an A.P is equal to the
[first term + last term]
Hence, the correct value of the filler is first term + last term.
Q.29. The third term of a G.P. is 4, the product of the first five terms is ................ .
Ans.
Given T3 = 4
∴ ar2 = 4 ...(i)
Product of first five terms = a × ar × ar2 × ar3 × ar4
= a5r10 = (ar2)5 = (4)5 [from eq. (i)]
Hence, the correct value of the fillter is (4)5.
TRUE/FALSE
Q.30. Two sequences cannot be in both A.P. and G.P. together.
Ans.
Let us consider aG.P, a , ar and ar2
If it is in A.P then ar – a ≠ ar2 – ar
Hence, the given statement is True.
Q.31. Every progression is a sequence but the converse, i.e., every sequence is also a progression need not necessarily be true.
Ans.
Let us consider a sequence of prime numbers 2, 3, 5, 7, 11, … It is clear that this progression is a sequence but sequence is not a progression because it does not follow a specific pattern.
Here, the given statement is True.
Q.32. Any term of an A.P. (except first) is equal to half the sum of terms which are equidistant from it.
Ans.
Let us consider an A.P a, a + d, a + 2d, …
∴ a2 + a4 = a + d + a + 3d = 2a + 4d = 2a3
⇒ 

⇒ = a + 3d = a4
Hence, the given statement is True.
Q.33. The sum or difference of two G.P.s, is again a G.P.
Ans. Let us consider two G.P.’s
a1 , a1r1 , a1r12 , a1r13 .... a1r1n-1
and a2 , a2 r2 , a2 r22 , a2 r23 ,.... a2 r2n-1
Now Sum of two G.Ps....
(a1 + a2 ) + (a1r1 + a2 r2 ) + (a1r12 + a2 r22 ).....

Now let us consider the difference G.P’s
( a1 - a2 ) + ( a1r1 - a2 r2 ) + ( a1r12 - a2 r22 )

Hence, the given statement is False.
Q.34. If the sum of n terms of a sequence is quadratic expression then it always represents an A.P.
Ans.
Let Sn = an2 + bn + c (quadratic expression)
S1 = a + b + c
∴ a1 = a + b + c
S2 = 4a + 2b + c
a2 = S2 – S1 = (4a + 2b + c) – (a + b + c) = 3a + b
S3 = 9a + 3b + c
⇒ a3 = S3 – S2 = (9a + 3b + c) – (4a + 2b + c) = 5a + b
Common difference d = a2 – a1 = (3a + b) – (a + b + c)
= 2a – c
and d = a3 – a2 = (5a + b) – (3a + b) = 2a
Here, we observe that a2 – a1 ≠ a3 – a2
So it does not represent an A.P
Hence, the given statement is False.
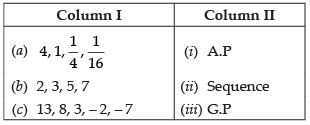
Q.35. Match the questions given under Column I with their appropriate answers given under the Column II.

Ans.

Hence it is G.P
∴ (a) ↔ (iii)
(b) 2, 3, 5, 7
Here a2 – a1 = 3 – 2 = 1
a3 – a2 = 5 – 3 = 2
∴ a2 – a1 ≠ a3 – a2
Hence it is not A.P
(c) 13, 8, 3, – 2, – 7
Here a2 – a1 = 8 – 13 = – 5
a3 – a2 = 3 – 8 = – 5
So, a2 – a1 = a3 – a2 = – 5
So, it is an A.P
Hence (c) ↔ (i)
Q.36.

Ans.
(a) Let Sn = 12 + 22 + 32 + … + n2
K3 – (K – 1)3 = 3K2 – 3K + 1
For K = 1, 13 – 03 = 3(1)2 – 3(1) + 1
For K = 2, 23 – 13 = 3(2)2 – 3(2) + 1
For K = 3, 33 – 23 = 3(3)2 – 3(3) + 1
For K = n, n3 – (n – 1)3 = 3(n)2 – 3(n) + 1
Adding Column wise, we get
n3 – 03 = 3(12 + 22 + 32 + … + n2)
– 3(1 + 2 + 3 + … +n) + n

⇒ 6 × Sn = 2n3 + 3n2 + n
⇒ 6 × Sn = n(2n2 + 3n + 1)
⇒ 6 × Sn = n[2n2 + 2n + n + 1]
⇒ 6 × Sn = n(n + 1) (2n + 1)
⇒
Here (a) ↔ (iii)
(b) Let Sn = 13 + 23 + 33 + … + n3
K4 – (K – 1)4 = 4K3 – 6K2 + 4K – 1
For K = 1, 14 – 04 = 4(1)3 – 6(1)2 + 4(1) – 1
For K = 2, 24 – 14 = 4(2)3 –6(2)2 + 4(2) – 1
For K = 3, 34 – 24 = 4(3)3 – 6(3)2 + 4(3) – 1
For K = n, n4 – (n –1)4 = 4(n)3 – 6(n2) + 4(n) – 1
Adding column wise, we get
⇒ n4 – 04 = 4(13 + 23 + 33 + … n3)
– 6(12 + 22 + 32 + … + n2)
+ 4(1 + 2 + 3 + … n) – n

⇒ n4 = 4 × Sn - n(n + 1) (2n + 1) + 2n(n + 1) - n
⇒ n4 + n(n + 1) (2n + 1) - 2n(n + 1) + n = 4 × Sn
⇒ n [n3 + (n + 1) (2n + 1) - 2n - 2 + 1] = 4 × Sn
⇒ n [n3 + 2n2 + 3n + 1 – 2n – 1] = 4 × Sn
⇒ n[n3 + 2n2 + n] = 4 × Sn
⇒
⇒
∴ 
Hence (b) ↔ (i)
(c) Let Sn = 2 + 4 + 6 + ....+ 2n
= 2(1 + 2 + 3 + .... + n)

= n(n + 1)
Hence (c) ↔ (ii)
(d) Let Sn = 1 + 2 + 3 +...+ n =
Hence (d) ↔ (iv)
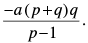
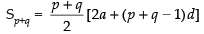
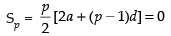
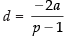
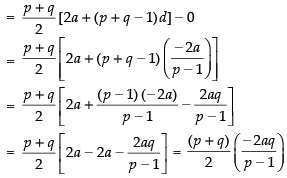
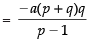
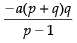
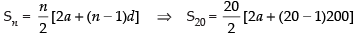
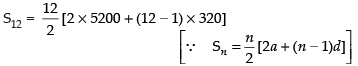
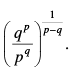
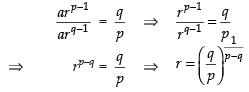

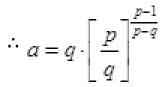
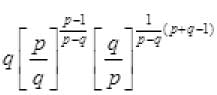
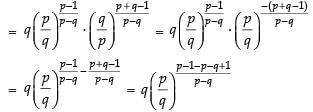
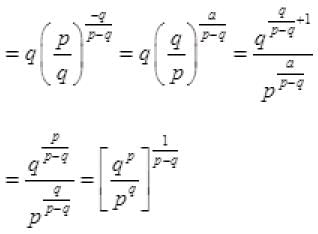
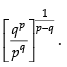
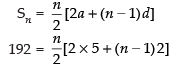
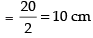
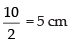
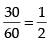
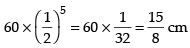
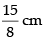


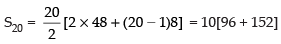
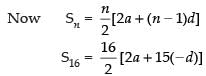
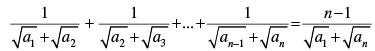
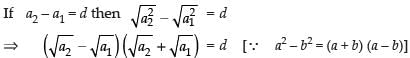

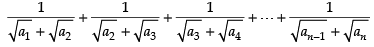
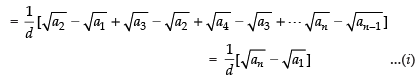
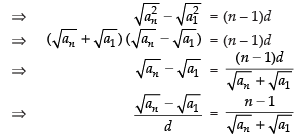 ...(ii)
...(ii)
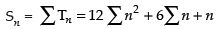
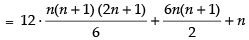
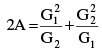
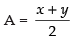 ...(i)
...(i)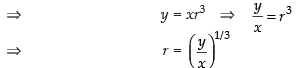
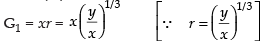
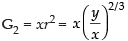
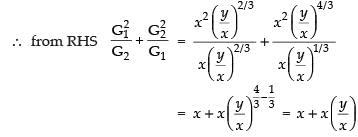
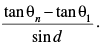
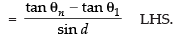
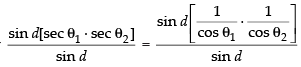
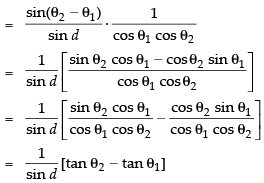
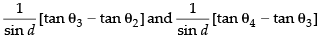
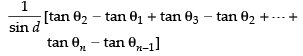
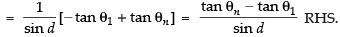
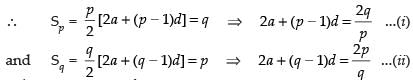
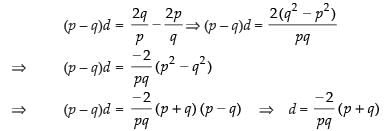
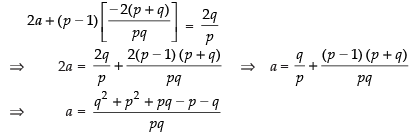

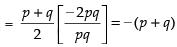
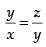
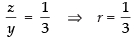 (from eq. (ii))
(from eq. (ii))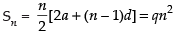

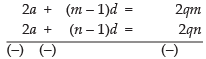

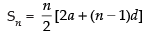
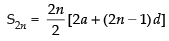
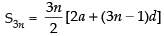
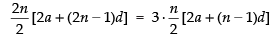
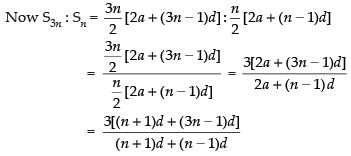
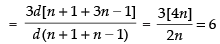
 equals
equals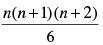
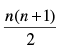
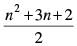
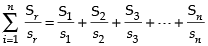

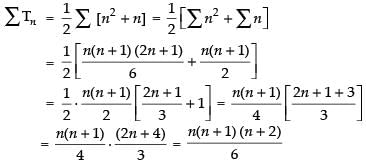
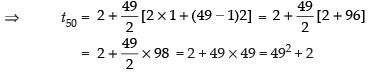
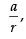 a and ar. [Since they are is G.P]
a and ar. [Since they are is G.P] 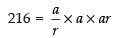
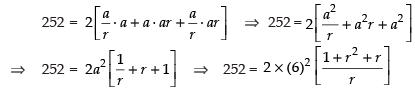
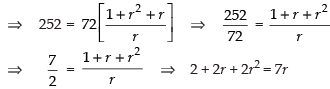
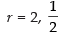
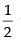 then edges are 12, 6, 3
then edges are 12, 6, 3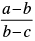 is equal to .............. .
is equal to .............. .