RD Sharma Solutions Ex-6.4, (Part -2), Factorization Of Polynomials, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q14. Find the values of a and b, if x2 – 4 is a factor of ax4+2x3–3x2+bx–4
Sol :
Given , f(x) = ax4+2x3–3x2+bx–4
g(x) = x2 – 4
first we need to find the factors of g(x)
⇒ x2 – 4
⇒ x2 = 4
⇒ x = √4
⇒ x = ±2
(x – 2) and (x + 2) are the factors
By factor therorem if (x – 2) and (x + 2) are the factors of f(x) the result of f(2) and f(-2) should be zero
Let , x – 2 = 0
⇒ x = 2
Substitute the value of x in f(x)
f(2) = a(2)4+2(2)3–3(2)2+b(2)–4
= 16a + 2(8) – 3(4) + 2b – 4
= 16a + 2b + 16 – 12 – 4
= 16a + 2b
Equate f(2) to zero
⇒ 16a + 2b = 0
⇒ 2(8a + b) = 0
⇒ 8a + b = 0 ———- 1
Let , x + 2 = 0
⇒ x = -2
Substitute the value of x in f(x)
f(-2) = a(−2)4+2(−2)3–3(−2)2+b(−2)–4
= 16a + 2(-8) – 3(4) – 2b – 4
= 16a – 2b – 16 – 12 – 4
= 16a – 2b – 32
= 16a – 2b – 32
Equate f(2) to zero
⇒ 16a – 2b – 32 = 0
⇒ 2(8a – b) = 32
⇒ 8a – b = 16 ———— 2
Solve equation 1 and 2
8a + b = 0
8a – b = 16
16a = 16
a = 1
substitute a value in eq 1
8(1) + b = 0
⇒ b = -8
The values are a = 1 and b = -8
Q15. Find α,β if (x + 1) and (x + 2) are the factors of x3+3x2−2αx+β
Sol:
Given, f(x) = x3+3x2−2αx+β and the factors are (x + 1) and (x + 2)
From factor theorem, if they are tha factors of f(x) then results of f(-2) and f(-1) should be zero
Let , x + 1 = 0
⇒ x = -1
Substitute value of x in f(x)
f(-1) = (−1)3+3(−1)2−2α(−1)+β
=−1+3+2α+β
= 2α+β + 2 ———— 1
Let , x + 2 = 0
⇒ x = -2
Substitute value of x in f(x)
f(-2) = (−2)3+3(−2)2−2α(−2)+β
=−8+12+4α+β
=4α+β + 4 ————– 2
Solving 1 and 2 i.e (1 – 2)
⇒2α+β+2–(4α+β + 4) = 0
⇒ −2α–2 = 0
⇒ 2α=−2
⇒ α = −1
Substitute α = -1 in equation 1
⇒ 2(−1)+β = -2
⇒ β = -2 + 2
⇒ β = 0
The values are α = −1 and β = 0
Q16. Find the values of p and q so that x4+px3+2x2−3x+q is divisible by (x2 – 1)
Sol :
Here , f(x) = x4+px3+2x2−3x+q
g(x) = x2–1
first, we need to find the factors of x2–1
⇒ x2–1 = 0
⇒ x2 = 1
⇒ x = ±1
⇒ (x + 1) and (x – 1)
From factor theorem , if x = 1, -1 are the factors of f(x) then f(1) = 0 and f(-1) = 0
Let us take , x + 1
⇒ x + 1 = 0
⇒ x = -1
Substitute the value of x in f(x)
f(-1) = (−1)4+p(−1)3+2(−1)2−3(−1)+q
= 1 – p + 2 + 3 + q
= -p + q + 6 ———- 1
Let us take , x – 1
⇒ x – 1 = 0
⇒ x = 1
Substitute the value of x in f(x)
f(1) = (1)4+p(1)3+2(1)2−3(1)+q
= 1 + p + 2 – 3 + q
= p + q ———- 2
Solve equations 1 and 2
-p + q = -6
p + q = 0
2q = -6
q = -3
substitute q value in equation 2
p + q = 0
p – 3 = 0
p = 3
the values of are p = 3 and q = -3
Q17. Find the values of a and b so that (x + 1) and (x – 1) are the factors of x4+ax3–3x2+2x+b
Sol :
Here, f(x) = x4+ax3–3x2+2x+b
The factors are (x + 1) and (x – 1)
From factor theorem , if x = 1, -1 are the factors of f(x) then f(1) = 0 and f(-1) = 0
Let , us take x + 1
⇒ x + 1 = 0
⇒ x = -1
Substitute value of x in f(x)
f(-1) = (−1)4+a(−1)3–3(−1)2+2(−1)+b
= 1 – a – 3 – 2 + b
= -a + b – 4 ——- 1
Let , us take x – 1
⇒ x – 1 = 0
⇒ x = 1
Substitute value of x in f(x)
f(1) = (1)4+a(1)3–3(1)2+2(1)+b
= 1 + a – 3 + 2 + b
= a + b ——- 2
Solve equations 1 and 2
-a + b = 4
a + b = 0
2b = 4
b = 2
substitute value of b in eq 2
a + 2 = 0
a = -2
the values are a = -2 and b = 2
Q18. If x3+ax2–bx+10 is divisible by x3–3x+2, find the values of a and b
Sol :
Here , f(x) = x3+ax2–bx+10
g(x) = x3–3x+2
first, we need to find the factors of g(x)
g(x) = x3–3x+2
= x3–2x–x+2
= x(x – 2) -1( x – 2)
= ( x – 1) and ( x – 2) are the factors
From factor theorem , if x = 1, 2 are the factors of f(x) then f(1) = 0 and f(2) = 0
Let, us take x – 1
⇒ x – 1 = 0
⇒ x = 1
Substitute the value of x in f(x)
f(1) = 13+a(1)2–b(1)+10
= 1 + a – b + 10
= a – b + 11 ——- 1
Let, us take x – 2
⇒ x – 2 = 0
⇒ x = 2
Substitute the value of x in f(x)
f(2) = 23+a(2)2–b(2)+10
= 8 + 4a – 2b + 10
= 4a – 2b + 18
Equate f(2) to zero
⇒ 4a – 2b + 18 = 0
⇒ 2(2a – b + 9) = 0
⇒ 2a – b + 9 ———- 2
Solve 1 and 2
a – b = -11
2a – b = -9
(-) (+) (+)
-a = -2
a = 2
substitute a value in eq 1
⇒ 2 – b = -11
⇒ – b = -11 – 2
⇒ -b = -13
⇒ b = 13
The values are a = 2 and b = 13
Q19. If both (x + 1) and (x – 1) are the factors of ax3+x2−2x+b , Find the values of a and b
Sol:
Here, f(x) = ax3+x2−2x+b
(x + 1) and (x – 1) are the factors
From factor theorem , if x = 1, -1 are the factors of f(x) then f(1) = 0 and f(-1) = 0
Let, x – 1= 0
⇒ x = -1
Substitute x value in f(x)
f(1) = a(1)3+(1)2−2(1)+b
= a + 1 – 2 + b
= a + b – 1 ———- 1
Let, x + 1= 0
⇒ x = -1
Substitute x value in f(x)
f(-1) = a(−1)3+(−1)2−2(−1)+b
= -a + 1 + 2 + b
= -a + b + 3 ———- 2
Solve equations 1 and 2
a + b = 1
-a + b = -3
2b = -2
⇒ b = -1
substitute b value in eq 1
⇒ a – 1 = 1
⇒ a = 1 + 1
⇒ a = 2
The values are a= 2 and b = -1
Q20. What must be added to x3–3x2–12x+19 so that the result is exactly divisible by x2+x–6
Sol :
Here , p(x) = x3–3x2–12x+19
g(x) = x2+x–6
by division algorithm, when p(x) is divided by g(x) , the remainder wiil be a linear expression in x
let, r(x) = ax + b is added to p(x)
⇒ f(x) = p(x) + r(x)
= x3–3x2–12x+19 + ax + b
f(x) = x3–3x2+x(a–12)+19 + b
We know that , g(x) = x2+x–6
First, find the factors for g(x)
g(x) = x2+3x–2x–6
= x(x + 3) -2(x + 3)
= (x + 3) ( x – 2) are the factors
From, factor theorem when (x + 3) and (x – 2) are the factors of f(x) the f(-3) = 0 and f(2) = 0
Let, x + 3 = 0
⇒ x = -3
Substitute the value of x in f(x)
f(-3) = (−3)3–3(−3)2+(−3)(a–12)+19 + b
= -27 – 27 – 3a + 24 + 19 + b
= -3a + b + 1 ——— 1
Let, x – 2 = 0
⇒ x = 2
Substitute the value of x in f(x)
f(2) = (2)3–3(2)2+(2)(a–12)+19 + b
= 8 – 12 + 2a – 24 + b
= 2a + b – 9 ——— 2
Solve equations 1 and 2
-3a + b = -1
2a + b = 9
(-) (-) (-)
-5a = – 10
a = 2
substitute the value of a in eq 1
⇒ -3(2) + b = -1
⇒ -6 + b = -1
⇒ b = -1 + 6
⇒ b = 5
∴ r(x) = ax + b
= 2x + 5
∴ x3–3x2–12x+19 is divided by x2+x–6 when it is added by 2x + 5
Q21. What must be added to x3–6x2–15x+80 so that the result is exactly divisible by x2+x–12
Sol :
Let, p(x) = x3–6x2–15x+80
q(x) = x2+x–12
by division algorithm, when p(x) is divided by q(x) the remainder is a linear expression in x.
so, let r(x) = ax + b is subtracted from p(x), so that p(x) – q(x) is divisible by q(x)
let f(x) = p(x) – q(x)
q(x) = x2+x–12
= x2+4x–3x–12
= x(x + 4) (-3)(x + 4)
= (x+4) , (x – 3)
clearly, (x – 3) and (x + 4) are factors of q(x)
so, f(x) wiil be divisible by q(x) if (x – 3) and (x + 4) are factors of q(x)
from , factor theorem
f(-4) = 0 and f(3) = 0
⇒ f(3) = 33–6(3)2–3(a+15)+80 – b = 0
= 27 – 54 -3a -45 + 80 –b
= -3a –b + 8 ——— 1
Similarly,
f(-4) = 0
⇒ f(-4) ⇒ (−4)3–6(−4)2–(−4)(a+15)+80 – b = 0
⇒ -64 – 96 -4a + 60 + 80 –b = 0
⇒ 4a – b – 20 = 0 ———- 2
Substract eq 1 and 2
⇒ 4a – b – 20 – 8 + 3a + b = 0
⇒ 7a – 28 = 0
⇒ a = 28/7
⇒ a= 4
Put a = 4 in eq 1
⇒ -3(4) – b = -8
⇒ -b – 12 = -8
⇒ -b = -8 + 12
⇒ b = -4
Substitute a and b values in r(x)
⇒ r(x) = ax + b
= 4x – 4
Hence, p(x) is divisible by q(x) , if r(x) = 4x – 4 is subtracted from it
Q22. What must be added to 3x3+x2–22x+9 so that the result is exactly divisible by 3x2+7x–6
Sol :
Let, p(x) = 3x3+x2–22x+9 and q(x) = 3x2+7x–6
By division theorem, when p(x) is divided by q(x) , the remainder is a linear equation in x.
Let, r(x) = ax + b is added to p(x) , so that p(x) + r(x) is divisible by q(x)
f(x) = p(x) + r(x)
⇒ f(x) = 3x3+x2–22x+9(ax+b)
⇒ = 3x3+x2+x(a–22)+b+9
We know that,
q(x) = 3x2+7x–6
= 3x2+9x–2x–6
= 3x(x+3) – 2(x+3)
= (3x-2) (x+3)
So, f(x) is divided by q(x) if (3x-2) and (x+3) are the factors of f(x)
From, factor theorem
f(2/3) = 0 and f(-3) = 0
let , 3x – 2 = 0
3x = 2
x = 2/3
⇒ f(2/3) = 3(2/3)3+(2/3)2 + (2/3)(a – 22) + b + 9
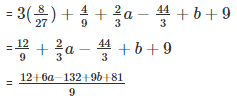
Equate to zero
⇒ 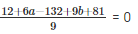
⇒ 6a + 9b – 39 = 0
⇒ 3(2a + 3b – 13) = 0
⇒ 2a + 3b – 13 = 0 ———- 1
Similarly,
Let, x + 3 = 0
⇒ x = -3
⇒ f(-3) = 3(−3)3+(−3)2+(−3)(a–22)+b+9
= -81 + 9 -3a + 66 + b + 9
= -3a + b + 3
Equate to zero
-3a + b + 3 = 0
Multiply by 3
-9a + 3b + 9 = 0 ——– 2
Substact eq 1 from 2
⇒ -9a + 3b + 9 -2a – 3b + 13 = 0
⇒ -11a + 22 = 0
⇒ -11a = -22
⇒ a = 22/11
⇒ a = 2
Substitute a value in eq 1
⇒ -3(2) + b = -3
⇒ -6 + b = -3
⇒ b = -3 + 6
⇒ b = 3
Put the values in r(x)
r(x) = ax + b
= 2x + 3
Hence, p(x) is divisible by q(x) , if r(x) = 2x + 3 is added to it
Q23. If x – 2 is a factor of each of the following two polynomials , find the value of a in each case :
1. x3–2ax2+ax–1
2. x5–3x4–ax3+3ax2+2ax+4
Sol :
(1) let f(x) = x3–2ax2+ax–1
from factor theorem
if (x – 2) is the factor of f(x) the f(2) = 0
let , x – 2 = 0
⇒ x = 2
Substitute x value in f(x)
f(2) = 23–2a(2)2+a(2)–1
= 8 – 8a + 2a – 1
= -6a + 7
Equate f(2) to zero
⇒ -6a + 7 = 0
⇒ -6a = -7
⇒ a= 76
When , (x – 2) is the factor of f(x) then a= 76
(2) Let, f(x) = x5–3x4–ax3+3ax2+2ax+4
from factor theorem
if (x – 2) is the factor of f(x) the f(2) = 0
let , x – 2 = 0
⇒ x = 2
Substitute x value in f(x)
f(2) = 25–3(2)4–a(2)3+3a(2)2+2a(2)+4
= 32 – 48 – 8a + 12 + 4a + 4
= 8a – 12
Equate f(2) to zero
⇒ 8a – 12 = 0
⇒ 8a = 12
⇒ a = 12/8
= 3/2
So, when (x – 2) is a factor of f(x) then a = 3/2
Q24. In each of the following two polynomials , find the value of a, if (x – a) is a factor :
1. x6–ax5+x4–ax3+3x–a+2
2. x5–a2x3+2x+a+1
Sol :
(1) x6–ax5+x4–ax3+3x–a+2
let , f(x) = x6–ax5+x4–ax3+3x–a+2
here , x – a = 0
⇒ x = a
Substitute the value of x in f(x)
f(a) = a6–a(a)5+(a)4–a(a)3+3(a)–a+2
= a6–a6+(a)4–a4+3(a)–a+2
= 2a + 2
Equate to zero
⇒ 2a + 2 = 0
⇒ 2(a + 1) = 0
⇒ a = -1
So, when (x – a) is a factor of f(x) then a = -1
(2) x5–a2x3+2x+a+1
let, f(x) = x5–a2x3+2x+a+1
here , x – a = 0
⇒ x = a
Substitute the value of x in f(x)
f(a) = a5–a2a3+2(a)+a+1
= a5–a5+2a+a+1
= 3a + 1
Equate to zero
⇒ 3a + 1 = 0
⇒ 3a = -1
⇒ a= −1/3
So, when (x – a) is a factor of f(x) then a = −1/3
Q25. In each of the following two polynomials , find the value of a, if (x + a) is a factor :
1. x3+ax2–2x+a+4
2. x4–a2x2+3x–a
Sol :
(1) x3+ax2–2x+a+4
let, f(x) = x3+ax2–2x+a+4
here , x + a = 0
⇒ x = -a
Substitute the value of x in f(x)
f(-a) = (−a)3+a(−a)2–2(−a)+a+4
= (−a)3+a3–2(−a)+a+4
= 3a + 4
Equate to zero
⇒ 3a + 4 = 0
⇒ 3a = -4
⇒ a = −4/3
So, when (x + a) is a factor of f(x) then a = −4/3
(2) x4–a2x2+3x–a
let, f(x) = x4–a2x2+3x–a
here , x + a = 0
⇒ x = -a
Substitute the value of x in f(x)
f(-a) = (−a)4–a2(−a)2+3(−a)–a
= a4–a4–3(a)–a
= -4a
Equate to zero
⇒ -4a = 0
⇒ a = 0
So, when (x + a) is a factor of f(x) then a = 0
FAQs on RD Sharma Solutions Ex-6.4, (Part -2), Factorization Of Polynomials, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the importance of factorization of polynomials in mathematics? |  |
| 2. How can factorization of polynomials be used to solve equations? |  |
| 3. What are the different methods of factorizing polynomials? |  |
| 4. Can all polynomials be factored? |  |
| 5. How is factorization of polynomials related to finding the roots of a polynomial equation? |  |





















