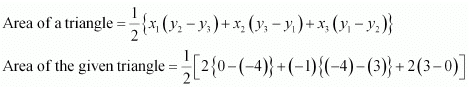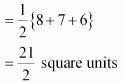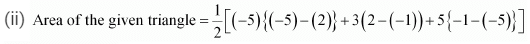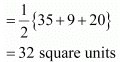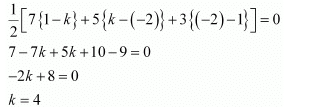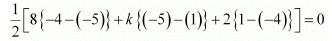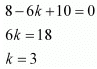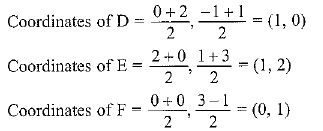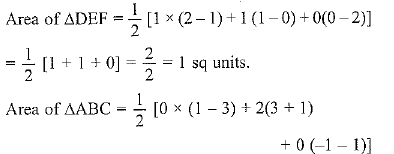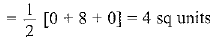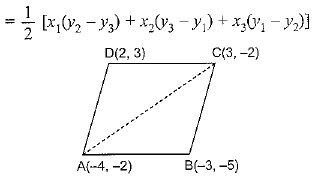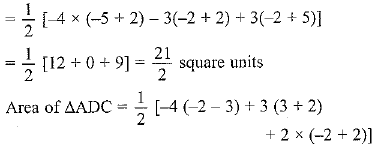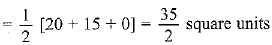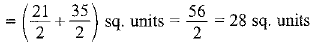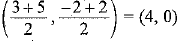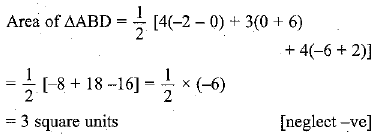Q.1. Find the area of the triangle whose vertices are:
(i) (2, 3), (−1, 0), (2, −4)
(ii) (−5, −1), (3, −5), (5, 2)
Sol. (i) Area of a triangle is given by
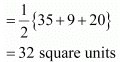
Q.2. In each of the following find the value of ‘k’, for which the points are collinear.
(i) (7, −2), (5, 1), (3, k)
(ii) (8, 1), (k, − 4), (2, −5)
Sol. (i) For collinear points, area of triangle formed by them is zero.
Therefore, for points (7, −2) (5, 1), and (3, k), area = 0
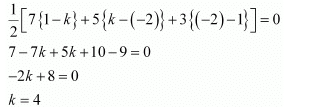
(ii) For collinear points, area of triangle formed by them is zero
Therefore, for points (8, 1), (k, −4), and (2, −5), area = 0
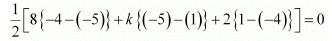
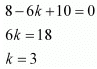
Q.3. Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, −1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
Sol. Let D, E and F are mid-points of the sides AB, BC and AC respectively.
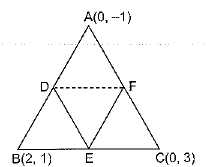
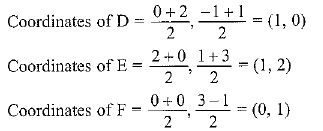
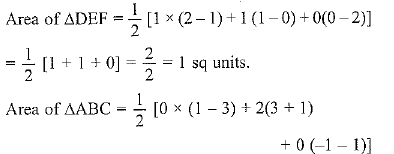
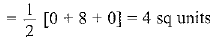
The ratio of ar ΔDEF and ar ΔABC is 1 : 4
Q.4. Find the area of the quadrilateral whose vertices, taken in order, are (−4, −2), (−3, −5), (3, −2) and (2, 3).
Sol. Area of ΔABC
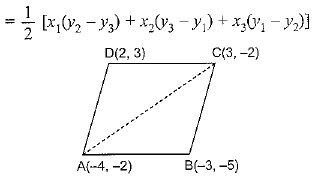
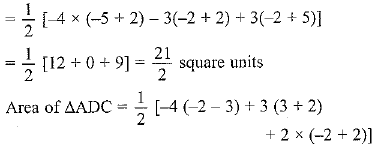
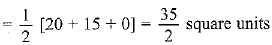
The area of quadrilateral ABCD
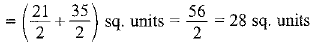
Q.5. You have studied in class IX (Chapter 9, Example 3) that, a median of a triangle divides it into two triangles of equal areas. Verify this result for ∆ ABC whose vertices are A (4, −6), B (3, −2) and C (5, 2).
Sol. D is the mid-point of BC, then coordinates of D are
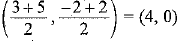
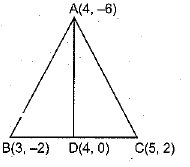
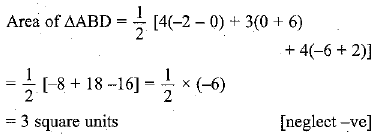
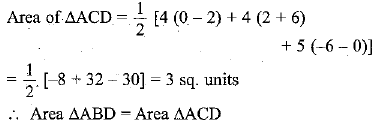
⇒ A median of a triangle divides it into two triangles of equal areas.