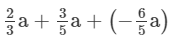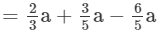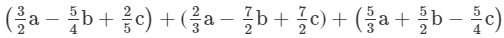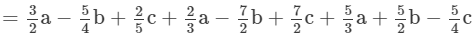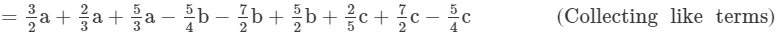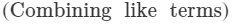RD Sharma Solutions for Class 8 Math Chapter 6 - Algebraic Expressions and Identities (Part-1) | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1: Identify the terms, their coefficients for each of the following expressions:
(i) 7x2yz − 5xy
(ii) x2 + x + 1
(iii) 3x2y2 − 5x2y2z2 + z2
(iv) 9 − ab + bc − ca
(v) a/2 + b/2 -ab
(vi) 0.2x − 0.3xy + 0.5y
Answer 1: Definitions:
A term in an algebraic expression can be a constant, a variable or a product of constants and variables separated by the signs of addition (+) or subtraction (−) . Examples: 27, x, xyz,1/2x2yz etc.
The number factor of the term is called its coefficient.
(i) The expression 7x2yz−5xy consists of two terms, i.e., 7x2yz and −5xy.
The coefficient of 7x2yz is 7 and the coefficient of −5xy is −5.
(ii) The expression x2+x+1 consists of three terms , i.e., x2, x and 1.
The coefficient of each term is 1.
(iii) The expression 3x2y2−5x2y2z2+z2 consists of three terms , i.e., 3x2y2, −5x2y2z2 and z2. The coefficient of 3x2y2 is 3. The coefficient of −5x2y2z2 is −5 and the coefficient of z2 is 1.
(iv) The expression 9−ab+bc−ca consists of four terms — 9,−ab, bc and −ca. The coefficient of the term 9 is 9. The coefficient of −ab is −1. The coefficient of bc is 1, and the coefficient of −ca is −1.
(v) The expression a/2 + b/2 -abconsists of three terms , i.e.,a/2, b/2 and −ab. The coefficient of a/2 is 1/2. The coefficient of b/2 is (vi) The expression 0.2x−0.3xy+0.5y consists of three terms , i.e., 0.2x, −0.3xy and 0.5y. The coefficient of 0.2x is 0.2. The coefficient of −0.3xy is −0.3, and the coefficient of 0.5y is 0.5. 1/2, and the coefficient of −ab is −1.
Question 2: Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any category?
(i) x + y
(ii) 1000
(iii) x + x2 + x3 + 4y4
(iv) 7 + a + 5b
(v) 2b − 3b2
(vi) 2y − 3y2 + 4y3
(vii) 5x − 4y + 3x
(viii) 4a − 15a2
(ix) xy + yz + zt + tx
(x) pqr
(xi) p2q + pq2
(xii) 2p + 2q
Answer 2: Definitions:
A polynomial is monomial if it has exactly one term. It is called binomial if it has exactly two non-zero terms. A polynomial is a trinomial if it has exactly three non-zero terms.
(i) The polynomial x+y has exactly two non zero terms , i.e., x and y. Therefore, it is a binomial.
(ii) The polynomial 1000 has exactly one term, i.e., 1000. Therefore, it is a monomial.
(iii) The polynomial x+x2+x3+x4 has exactly four terms, i.e., x, x2, x3 and x4. Therefore, it doesn't belong to any of the categories.
(iv) The polynomial 7+a+5b has exactly three terms, i.e., 7, a and 5b. Therefore, it is a trinomial.
(v) The polynomial 2b−3b2 has exactly two terms, i.e., 2b and −3b2. Therefore, it is a binomial.
(vi) The polynomial 2y−3y2+4y3 has exactly three terms, i.e., 2y, −3y2 and 4y3. Therefore, it is a trinomial.
(vii) The polynomial 5x−4y+3x has exactly three terms, i.e., 5x, −4y and 3x. Therefore, it is a trinomial.
(viii) The polynomial 4a−15a2 has exactly two terms, i.e., 4a and −15a2. Therefore, it is a binomial.
(ix) The polynomial xy+yz+zt+tx has exactly four terms xy, yz, zt and tx. Therefore, it doesn't belong to any of the categories.
(x) The polynomial pqr has exactly one term, i.e., pqr. Therefore, it is a monomial.
(xi) The polynomial p2q+pq2 has exactly two terms, i.e., p2q and pq2. Therefore, it is a binomial.
(xi) The polynomial 2p+2q has two terms, i.e., 2p and 2q. Therefore, it is a binomial.
Question 3: Add the following algebraic expressions:
(i) 3a2b, − 4a2b, 9a2b
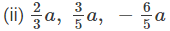
(iii) 4xy2 − 7x2y, 12x2y − 6xy2, − 3x2y +5xy2
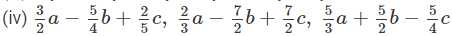

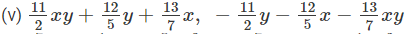
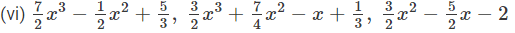
Answer 3:(i) To add the like terms, we proceed as follows:
3a2b+(−4a2b)+9a2b=3a2b−4a2b+9a2b=(3−4+9)a2b (Distributive law)=8a2b
(ii) To add the like terms, we proceed as follows:
=1/15 a
(iii) To add, we proceed as follows:
(4xy2−7x2y)+(12x2y)+(−6xy2)+(−3x2y+5xy2)=4xy2−7x2y+12x2y−6xy2−3x2y+5xy2=4xy2−6xy2+5xy2−7x2y+12x2y−3x2y ( Collecting like terms )=3xy2+2x2y
(iv) To add, we proceed as follows:
(v) To add, we proceed as follows:
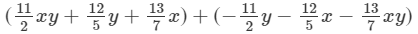
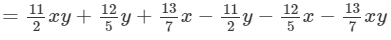
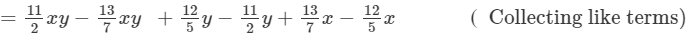
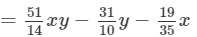
(vi) To add, we proceed as follows:
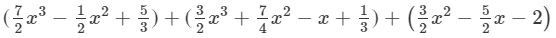
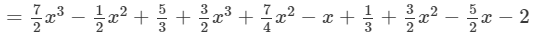
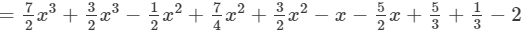 ( Combining like terms)
( Combining like terms)
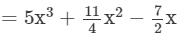 ( Combining like terms)
( Combining like terms)
Question 4: Subtract:
(i) − 5xy from 12xy
(ii) 2a2 from − 7a2
(iii) 2a − b from 3a − 5b
(iv) 2x3 − 4x2 + 3x + 5 from 4x3 + x2 + x + 6

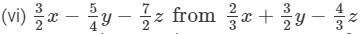
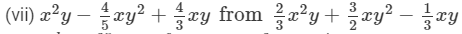
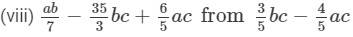
Answer 4: (i) 12xy−(−5xy)=12xy+5xy=17xy
(ii) −7a2−(2a2)=−7a2−2a2=−9a2
(iii) (3a−5b)−(2a−b)=(3a−5b)−2a+b=3a−5b−2a+b=3a−2a−5b+b=a−4b
(iv) (4x3+x2+x+6)−(2x3−4x2+3x+5)
=4x3+x2+x+6−2x3+4x2−3x−5
=4x3−2x3+x2+4x2+x−3x+6−5 (Collecting like terms)
=2x3+5x2−2x+1 (Combining like terms)
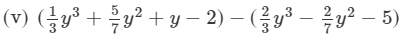
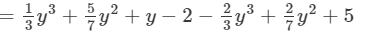
 (Combining like terms)
(Combining like terms)
=−1/3 y3+y2+y+3 (Combining like terms)
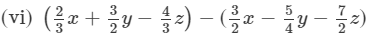
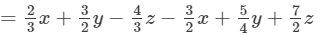
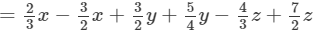 (Collecting like terms )
(Collecting like terms )
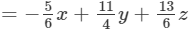 (Combining like terms)
(Combining like terms)
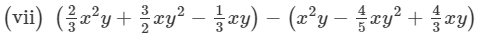
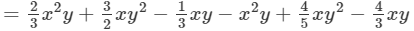
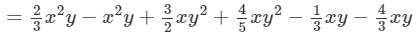 (Collecting like terms)
(Collecting like terms)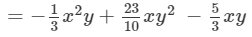 (Combining like terms)
(Combining like terms)
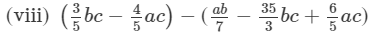
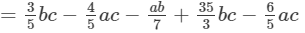
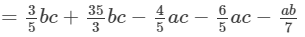 (Collecting like terms)
(Collecting like terms)
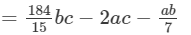 (Combining like terms)
(Combining like terms)
Question 5: Take away:
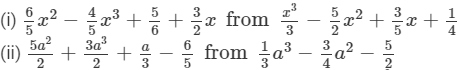
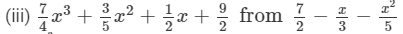
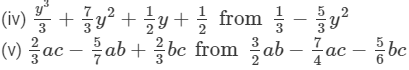
Answer 5:(i) The difference is given by:
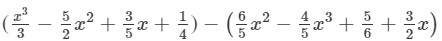
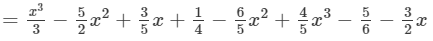
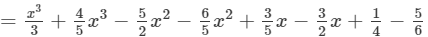 (Collecting like terms)
(Collecting like terms)
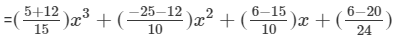
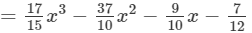 (Combining like terms)
(Combining like terms)
(ii) The difference is given by:
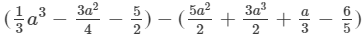
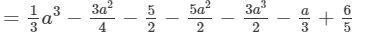
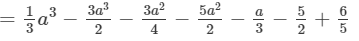 (Collecting like terms)
(Collecting like terms)
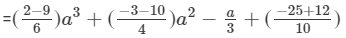
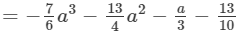 (Combining like terms)
(Combining like terms)
(iii) The difference is given by:
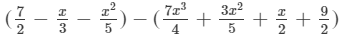
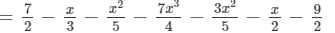
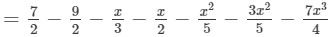 (Collecting like terms)
(Collecting like terms)
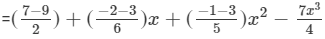
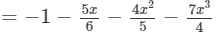 (Combining like terms )
(Combining like terms )
(iv) The difference is given by:
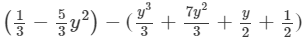
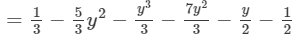
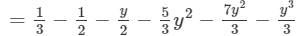 ( Collecting like terms)
( Collecting like terms)
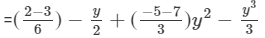
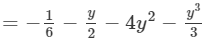 (Combining like terms. )
(Combining like terms. )
(v) The difference is given by:
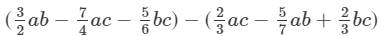
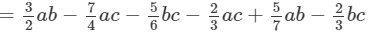
 (Collecting like terms )
(Collecting like terms )
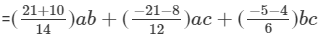
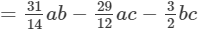 (Combining like terms )
(Combining like terms )
Question 6: Subtract 3x − 4y − 7z from the sum of x − 3y + 2z and − 4x + 9y − 11z.
Answer 6: Let first add the expressions x−3y+2z and −4x+9y−11z. We get:
(x−3y+2z)+(−4x+9y−11z)
=x−3y+2z−4x+9y−11z
=x−4x−3y+9y+2z−11z (Collecting like terms)
=−3x+6y−9z (Combining like terms)
Now, subtracting the expression 3x−4y−7z from the above sum; we get:
(−3x+6y−9z)−(3x−4y−7z)=−3x+6y−9z−3x+4y+7z
=−3x−3x+6y+4y−9z+7z (Collecting like terms)
=−6x+10y−2z (Combining like terms)
Thus, the answer is −6x+10y−2z.
Question 7: Subtract the sum of 3l − 4m − 7n2 and 2l + 3m − 4n2 from the sum of 9l + 2m − 3n2 and − 3l + m + 4n2 .....
Answer 7: We have to subtract the sum of (3l − 4m − 7n2) and (2l + 3m − 4n2) from the sum of (9l + 2m − 3n2) and (−3l + m + 4n2)
{(9l+2m−3n2)+(−3l+m+4n2)}−{(3l−4m−7n2)+(2l+3m−4n2)}
=(9l−3l+2m+m−3n2+4n2)−(3l+2l−4m+3m−7n2−4n2)
=(6l+3m+n2)−(5l−m−11n2) (Combining like terms inside the parentheses)
=6l+3m+n2−5l+m+11n2
=6l−5l+3m+m+n2+11n2 (Collecting like terms)
=l+4m+12n2 (Combining like terms)
Thus, the required solution is l+4m+12n2.
Question 8: Simplify each of the following:
(i) x2 − 3x + 5 − 12 (3x2 − 5x + 7)
(ii) [5 − 3x + 2y − (2x − y)] − (3x − 7y + 9)
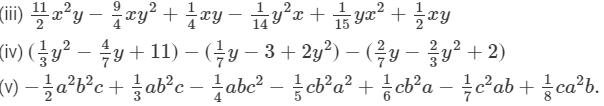
Answer 8: (i) x2−3x+5−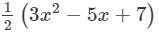
=x2−3x+5− 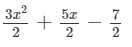

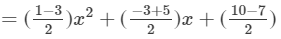
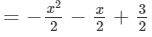
Thus, the answer is 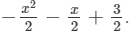
(ii) [5−3x+2y−(2x−y)]−(3x−7y+9)=[5−3x+2y−2x+y]−(3x−7y+9)=[5−5x+3y]−(3x−7y+9)=5−5x+3y−3x+7y−9=5−9−5x−3x+3y+7y=−4−8x+10y 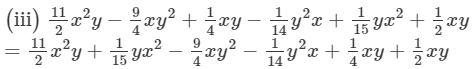 (Collecting like terms)
(Collecting like terms)
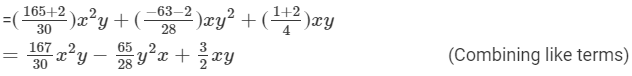
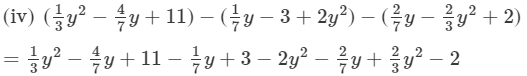
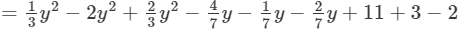 (Collecting like terms)
(Collecting like terms)
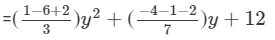
=−y2−7y+12 (Combining like terms)
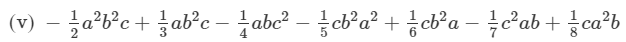
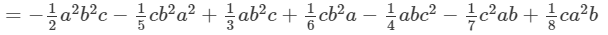 (Collecting like terms)
(Collecting like terms)
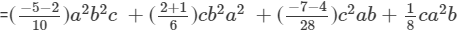
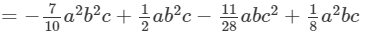 (Combining like terms)
(Combining like terms)
Question 6: Subtract the sum of 2x − x2 + 5 and − 4x − 3 + 7x2 from 5.
Answer 6: We have to subtract the sum of (2x − x2 + 5) and (− 4x − 3 + 7x) from 5.
5−{(2x−x2+5)+(−4x−3+7x2)}=5−(2x−4x−x2+7x2+5−3)=5−2x+4x+x2−7x2−5+3
=5−5+3−2x+4x+x2−7x2 (Collecting like terms)
=3+2x−6x2 (Combining like terms)
Thus, the answer is 3+2x−6x2.
FAQs on RD Sharma Solutions for Class 8 Math Chapter 6 - Algebraic Expressions and Identities (Part-1) - RD Sharma Solutions for Class 8 Mathematics
| 1. What are algebraic expressions? |  |
| 2. How do you simplify algebraic expressions? |  |
| 3. What are identities in algebraic expressions? |  |
| 4. How do you expand algebraic expressions? |  |
| 5. What is the difference between an algebraic expression and an equation? |  |