Fractions Class 6 Notes Maths Chapter 7
Introduction
A fraction is a way to represent a part of a whole.
The whole can be a single object or a group of objects.
- Imagine you have one whole pizza. If you cut it into two equal slices, each slice is called one-half, written as .

- If you divide the pizza into four equal slices, each slice is one-fourth, written as .

- If you eat three out of those four slices, you have eaten three-fourths of the pizza, written as .

- Similarly, If you have a chocolate bar and break it into 8 equal pieces, each piece is of the chocolate bar. If you eat 3 pieces, you’ve eaten of the bar.
Let us understand this concept better.
A Fraction
A fraction means a part of a group or of a region.

When we look at a fraction, it has two important numbers:
Numerator (Top Number):
- This tells us how many parts of the whole we have or are using.
- For example, in the fraction
 , the numerator is 5, meaning we have 5 parts out of the total.
, the numerator is 5, meaning we have 5 parts out of the total.
Denominator (Bottom Number):
- This tells us into how many equal parts the whole is divided.
- In
 , the denominator is 12, meaning the whole is divided into 12 equal parts.
, the denominator is 12, meaning the whole is divided into 12 equal parts.

Let us understand fractions with the help of an example:
Ethan is celebrating his birthday at home. His mother has baked a cake for his birthday. When his friends came home, he cut the cake.
His mother wants to distribute the cake equally among all his friends.
There are six people (including Ethan’s mother) at the party.
So, his mother cuts the cake into 6 equal parts.
 Fractions of a Cake
Fractions of a Cake
Can you tell what fraction of the cake Ethan gets?
Total number of slices of cake = 6
Ethan got (one-sixth) part of the cake.
So, Ethan ate one part out of six parts of the cake.
Here 1 is the numerator and 6 is the denominator.

Fraction on the Number Line
Representing fractions on a number line means that we can plot fractions on a number line, which is similar to plotting whole numbers and integers. Fractions represent parts of a whole.So, fractions on the number line are represented by making equal parts of a whole i.e. 0 to 1, and the number of those equal parts would be the same as the number written in the denominator of the fraction. For example, to represent 1/8 on the number line, we have to divide 0 to 1 into 8 equal parts and mark the first part as 1/8.
1. Understand the Number Line Basics:
- A number line is a straight line where numbers are placed at equal distances.
- Whole numbers like 0, 1, 2, etc., are marked on this line.
2. Identify the Fraction to Show:
- For example, you want to show the fraction 3/7.
- This fraction means you have 3 parts out of 7 equal parts.
3. Divide the Length Between 0 and 1:
- Since the denominator is 7, divide the length between 0 and 1 into 7 equal parts.
4. Mark the Fraction:
- Count 3 parts from 0. The point where you stop is 3/7 on the number line.
- Mark this point as "P" to show 3/7.

5. Mark Other Related Fractions:
- /7: This is simply 0, so mark it at the starting point of the line.
- /7: Since is equal to 1, mark it at the point where 1 is on the number line.
Examples:
- Consider a fraction 1/2.
1/2 is greater than 0, but less than 1.
Divide the space between 0 and 1 into two equal parts. We can show one part as the fraction 1/2
- Consider another 1/5.
1/5 fraction is greater than 0, but less than 1.
Divide the space between 0 and 1 into five equal parts. We can show the first part as 1/5 the second as 2/5 the third as 3/5 the fourth as 4/5 and the fifth part as 5/5=1.
Types of Fractions
Let us understand the different types of fractions. There are three types of fractions. They are:
1. Proper fractions
2. Improper fractions
3. Mixed fractions

Proper Fractions
- A proper fraction is a type of fraction where the numerator (the top number) is smaller than the denominator (the bottom number).

- This means the fraction represents a part of a whole that is less than 1. In a proper fraction, the number in the denominator shows the number of parts into which the whole is divided, while the number in the numerator shows the number of parts that have been taken.
- Here, the numerator is always less than the denominator such fractions are termed as a proper fraction.

When you locate proper fractions like 1/6, 2/6, 4/6 on a number line, you'll notice a few things:
- All these fractions will be located to the left of 1 because they are less than 1.
- None of these fractions lie beyond 1 because proper fractions are always less than 1. Fractions greater than 1 are called improper fractions, where the numerator is greater than or equal to the denominator.
Example 1: Give the proper fraction whose denominator is 9 and numerator is 5.
Ans: Given numerator is 5 and denominator is 9
We know that Fraction = Part/ Whole
So, Fraction = 5/9
Hence, required fraction is 5/9
Example 2: Fill in the blank using ‘>’, ‘<’, or ‘=’:
Ans: 
 is half of 1, so it's less than 1.
is half of 1, so it's less than 1.
Improper and Mixed Fractions
Improper Fractions
- A fraction where the numerator (the top number) is larger than the denominator (the bottom number). This means the fraction represents a quantity greater than or equal to 1.

- 9/5 is an improper fraction as it means 9 parts are being divided into groups of 5. It means you have 9 parts, and each part is one-fifth of a whole. Since 9 is more than 5, this fraction is greater than 1.
- To understand 9/5, you can think of it as dividing 9 by 5. When you do this division, the result is 1 whole (5/5) with 4 parts remaining.
So, 9/5 can be written as: 1 (whole) + 4/ 5 (parts left over)
Mixed Fractions
- A mixed fraction combines a whole number with a proper fraction. It shows how many whole parts there are, along with a fraction of another part.

- Example:
 means you have 1 whole and an additional 4/5 of another whole.
means you have 1 whole and an additional 4/5 of another whole.
Conversion of Improper fraction into Mixed fraction and Vice Versa
1. Conversion of improper fraction into mixed fraction
An improper fraction can be expressed as mixed fraction by dividing the numerator by the denominator of the improper fraction to obtain the quotient and the remainder.
Divide the Numerator by the Denominator:
- The numerator is the number on top, and the denominator is the number on the bottom of the fraction.
- Perform the division to get a quotient (the whole number part) and a remainder (the part left over).
Form the Mixed Fraction:
The quotient becomes the whole number part of the mixed fraction.
The remainder becomes the new numerator of the fraction, and the denominator remains the same.
The mixed fraction is then written as:
Then the mixed fraction will be.

Example: Improper fraction to Mixed Fraction 2. Conversion of mixed fraction into improper fraction:
Improper fraction to Mixed Fraction 2. Conversion of mixed fraction into improper fraction:
Multiply the Whole Number by the Denominator:
- Start by taking the whole number part of the mixed fraction and multiplying it by the denominator (the bottom number of the fraction).
Add the Numerator to the Product:
- After multiplying, add the numerator (the top number of the fraction) to the product from the first step.
Form the Improper Fraction:
- The sum from step 2 becomes the numerator of the improper fraction.
The denominator remains the same as in the original fraction.
Let us convert this mixed fraction to an improper fraction using the following steps and the explanation given below.
- Step 1: Multiply the denominator of the mixed fraction with the whole number part. In this case, 5 × 2 = 10
- Step 2: Add the numerator to the product obtained from Step 1. Here, 4 + 10 = 14.
- Step 3: Write the improper fraction with the sum obtained from Step 2 in the numerator/denominator form. Here, it will be 14/5.
 Mixed Fraction to Improper Fraction
Mixed Fraction to Improper Fraction
Equivalent Fractions
These are fractions that represent the same value or part of a whole, even though they have different numerators and denominators.
 Equivalent Fractions
Equivalent Fractions
How to Find Equivalent Fractions
Multiplying Both Numerator and Denominator: To find an equivalent fraction, multiply both the numerator (top number) and the denominator (bottom number) by the same number.

Dividing Both Numerator and Denominator: Alternatively, you can divide both the numerator and the denominator by the same number to find equivalent fractions.

Equivalent fractions represent the same part of a whole because they are different ways of expressing the same proportion. When you multiply or divide the numerator and denominator by the same number, you are essentially scaling the fraction but keeping the same overall value.
Example 1: Find any 3 equivalent fractions of  .
.
Ans:
- If we multiply both the numerator and denominator with the same non zero number, we will get its equivalent fraction.If we multiply given fraction by:
 =
=  =
= 
 =
=  =
= 
 =
=  =
= 
Example 2: Are 1/3 and 4/7 equivalent?
Ans: No, because they do not represent the same part of a whole.
Simplest Form of a Fraction
A fraction is said to be in the simplest (or lowest) form if its numerator and denominator have no common factor except 1.
This means that the fraction cannot be reduced any further. 
How to Simplify a Fraction to Its Lowest Form
Find the Highest Common Factor (HCF):
- The HCF, also known as the Greatest Common Divisor (GCD), is the largest number that divides both the numerator and the denominator exactly.
Divide the Numerator and Denominator by the HCF:
- Once you find the HCF, divide both the numerator (top number) and the denominator (bottom number) by this number.
Write the Resulting Fraction:
- The fraction you get after dividing by the HCF is the simplest form of the original fraction.
Example 1: Find the simplest form of the fraction 11/33
Example 2: Convert 350/175 into simplest form
Ans: The HCF of 350 and 175 is 175.
So, Divide both the numerator and the denominator by their 175:

So, the simplest form of 350/175 is /1, which is equal to 2.
Like Fractions
Like fractions and unlike fractions refer to the relationships between the denominators of two or more fractions.
 Like and Unlike Fractions
Like and Unlike Fractions
1. Like Fractions
- Like fractions have the same denominator.
- Example: 3/4 and 2/4 are like fractions because they share the common denominator 4.
2. Unlike Fractions
- Unlike fractions have different denominators.
- Example: 2/5 and 3/8 are unlike fractions because they have different denominators (5 and 8).
Comparing Fractions
1. Comparing Like Fractions
If the fractions have the same denominator (bottom number), you can compare them directly by looking at the numerators (top numbers).
In like fractions, the fraction with the greater numerator is greater.
 Comparing Like Fractions
Comparing Like Fractions
Example 1: Among fractions 5/7 and 3/7, 5/7 is greater than 3/7 as 5 is greater than 3.
Example 2: Compare: 5/12 and 17/12.
- Step 1: First, observe the denominators of the given fractions, i.e., 5/12 and 17/12. Here, the denominators are the same for both fractions.
- Step 2: Now, compare the numerators of the given fractions. We can observe that 17 > 5.
- Step 3: We know that the fraction with the larger numerator is larger. Hence, 5/12 < 17/12.
2. Comparing Unlike Fractions
- If two fractions with the same numerator but different denominators are to be compared, then the fraction with the smaller denominator is the greater of the two.
- To compare fractions with unlike denominators, we have to convert them to like denominators for which we have to find the Least Common Multiple (LCM) of the denominators. As the denominators are made equal, we can compare the fractions with ease.
 Comparing Unlike Fractions
Comparing Unlike Fractions
Example: Compare: 1/4 and 2/3.
Step 1: First, observe the denominators of the given fractions, i.e., 1/4 and 2/3. Since the denominators are different make them equal by finding the LCM of 4 and 3. LCM(4,3) = 12.
Step 2: Now, let us convert the given fraction in such a way that they have the same denominators. So, multiply the first fraction with 3/3, i.e., 1/4 × 3/3 = 3/12.
Step 3: Similarly, multiply the second fraction with 4/4, i.e., 2/3 × 4/4 = 8/12. Thus, the first fraction becomes 3/12 and the other becomes 8/12.
Step 4: Compare the obtained new fractions, i.e., 3/12 and 8/12. As the denominators are the same, we will compare the numerators. We can observe that 3 < 8.
Step 5: The fraction that has a large numerator is the larger fraction. So, 8/12 > 3/12. So, 2/3 > 1/4.
Addition and Subtraction of Fractions
Addition and subtraction of fractions involve combining or taking away portions of quantities represented by the fractions. Here's a brief overview:

1. Addition and Subtraction of two like fractions
When we add or subtract like fractions, we add or subtract their numerators and the denominator remains the same.
1)  +
+ 
The two fractions are like fractions, so we add their numerators and keep the denominator the same. +
+  =
=  =
= 
2)  −
− 
Here, the given fractions are like fractions. So, we subtract their numerators and keep the denominator the same.
 −
−  =
=  =
= 
2. Addition and Subtraction of two unlike fractions
When we add or subtract unlike fractions we follow the following steps:
1)  +
+ 
The given fractions are unlike fractions, so we first find LCM of their denominators.
LCM of 8 and 24 = 2 × 2 × 2 × 3 = 24
Now, we convert the fractions into like fractions.
(Changing the denominator of fractions to 24)
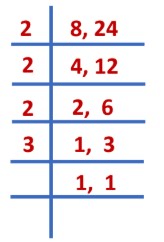
 =
=  and
and
 +
+  = =
= = 
2)  -
- 
As the given fractions are unlike fractions, we find the LCM of their denominator.
LCM of 15 and 27 = 3 × 3 × 3 × 5 = 135
Next, we convert the fractions into like fractions
(Fractions with the same denominator)

 =
=  and
and  =
= 
 -
-  =
=  =
= 
3. Addition and Subtraction of Mixed Fractions
Before applying any operations such as addition, subtraction, multiplication, etc., change the given mixed fractions to improper fractions.
After converting the mixed fractions to improper fractions, one can proceed with the calculations, which are as follows:
Method 1: Separate Whole Numbers and Fractions
Add/Subtract Whole Numbers: Perform the addition or subtraction with the whole numbers separately.
Add/Subtract Fractions: Make sure the fractions have a common denominator before adding or subtracting.
Combine the Results: Add or subtract the results of the whole numbers and fractions to get the final answer.
Example 1: 
Ans:


Example 2:
Ans:

Method 2: Convert Mixed Fractions to Improper Fractions
Convert Mixed Fractions to Improper Fractions: Multiply the whole number by the denominator of the fraction and add the numerator.
Perform Addition/Subtraction: Use the common denominator to add or subtract the improper fractions.
Convert Back to Mixed Fraction: If needed, convert the resulting improper fraction back to a mixed fraction.
Example 1: 
Ans: Convert to Improper Fractions:

Find a Common Denominator:


Example 2: 
Ans: 

Important Questions for Exam
Q1: A rectangular sheet of paper 12  is cm long and 9
is cm long and 9  cm wide. Find its perimeter.
cm wide. Find its perimeter.
Length of the rectangular sheet = 12
cm. 12
=
=
=

Breadth of the rectangular sheet = 9
cm
Perimeter of a rectangle = 2(l + b)
Perimeter of rectangular sheet of paper
= 2 (+
) = 2(
) = 2 (
)
= 44 cm
Q2: Michael finished coloring a picture in  hour. Vaibhav finished colouring the same picture in
hour. Vaibhav finished colouring the same picture in  hour. Who worked longer? By what fraction was it longer?
hour. Who worked longer? By what fraction was it longer?
Time taken by Michael to colour the picture =
hour
Time taken by Vaibhav to colour the same picture =
hour
The two fractions are unlike, so we first convert them to like fractions (fractions having the same denominator).
'
LCM of 12 and 4 = 2 × 2 × 3 = 12
and
=
On comparing the two fractions we get,
>
Therefore, Vaibhav worked longer by
-
=
=
=
hour.
Q3: Compare the fractions 4/25 and 33/100.
To compare the given fractions, find their decimal values. So, divide 4 by 25 and 33 by 100.
4/25 = 0.16
33/100 = 0.33
From the decimal values, we can conclude that 0.33 > 0.16. So, 33/100 is greater than 4/25.
Therefore, 33/100 is greater than 4/25.
Q4: Mrunal was asked to prove that the given fractions are equal: 30/90 and 25/75. Can you prove the given statement using the LCM method?
Given fractions: 30/90 and 25/75.
The denominators of the given fractions are different. So, find out the LCM of the denominators, i.e., LCM(90, 75) = 450.
Now, multiply 30/90 with 5/5 and 25/75 with 6/6.
30/90 × 5/5 = 150/450
25/75 × 6/6 = 150/450
Compare the numerators now, as the denominators are the same.
So, 150 = 150, i.e., 150/450 = 150/450.
Thus, 30/90 = 25/75, i.e., both the given fractions are equal.
Hence, proved.
Q5: Which of the following fractions is larger: 27/41 or 27/67?
Given fractions: 27/41 and 27/67.
Here, the numerators of both fractions are the same but the denominators are different.
We know that the fraction that has a smaller denominator has a greater value, while the fraction that has a larger denominator has a smaller value.
Here, 41 < 67.
So, 27/41 > 27/67
Therefore, 27/41 is the larger fraction.
|
92 videos|348 docs|54 tests
|
FAQs on Fractions Class 6 Notes Maths Chapter 7
| 1. What is a fraction and how is it represented? |  |
| 2. How can we locate a fraction on a number line? |  |
| 3. What are proper fractions, and how do they differ from improper fractions? |  |
| 4. How do we find equivalent fractions? |  |
| 5. How can we add or subtract fractions with different denominators? |  |





 , the numerator is 5, meaning we have 5 parts out of the total.
, the numerator is 5, meaning we have 5 parts out of the total. , the denominator is 12, meaning the whole is divided into 12 equal parts.
, the denominator is 12, meaning the whole is divided into 12 equal parts.




 means you have 1 whole and an additional 4/5 of another whole.
means you have 1 whole and an additional 4/5 of another whole.
 =
= 

 =
= 

 =
= 
 cm. 12
cm. 12  =
=  =
=  =
= 
 Breadth of the rectangular sheet = 9
Breadth of the rectangular sheet = 9  cm
cm Perimeter of a rectangle = 2(l + b)
Perimeter of a rectangle = 2(l + b) +
+ ) = 2(
) = 2( ) = 2 (
) = 2 ( )
)
 hour
hour hour
hour
 '
'  LCM of 12 and 4 = 2 × 2 × 3 = 12
LCM of 12 and 4 = 2 × 2 × 3 = 12 and
and  =
= 
 >
> 
 -
-  =
=  =
=  =
=  hour.
hour.

















