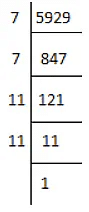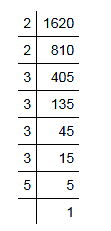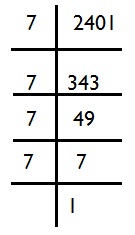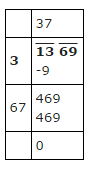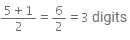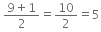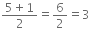NCERT Solutions for Class 8 Maths - Squares and Square Roots- 2
Exercise 6.3
Q.1. What could be the possible ‘one’s’ digits of the square root of each of the following numbers?
(i) 9801 (ii) 99856 (iii) 998001 (iv) 657666025
The possible digit at one’s place of the square root of:
(i) 9801 can be 1 or 9.
[∵ 1 *1 = 1 and 9 * 9 = 81]
(ii) 99856 can be 4 or 6.
[∵ 4 * 4 = 16 and 6 * 6 = 36]
(iii) 998001 can be 1 or 9.
[∵ 1 *1 = 1 and 9 * 9 = 81]
(iv) 657666025 can be 5.
[∵ 5 * 5 = 25]
Q.2.Without doing any calculation, find the numbers which are surely not perfect squares.
(i) 152 (ii) 257 (iii) 408 (iv) 441
We know that natural numbers ending with the digits 0, 2, 3, 7 and 8 are not perfect square.
i) 153⟹ Ends with 3.
Therefore, 153 is not a perfect square
ii) 257⟹ Ends with 7
Therefore, 257 is not a perfect square
iii) 408⟹ Ends with 8
Therefore, 408 is not a perfect square
iv) 441⟹ Ends with 1
Therefore, 441 is a perfect square.
Q.3. Find the square roots of 100 and 169 by the method of repeated subtraction.
(i)
We have⇒100 – 1 = 99 99 – 3 = 96 96 – 5 = 91
⇒91 – 7 = 84 84 – 9 = 75 75 – 11 = 64
⇒64 – 13 = 51 51 – 15 = 36 36 – 17 = 19
⇒19 – 19 = 0∵ We reach 0 by successive subtraction of 10 odd numbers.
∴
= 10.
(ii)
We have
⇒169 – 1 = 168 168 – 3 = 165 165 – 5 = 160
⇒160 – 7 = 153 153 – 9 = 144 144 – 11 = 133
⇒133 – 13 = 120 120 – 15 = 105 105 – 17 = 88
⇒88 – 19 = 69 69 – 21 = 48 48 – 23 = 25
⇒25 – 25 = 0∵ We reach 0 by successive subtraction of 13 odd numbers.
∴
= 13.
Q.4. Find the square roots of the following numbers by the Prime Factorisation Method.
(i) 729 (ii) 400 (iii) 1764 (iv) 4096 (v) 7744
(vi) 9604 (vii) 5929 (viii) 9216 (ix) 529 (x) 8100
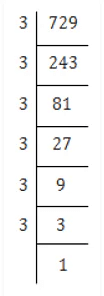
(i) We have
729 = 3×3×3×3×3×3×1
⇒ 729 = (3×3)×(3×3)×(3×3)
⇒ 729 = (3×3×3)×(3×3×3)
⇒ 729 = (3×3×3)2
⇒ √729 = 3×3×3 = 27
Thus, the square root of 729 is 27.
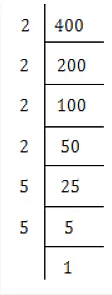
(ii) We have
400 = 2×2×2×2×5×5×1
⇒ 400 = (2×2)×(2×2)×(5×5)
⇒ 400 = (2×2×5)×(2×2×5)
⇒ 400 = (2×2×5)2
⇒ √400 = 2×2×5 = 20
Thus, the square root of 400 is 20.
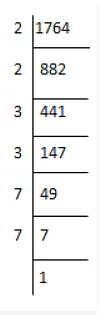
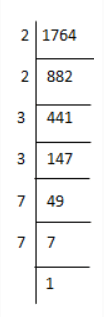
(iii) We have
1764 = 2×2×3×3×7×7
⇒ 1764 = (2×2)×(3×3)×(7×7)
⇒ 1764 = (2×3×7)×(2×3×7)
⇒ 1764 = (2×3×7)2
⇒ √1764 = 2 ×3×7 = 42
Thus, The square root of 1764 is 42.
(iv) We have
4096 = 2×2×2×2×2×2×2×2×2×2×2×2
⇒ 4096 = (2×2)×(2×2)×(2×2)×(2×2)×(2×2)×(2×2)
⇒ 4096 = (2×2×2×2×2×2)×(2×2×2×2×2×2)
⇒ 4096 = (2×2×2×2×2×2)2
⇒ √4096 = 2×2×2 ×2×2×2 = 64
Thus, the square root of 4096 is 64.
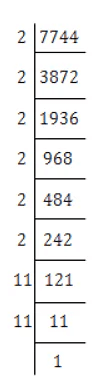
(v) We have
7744 = 2×2×2×2×2×2×11×11×1
⇒ 7744 = (2×2)×(2×2)×(2×2)×(11×11)
⇒ 7744 = (2×2×2×11)×(2×2×2×11)
⇒ 7744 = (2×2×2×11)2
⇒ √7744 = 2×2×2×11 = 88
Thus, the square root of 7744 is 88.
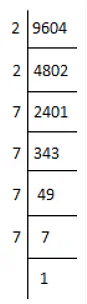
(vi) We have
9604 = 62 × 2 × 7 × 7 × 7 × 7
⇒ 9604 = ( 2 × 2 ) × ( 7 × 7 ) × ( 7 × 7 )
⇒ 9604 = ( 2 × 7 ×7 ) × ( 2 × 7 ×7 )
⇒ 9604 = ( 2×7×7 )2
⇒ √9604 = 2×7×7 = 98
Thus, the square root of 9604 is 98.
(vii) We have
5929 = 7×7×11×11
⇒ 5929 = (7×7)×(11×11)
⇒ 5929 = (7×11)×(7×11)
⇒ 5929 = (7×11)2
⇒ √5929 = 7×11 = 77
Thus, the square root of 5929 is 77.
(viii) We have
9216 = 2×2×2×2×2×2×2×2×2×2×3×3×1
⇒ 9216 = (2×2)×(2×2) × ( 2 × 2 ) × ( 2 × 2 ) × ( 2 × 2 ) × ( 3 × 3 )
⇒ 9216 = ( 2 × 2 × 2 × 2 × 2 × 3) × ( 2 × 2 × 2 × 2 × 2 × 3)
⇒ 9216 = 96 × 96
⇒ 9216 = ( 96 )2
⇒ √9216 = 96Thus, The square root of 9216 is 96.
(ix) We have:
⇒ 529 = 23×23
⇒ 529 = (23)2
⇒ √529 = 23Thus, the square root of 529 is 23
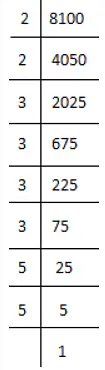
(x) We have
8100 = 2×2×3×3×3×3×5×5×1
⇒ 8100 = (2×2) ×(3×3)×(3×3)×(5×5)
⇒ 8100 = (2×3×3×5)×(2×3×3×5)
⇒ 8100 = 90×90
⇒ 8100 = (90)2
⇒ √8100 = 90
Thus, the square root of 8100 is 90.
Question 5. For each of the following numbers, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also, find the square root of the square number so obtained.
(i) 252 (ii) 180 (iii) 1008 (iv) 2028 (v) 1458 (vi) 768
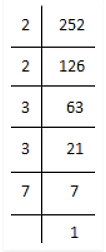
(i) We have
252 = 2×2×3×3×7
= (2×2)×(3×3)×7
Here, 7 cannot be paired.
∴ We will multiply 252 by 7 to get perfect square.
New number = 252 × 7 = 1764
1764 = 2×2×3×3×7×7
⇒ 1764 = (2×2)×(3×3)×(7×7)
⇒ 1764 = 22×32×72
⇒ 1764 = (2×3×7)2
⇒ √1764 = 2×3×7 = 42
(ii) We have
180 = 2 * 2 * 3 * 3 * 5
Here, the prime factor 5 has no pair.
∴ We will multiply 180 by 5 to make a perfect square
∴ [180] * 5 = [2 * 2 * 3 * 3 * 5] * 5
or 900 = 2 * 2 * 3 * 3 * 5 * 5
or
= 2 * 3 * 5 = 30
Thus, the required smallest whole number = 5
Also, the square root of 900 is 30.
(iii) We have
1008 = 2 * 2 * 2 * 2 * 3 * 3 * 7
Here, the prime factor 7 has no pair.
∴ We multiply 1008 by 7 to make a perfect square.
∴ [1008] * 7 = [2 * 2 * 2 * 2 * 3 * 3 * 7] * 7
or 7056 = 2 * 2 * 2 * 2 * 3 * 3 * 7 * 7
or
= 2 * 2 * 3 * 7 = 84
Thus, the required smallest whole number = 7
Also the square root of 7056 is 84.
(iv) We have
2028 = 2 * 2 * 3 * 13 * 13
Here, the prime factor 3 has no pair.
∴We multiply 2028 by 3 to make a perfect square.
∴[2028] * 3 = [2 * 2 * 3 * 13 * 13] * 3
or 6084 = 2 * 2 * 3 * 3 * 13 * 13
or
= 2 * 3 * 13 = 78
Thus, the smallest whole number = 3 and
= 78
(v) We have
1458 = 2 * 3 * 3 * 3 * 3 * 3 * 3
Here, 2 has no pair.
∴ We multiply 1458 by 2 to make a perfect square.
∴ [1458] * 2 = [2 * 3 * 3 * 3 * 3 * 3 * 3] * 2
or 2916 = 2 * 2 * 3 * 3 * 3 * 3 * 3 * 3
or
= 2 * 3 * 3 * 3 = 54
Thus, the required smallest whole number = 2, and
= 54
(vi) We have
768 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 3
Here, Prime factor 3 has no pair.
∴ We multiply 768 by 3 to make a perfect square.
∴ [768] * 3 = [2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 3] * 3
2304 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3
or
= 2 * 2 * 2 * 2 * 3 = 48
Thus, the smallest whole number = 3 and
= 48.
Q.6. For each of the following numbers, find the smallest whole number by which it should be divided so as to get a perfect square. Also, find the square root of the square number so obtained.
(i) 252 (ii) 2925 (iii) 396 (iv) 2645 (v) 2800 (vi) 1620
(i) 252
We have
252 = 2 * 2 * 3 * 3 * 7
∵ The prime factor 7 is unpaired, so the given number should be divided by 7.
Thus, 36 is a perfect square. and
= 2 * 3 = 6
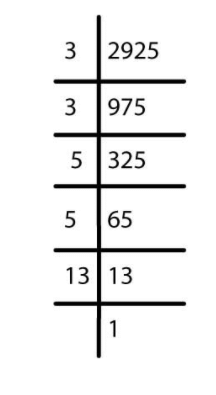
(ii) 2925
We have
2925 = 3 * 3 * 5 * 5 * 13
∵ The prime factor 13 is unpaired, so the given number should be divided by 13.
Thus, 225 is a perfect square. and
= 3 * 5 = 15
(iii) 396
We have
396 = 2 * 2 * 3 * 3 * 11
As the prime factor 11 is unpaired.
∴ Dividing the given number by 11,
∴ 36 is a perfect square. and,
= 2 * 3 = 6
(iv) 2645
We have
2645 = 5 * 23 * 23
∵ The prime factor 5 is unpaired.
∴ Dividing the given number by 5, we have
Thus, 529 is a perfect square and
= 23.
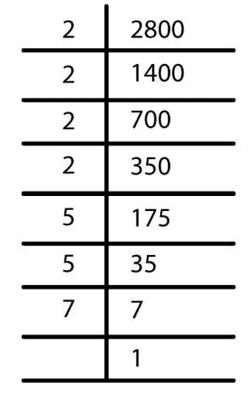
(v) 2800
We have
2800 = 2 * 2 * 2 * 2 * 5 * 5 * 7
Since 7 is unpaired.
∴ The given number should be divided by 7.
which is a perfect square.
∴= 2 * 2 * 5 = 20
(vi) 1620
We have
1620 = 2 * 2 * 3 * 3 * 3 * 3 * 5
∵ The prime factor 5 is unpaired.
∴ Dividing the given number by 5, we have
Q.7. The students of Class VIII of a school donated Rs 2401 in all, for Prime Minister’s National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
Let the number of students = x
∴ Each student donated Rs x.
Total amount donated by the class = Rs x * x = Rs x2
Thus, x2 = 2401
or
= 7 * 7 = 49
∴ The number of students in the class = 49.
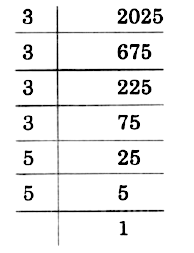
Q.8. 2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
Let the number of rows =x
∴ The number of plants is a row = x
So, the number of plants to be planted = x * x = x2
x2 = 2025
Thus, the required number of rows = 45
Also, the number of plants in a row = 45.
Q.9. Find the smallest square number that is divisible by each of the numbers 4, 9, and 10.
We know that LCM is the smallest number divisible by all its factors.
Since, LCM of 4, 9 and 10 = 2 * 2 * 9 * 5 = 180
But 180 is not a perfect square.
Again,
180 = 2 * 2 * 3 * 3 * 5 [∵ 9 = 3 * 3]
∵ It has 5 as unpaired.
∴ [180] * 5 = [2 * 2 * 3 * 3 * 5] * 5
or 900 = 2 * 2 * 3 * 3 * 5 * 5
∵ All the prime factors of 900 are paired.
∴ 900 is a perfect square.
Thus, the required number = 900.
Q.10. Find the smallest square number that is divisible by each of the numbers 8, 15 and 20
The smallest number divisible by 8, 15, and 20 is their LCM.
We have LCM = 2 * 2 * 5 * 2 * 3 = 120
But 120 is not a square number.
Now, to make it a perfect square, we have
120 = 2 * 2 * 2 * 3 * 5
or [120] * 2 * 3 * 5 = [2 * 2 * 2 * 3 * 5] * 2 * 3 * 5
or 3600 = 2 * 2 * 2 * 2 * 3 * 3 * 5 * 5
All factors of 3600 are paired. Therefore, 3600 is a perfect square.
∴ The required number = 3600.
Finding square root by division method
- For larger numbers, we use the division method for finding their square roots. This requires the pre-estimation of a number of digits in the square root.
- We know that the smallest 3-digit perfect square number is 100, which is the square of 10 (2-digit number).
- The greatest 3-digit perfect number is 961, which is the square of 31 (2-digit number).
- The greatest 4-digit perfect number is 9801, which is the square of 99 (2-digit number).
- We can say that “if a perfect square is a 3-digit or 4-digit number, then its square root will have 2-digits.”
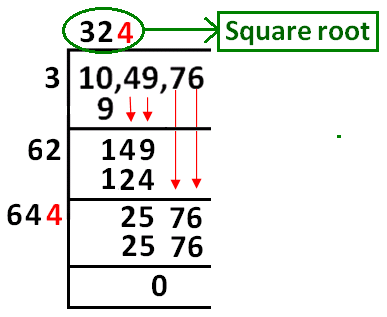 Division Method
Division Method
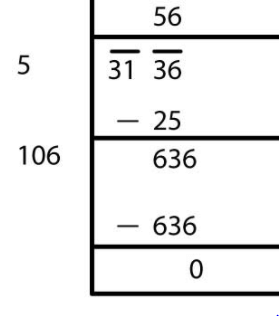
Example: Find the square root of 1369.
√1369 = 37
Think, Discuss, Write
Q.1. Can we say that if a perfect square is of n-digits, then its square root will have n/2 digits if n is even or (n+1)/2 if n is odd?
Yes, it is true.
Examples:
(i) 529 (a perfect number), n = 3 (odd number)
∴ Number of digits in square root = n+1/2
= 3+1/2 = 2
Also, √529 = 23 (2-digits).
(ii) 1296 (is perfect square) and n = 4 (even number)
∴ Number of digits of its square root = n/2 = 4/2 =2
Now √1296 = 36 (2-digits).
Q.2. Without calculating square roots, find the number of digits in the square root of the following numbers.
(i) 25600
(ii) 100000000
(iii) 36864
(i) 25600
∵ n = 5 [an odd number]
∴ Its square root will have (n+1)/2 digits,
i.e,
(ii) 100000000
∵ n = 9 → odd number
∴ Number of digits of its square root = n+1/2
=
(iii) 36864
∵ n = 5 → odd number
∴ Number of digits in its square root = n+1/2
Q.3. Estimate the value of the following to the nearest whole number.
(i) √80
(ii) √1000
(iii) √350
(iv) √500
(i) √80
∵ 102 = 100, 92 = 81, 82 = 64
and 80 is between 64 and 81.
i.e. 64 < 80 < 81
or 82 < 80 < 92
or 8 < √80 < 9
Thus, √80 lies between 8 and 9.
(ii) √1000
We know that
302 = 900, 312 = 961, 322 = 1024
∴ 1000 lies between 961 and 1024.
i.e. 916 < 1000 < 1024
or 312 < 1000 < 322
or 31 < √1000 < 32
Thus,√1000 lies between 31 and 32.
(iii) √350
We have 182 = 324, 192 = 361
Since, 350 lies between 324 and 316.
or 324 < 350 < 361
or 182 < 350 < 192
or 18 < √350 < 19
Thus, √350 lies between 18 and 19.
(iv) √500
∵ 222 = 484 and 232 = 529
Since, 500 lies between 484 and 529.
or 484 < 500 < 529
or 222 < 500 < 232
or 22 < √500 < 23
∴ √500 lies between 22 and 23.
Exercise 6.4
Q.1. Find the square root of each of the following numbers by the Division method.
(i) 2304
(ii) 4489
(iii) 3481
(iv) 529
(v) 3249
(vi) 1369
(vii) 5776
(viii) 7921
(ix) 576
(x) 1024
(xi) 3136
(xii) 900
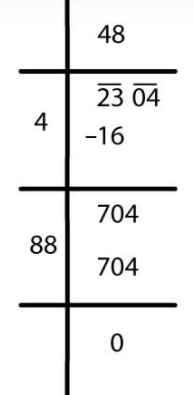
(i)
√2304 = 48
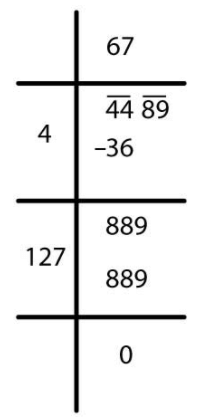
(ii)
√4489 = 67
(iii)
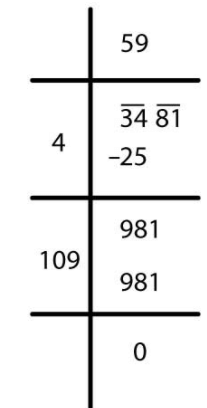
√3481 = 59
(iv)
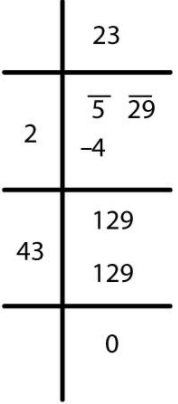
√529 = 23
(v)
√3249 = 57
(vi)
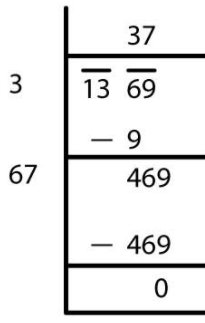
√1369 = 37
(vii)
√5776 = 76
(viii)
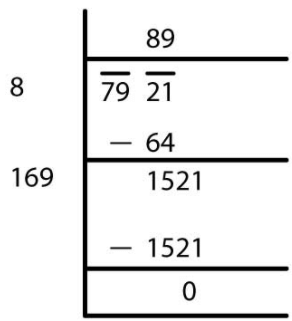
√7291 = 89
(ix)
√576 = 24
(x)
√1024 = 32
(xi)
√3136 = 56
(xii)
√900 = 30
Q.2. Find the number of digits in the square root of each of the following numbers (without any calculation).
(i) 64
(ii) 144
(iii) 4489
(iv) 27225
(v) 390625
If ‘n’ stands for the number of digits in the given number, then
(i) For 64, n = 2 [even number]
∴ Number of digit is its square root = n/2 = 2/2 = 1
(ii) For 144, n = 3 [odd number]
∴ Number of digits in its square root = n+1/2 = 3+1/2 = 4/2 = 2
(iii) For 4489, n = 4 [even number]
∴ Number of digits in its square root = n/2 = 4/2 = 2
(iv) For 27225, n = 5 [odd number]
∴ Number of digits in its square root = n+1/2 = 5+1/2 = 6/2 = 3
(v) For 390625, n = 6 [even number]
∴ Number of digits in its square root = n/2 =6/2 =3
Q.3. Find the square root of the following decimal numbers.
(i) 2.56
(ii) 7.29
(iii) 51.84
(iv) 42.25
(v) 31.36
(i) √2.56
Here, the number of decimal places is already even.
∴ We mark off the periods and find the square root.
∴ √2.56 = 1.6
(ii) √7.29
Here, the number of decimal places is already even.
Therefore, we mark off the periods and find the square root.
∴ √7.29 = 2.7
(iii) √51.84
Here, the decimal places are already even.
∴ We mark off the periods and find the square root.
∴ √51.84 = 7.2
(iv) √42.25
Here, the decimal places are already even.
∴ We mark off periods and find the square root.
∴ √42.25 = 6.5
(v) √31.36
Here, the decimal places are already even.
∴ We mark off the periods and find the square root.
∴ √31.36 = 5.6
Q.4. Find the least number that must be subtracted from each of the following numbers to get a perfect square. Also, find the square root of the perfect square so obtained.
(i) 402
(ii) 1989
(iii) 3250
(iv) 825
(v) 4000
(i) On proceeding to find the square root of 402, we have since we get a remainder 2
∴ The required least number to be subtracted from 402 is 2.
∴ 402 – 2 = 400, and √400 = 20
(ii) Since, we get a remainder of 53
∴ The least number to be subtracted from the given number = 53
1989 – 53 = 1936, and √1936 = 44
(iii) Since, we get a remainder 1.
∴ The smallest number to be subtracted from the given number = 1
Now, 3250 – 1 = 3249, and
(iv) Since, we get a remainder 41.
∴ The required smallest number to be subtracted from the given number = 41
Now, 825 – 41 = 784, and
(v) Since, we get a remainder 31,
∴ The required smallest number to be subtracted from the given number = 31
Now, 4000 – 31 = 3969, and
Q.5. Find the least number that must be added to each of the following numbers to get a perfect square. Also, find the square root of the perfect square so obtained.
(i) 525
(ii) 1750
(iii) 252
(iv) 1825
(v) 6412
(i) Since, we get a remainder of 41.
i.e. 525 > 222.
and the next square number is 23.
∴ The required number to be added = 232 – 525
= 529 – 525 = 4
Now, 525 + 4 = 529, and
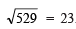
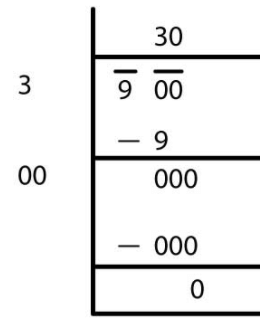
(ii) Since, we get a remainder 69.
i.e. 1750 > (41)2
and next square number is 422.
∴ The required number to be added = 422 – 1750
= 1764 – 1750 = 14
Now, 1750 + 14 = 1764, and
(iii) Since, we get a remainder 27.
Since, 252 > (15)2 and next square number = 16
∴ The required number to be added = 162 – 252
= 256 – 252 = 4
Now, 252 + 4 = 256, and
(iv) Since, we get a remainder, 61.
∴ 1825 > (42)2
∵ Next square number = 43
∴ The required number to be added = (43)2 – 1825
⇒1849 – 1825 = 24
Now, 1825 + 24 = 1849, and
(v) Since, we get a remainder 12.
∴ 6412 > (80)2
∵ Next square number = 81
∴ Required number to be added = (81)2 – 6412
⇒ 6561 – 6412 = 149
Now, 6412 + 149 = 6561 and
Q.6. Find the length of the side of a square whose area is 441 m2.
Let the side of the square = x meter
∴ Area = side * side
= x * x = x2 metre2
⇒
Thus, the required side is 21 m.
Q.7. In a right triangle ABC, ∠B = 90°.
(a) If AB = 6 cm, BC = 8 cm, find AC.
(b) If AC = 13 cm, BC = 5 cm, find AB.
Remember
I. In a right triangle, the longest side is called the hypotenuse.
II. (Hypotenuse)2 = [Sum of the squares of other two sides](a) ∵ ∠B = 90°
∴ Hypotenuse = AC
∴ AC2 = AB2 + BC2
⇒82 + 62
⇒64 + 36 = 100
AC = 10
Thus, AC = 10 cm
(b) Here ∠B = 90°
∴ Hypotenuse = AC
∵ AC2 = AB2 + BC2
⇒132 = AB2 + 52
⇒ AB2 = 132 – 52
= 169 – 25 = 144
Now
or AB = 12
Thus, AB = 12 cm
Q.8. A gardener has 1000 plants. He wants to plant these so that the number of rows and the number of columns remain the same. Find the minimum number of plants he needs more for this.
Since the number of plants in a row and the number of columns are the same.
∴ Their product must be a square number.
∵ The gardener has 1000 plants.
∴ 1000 is not a perfect square, and (31)2 < 1000
(∵ There is a remainder of 39).
Obviously the next square number = 32
∴ Number of plants required to be added = (32)2 – 1000
⇒1024 – 1000 = 24
Q.9. There are 500 children in a school. For a P.T. drill, they have to stand in such a manner that the number of rows is equal to the number of columns. How many children would be left out in this arrangement?
Since the number of rows and the number of columns are same.
∴ The total number (i.e. their product) must be a square number, we have Since, we get a remainder of 16
∴ 500 > (22)2 or 500 – 16 = (22)2
Thus, the required number of children to be left out = 16
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Squares and Square Roots- 2
| 1. What is a perfect square? |  |
| 2. How can we find the square root of a number? |  |
| 3. What is the difference between square and square root? |  |
| 4. What is the importance of squares and square roots in mathematics? |  |
| 5. How can we simplify expressions involving squares and square roots? |  |