Area and its Boundary Class 5 Notes Maths Chapter 11
| Table of contents |

|
| What is Area? |

|
| Area of Rectangle and Square |

|
| Perimeter of Rectangle and Square |

|
| Units |

|
| Scale of drawing |

|
| Relationship between Area and Perimeter |

|
| Area when we cut the image |

|
2D Figure
- 2D shapes are flat shapes that have width and height.
- They're like drawings on a piece of paper.
- We can't hold them because they don't have depth.
 2D Figures
2D Figures - 2D means "two-dimensional," which just means they have two measurements: width and height.
- Dimensions are like the size of a shape in different directions, but 2D shapes only have width and height, not depth.
What is Area?
- The area is how much space a flat shape takes up.
- It's like counting how many small squares fit inside a shape.
- We measure area using square units like cm² or m².
- Shapes like circles, triangles, squares, and rectangles all have area.
Area is the space inside the lines that make up a shape.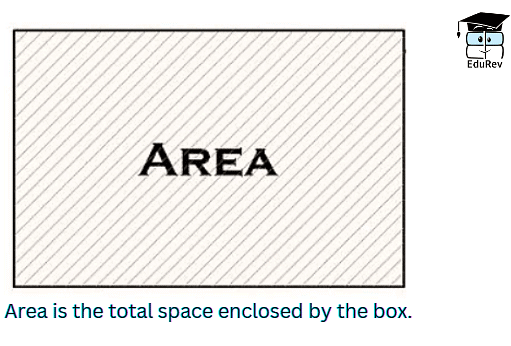
Area of Rectangle and Square
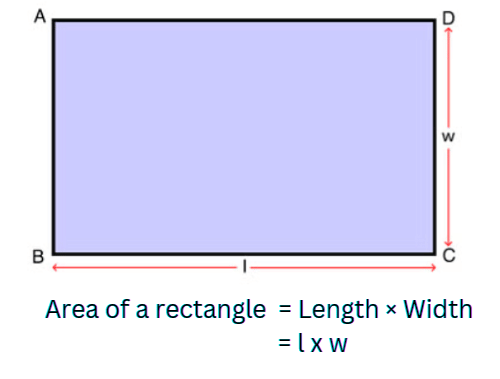
Area of a Rectangle
- The area of a rectangle is how much space it takes up inside.
- You find the area by multiplying the length and width of the rectangle.
- The formula for the area of a rectangle is: Area = length × width.

- It's like counting how many unit squares fit inside the rectangle.
- So, if a rectangle has a length of 'l' and a width of 'w', the area is 'l' times 'w'.
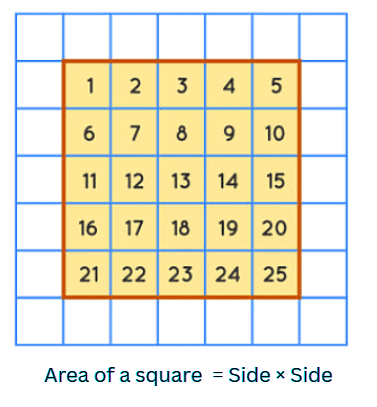
Area of a Square
- The area of a square is how much space it takes up inside.
- You find the area by multiplying the length of one side by itself.
- The formula for the area of a square is Area = side × side.

- The unit of area is given in square units.
- For example, if a square has a side length of 5 units, its area is 5 × 5 = 25 square units.
- This means if you count the squares inside, it tells you how much space the square covers.
Example 1: If the length of the board is 12 cm and the breadth is 10 cm and we want to cover the board with square sheets. The side of the square sheet is 2 cm. How many sheets are required to cover the board?
Sol: Length of board = 12 cm
Breath of board = 10 cm
Area of board = length x breadth
⇒ Area of board = (10 x 12) cm2
⇒ Area of board = 120 cm2
Side of sheet = 2 cm
Area of sheet = side × side
⇒ Area of sheet = (2 × 2) cm2
⇒ Area of sheet = 4 cm2
Number of sheets required = Area of board / Area of sheet
⇒ Number of sheets required = 120 / 4
⇒ Number of sheets required = 30
Example 2: Calculate the length and breadth of the rectangle whose area is 512 cm2 and the length is twice the breadth.
Sol: Let the breadth of the rectangle be x, and then the length will be 2x.
Area of rectangle = x × 2x = 512
⇒ 2x2 = 512
⇒ x2 = 512/2 = 256
⇒ x2 = 256
⇒ x = 16
Thus, the breadth is 16 cm, and the length is 32 cm.
Example 3: If the area of a square is 289 cm2, then find the measure of its side.
Sol: Let a be the side of a square.
We know that the area of a square with side “a” = a2
So, a2 = 289 cm2 (given)
⇒ a = 17 cm
Hence, the measure of the side of the square is 17 cm.
Perimeter of Rectangle and Square
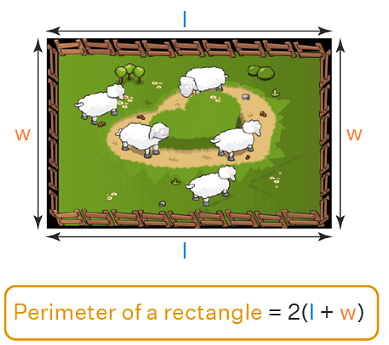
Perimeter of Rectangle
- The perimeter of a rectangle is how long the boundary is all around.
- We can find the perimeter by adding up the lengths of all four sides.
- The formula for the perimeter of a rectangle is Perimeter = 2 × (length + width).
- Imagine walking around the edges of a farm – you're measuring the perimeter.
- If the length of the farm is 'l' and the width is 'w', the perimeter is 2 times the sum of 'l' and 'w'.
Perimeter of Square
- The perimeter of a square is how long the whole edge is all around.
- You find the perimeter by adding up the lengths of all four sides.
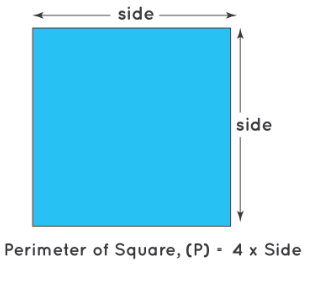
- The formula for the perimeter of a square is Perimeter = 4 times the length of one side.
- It's like adding up how much all the sides of the square measure altogether.
Example 1: It is known that the area of a square is 81 cm2. Find the perimeter of the square.
Sol: Area =81 cm2
Area = side × side
⇒ 81= (a)2
⇒ (9)2 = (a)2
⇒ 9 cm = a
⇒ Perimeter = 4 × side
⇒ Perimeter = 4 × 9
⇒ Perimeter = 36 cm
Example 2: A bedsheet has a length of 120 inches and a breadth of 95 inches. How much lace will be required to complete the border?
Sol: The perimeter of the bed sheet will be determined using the perimeter of the rectangle formula to determine the amount of lace required for the bedsheet’s border.
Given,
Length, l = 120 inches
Breadth, b = 95 inches.
As we know, the perimeter of a rectangle = 2(l + b) units.
Substituting the values in the formula, we get
Perimeter = 2(120 + 95) = 2 × 215 = 430 inches.
Hence, we will need 430 inches of lace to complete the border.
Example 3: Find the length of the sides of the square park, whose perimeter is 232 m.
Sol: Perimeter of square park = 4 × side = 232 m
⇒ side = 232/4
⇒ side = 58 m.
Therefore, the length of the sides of the square park is 58 m.
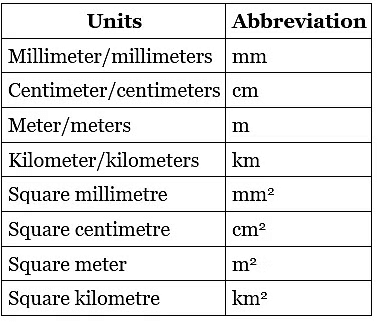
Units
- A unit of measurement is a definite magnitude of a quantity that is adopted by law and is used as a standard for measuring the same type of quantity.
- We measure the perimeter of any figure in mm, cm, m, or km.
- We measure the area of any figure in mm square, cm square, m square, or km square.
Measurement Abbreviations and their Comparisons
Millimeter (mm):
- This is a tiny measurement, like the thickness of a paperclip wire.
- Example: The width of a small button might be a few millimeters.
Centimeter (cm):
- A bit bigger than millimeters, like the width of your fingernail.
- Example: The length of a small toy car could be a few centimeters.
Meter (m):
- This is bigger, like the height of a door or the length of a desk.
- Example: The height of a basketball hoop is a few meters.
Kilometer (km):
- A very large measurement, like the distance between your home and school.
- Example: The distance from one town to another might be a few kilometers.

Square Millimeter (mm2):
- Imagine a tiny square made by connecting four dots, each one a millimeter apart on each side.
- Example: The area of a small sticker might be measured in square millimeters.
Square Centimeter (cm2):
- A bit bigger than the square millimeter, like a small square on a piece of paper.
- Example: The size of a postage stamp might be a few square centimeters.
Square Meter (m2):
- Larger than the square centimeter, like the floor space in a room.
- Example: The area of a small kitchen might be a few square meters.
Square Kilometer (km2):
- This is very big, like the area of a city or a large park.
- Example: The size of a big national park might be measured in square kilometers.
Always remember 1 mm < 1 cm < 1 m < 1 km. Similarly, 1 mm2 < 1 cm2 < 1 m2 < 1 km2
Scale of drawing
- A drawing of a real object reduced or enlarged by a certain amount (called the scale).
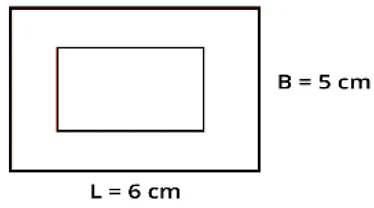
- Example: A garden with a paved border is shown below. 1 cm on this garden is equal to 100 m on the ground.
 Rectangular garden
Rectangular garden
Let’s find the length and breadth of the garden on the ground.
Length will be 6 x 100 m = 600 m.
Breadth will be 5 x 100 m = 500 m.
Relationship between Area and Perimeter
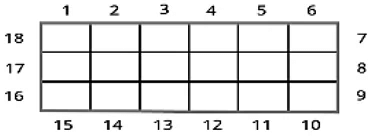
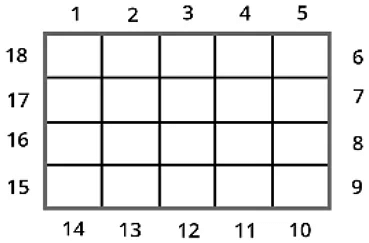
- Consider two rectangles A and B having the same perimeter as 18 units.


- Observe that both of them have different areas (Area of Rectangle A = 18 square units whereas Area of Rectangle B is 20 square units)


Hence we conclude that:
- The two shapes having the same perimeter can have different areas.
- Similarly, two shapes having the same areas can have different perimeters.
Area when we cut the image
- If we cut any 2D figure then the area of that 2D figure will be equal to the area of pieces. For example, if we cut a polygon into three pieces then the area of the polygon is equal to the sum of the area of three pieces.
 Before Cutting
Before Cutting
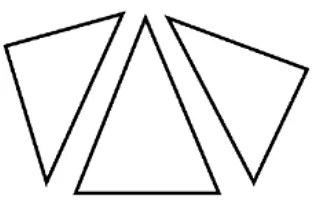 After Cutting
After Cutting
Example: Take a sheet of paper with a length of 14 cm and a breadth of 5 cm. Now cut this sheet into 5 equal rectangles. Find the area of each smaller rectangle.
Area of a sheet of length 14 cm and breadth 5 cm = Sum of the area of five equal rectangles
Area of sheet of length 14 cm and breadth 5 cm = 5 x (area of small rectangle)
⇒ 14 x 5 = 5 x (area of small rectangle)
⇒ Area of small rectangle = (14 x 5) / 5
⇒ Area of small rectangle = 14 cm2
The area of each smaller rectangle is 14 cm2.
|
28 videos|169 docs|41 tests
|
FAQs on Area and its Boundary Class 5 Notes Maths Chapter 11
| 1. What is the definition of area in a 2D figure? |  |
| 2. How do you calculate the area of a rectangle and a square? |  |
| 3. What is the formula to find the perimeter of a rectangle and a square? |  |
| 4. Why are units important when measuring area and perimeter? |  |
| 5. What is the relationship between area and perimeter in 2D figures? |  |

|
Explore Courses for Class 5 exam
|

|