NCERT Solutions for Class 8 Maths Chapter 3 - Understanding Quadrilaterals - 4 (Exercise 3.4)
Exercise 3.4
Q1. State whether True or False.
(a) All rectangles are squares.
(b) All rhombuses are parallelograms.
(c) All square are rhombuses and also rectangles.
(d) All squares are not parallelograms.
(e) All kites are rhombuses.
(f) All rhombuses are kites.
(g) All parallelograms are trapeziums.
(h) All squares are trapeziums.
Ans:
(a) False
Reason : Rectangles have opposite sides of equal length and all angles are 90 degrees, while squares have all sides of equal length and all angles are 90 degrees. Therefore, not all rectangles are squares.
(b) True
Reason : A rhombus is a type of parallelogram with all sides of equal length. Therefore, all rhombuses are also parallelograms.
(c) True
Reason : A square is a special case of both a rhombus and a rectangle. It has all sides of equal length (making it a rhombus) and all angles are 90 degrees (making it a rectangle).
(d) False
Reason : All squares are actually parallelograms. A square is a type of parallelogram with all sides of equal length and all angles equal to 90 degrees.
(e) False
Reason : While all kites have two pairs of adjacent sides that are equal, not all kites have all sides equal. A rhombus has all sides equal, so it is a specific type of kite, but not all kites are rhombuses.
(f) True
Reason : A rhombus is a type of kite due to its two pairs of adjacent sides being equal. Therefore, not all rhombuses are kites.
(g) True
Reason :A trapezium (also known as a trapezoid in some regions) is a quadrilateral with at least one pair of parallel sides. Since a parallelogram has both pairs of opposite sides parallel, it can also be considered a trapezium.
(h) True
Reason : A square is a type of parallelogram because it has both pairs of opposite sides parallel. Therefore, all squares are also trapeziums.
Q2. Identify all the quadrilaterals that have:
(a) Four sides of equal length.
(b) Four right angles.
Ans: (a) Squares as well as rhombus have four sides of equal length.
(b) Squares as well as rectangles have four right-angles.
Q3. Explain how a square is:
(i) a quadrilateral
(ii) a parallelogram
(iii) a rhombus
(iv) a rectangle
Ans:
(i) A square is a 4 sided figure, so it is a quadrilateral.
(ii) The opposite sides of a square are equal and parallel, so it is a parallelogram.
(iii) All the sides of a square are equal, so it is a rhombus.
(iv) Each angle of a square is a right angle, so it is a rectangle.
Q4. Name the quadrilaterals whose diagonal:
(i) bisect each other
(ii) are perpendicular bisectors of each other
(iii) are equal
Ans: (i) The diagonals of the following quadrilaterals bisect each other:
Parallelogram, rectangle, square, rhombus
(ii) The diagonals are perpendicular bisectors of the following quadrilaterals:
Square and rhombus
(iii) The diagonals are equal in case of:
Square and rectangle
Q5. Explain why a rectangle is a convex quadrilateral.
Ans: (i) All the angles have measures less than 180°.
(ii) Both diagonals lie wholly in the interior of the rectangle.
∴ The rectangle is a convex quadrilateral.
Q6. ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).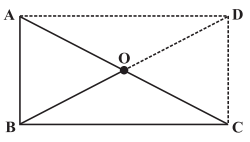
Ans: Produce BO to D such that BO = OD.
Joining CD and AD, we get a quadrilateral ABCD in which opposite sides are parallel.
∴ ABCD is a parallelogram.
∵ ∠ABC = 90°
∴ ABCD is a rectangle.
Since, diagonals of a rectangle bisect each other, i.e. O is the mid-point of BD and AC
∴ O is equidistant from A, B and C.
|
41 videos|48 docs|9 tests
|
FAQs on NCERT Solutions for Class 8 Maths Chapter 3 - Understanding Quadrilaterals - 4 (Exercise 3.4)
| 1. What are quadrilaterals? |  |
| 2. How many types of quadrilaterals are there? |  |
| 3. What is the sum of the interior angles of a quadrilateral? |  |
| 4. How do you determine if a quadrilateral is a rectangle? |  |
| 5. How do you find the area of a parallelogram? |  |

















