Chapter 18 - Practical Geometry (Constructions) (Part - 3), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 18.4:
Question 1:
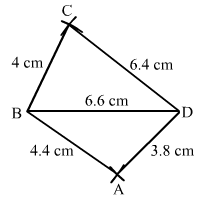
Construct a quadrilateral ABCD in which AB = 4.4 cm, BC = 4 cm, CD = 6.4 cm, DA = 3.8 cm and BD = 6.6 cm.
ANSWER:
First, we draw a rough sketch of the quadrilateral ABCD and write down its dimensions along the sides.
We may divide the quadrilateral into two constructible triangles ABD and BCD.
Steps of Construction:
Step I: Draw BD = 6.6 cm
Step II: With B as the centre and radius BC = 4 cm, draw an arc.
Step III: With D as the centre and radius 6.4 cm, draw an arc to intersect the arc drawn in Step II at C.
Step IV: With B as the centre and radius 4.4 cm, draw an arc on the side BD opposite to that of C.
Step V: With D as the centre and radius 3.8 cm, draw an arc to intersect the arc drawn in Step IV at A.
Step VI: Join BA, DA, BC and CD
The quadrilateral ABCD so obtained is the required quadrilateral.
Question 2:
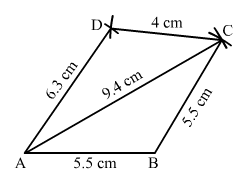
Construct a quadrilateral ABCD such that AB = BC = 5.5 cm, CD = 4 cm, DA = 6.3 cm and AC = 9.4 cm. Measure BD.
ANSWER:
Steps of construction:
Step I: Draw AB = 5.5 cm
Step II: With B as the centre and radius BC = 5.5 cm, draw an arc.
Step III: With A as the centre and radius AC = 9.4 cm,
draw an arc to intersect the arc drawn in Step II at C.
Step IV: With C as the centre and radius CD = 4 cm, draw an arc.
Step V: With A as the centre and radius AD = 6.3 cm,
draw an arc to intersect the arc drawn in Step IV at D.
Step VI: Join DA, BC, AC and CD.
The quadrilateral ABCD so obtained is the required quadrilateral.
Question 3:
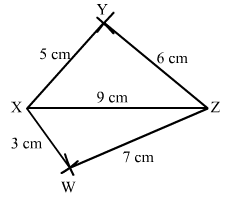
Construct a quadrilateral XYZW in which XY = 5 cm, YZ = 6 cm, ZW = 7 cm, WX = 3 cm and XZ = 9 cm.
ANSWER:
Steps of construction:
Step I: Draw XZ = 9 cm
Step II: With X as the centre and radius 5 cm, draw an arc above XZ.
Step III: With Z as the centre and radius 6 cm, draw an arc to intersect the arc drawn in Step II at Y above XZ.
Step IV: With Z as the centre and radius 7 cm, draw an arc below XZ.
Step V: With X as the centre and radius 3 cm, draw an arc to intersect the arc drawn in Step IV at W below XZ.
Step VI: Join XY, YZ, ZW and XW.
The quadrilateral WXYZ so obtained is the required quadrilateral.
Question 4:
Construct a parallelogram PQRS such that PQ = 5.2 cm, PR = 6.8 cm and QS = 8.2 cm.
ANSWER:
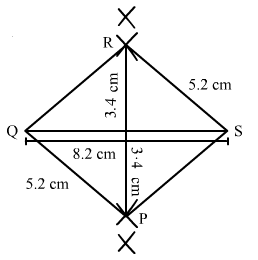
In a parallelogram opposite sides are equal.
Thus, we have to construct a quadrilateral PQRS in which
PQ = 5.2 cm,
PR = 6.8 cm and QS = 8.2 cm.
Steps of construction:
Step I: Draw QS = 8.2 cm
Step II: With Q as the centre and radius 5.2 cm, draw an arc.
Step III: With S as the centre and radius 5.2 cm, draw an arc to intersect the arc drawn in Step II at C.
Step IV: With P as the centre and radius 6.8 cm.
Step V: With Q as the centre and radius 5.2 cm, draw an arc to intersect the arc drawn in Step IV at A.
Step VI: Join QR, QP, PS and SR.
The quadrilateral PQRS so obtained is the required quadrilateral.
Question 5:
Construct a rhombus with side 6 cm and one diagonal 8 cm. Measure the other diagonal.
ANSWER:
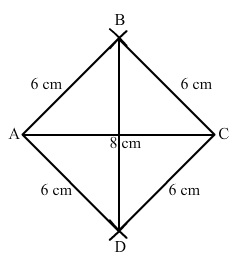
Steps of construction:
Step 1: Draw AC = 8 cm.
Step 2: With A as the centre and radius = 6 cm, draw arcs on both sides.
Step 3: With C as the centre and radius = 6 cm,
draw arcs on both sides, intersecting the previous arcs at points B and D.
Step 4: Join BD = 8.9cm.
Thus, ABCD is the required rhombus.
Question 6:
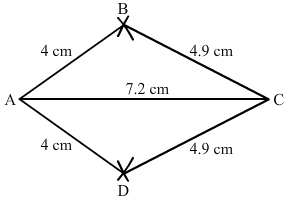
Construct a kite ABCD in which AB = 4 cm, BC = 4.9 cm and AC = 7.2 cm.
ANSWER:
Steps of construction:
Step I: Draw AC = 7.2 cm.
Step II: With A as the centre and radius 4cm, draw arcs on both sides of the line segment AC.
Step III : With C as the centre and radius 4.9 cm, draw arcs on both sides of AC intersecting the previous arcs of step II at B and D.
Step IV: Join BA, DA, BC and CD.
Thus, the quadrilateral ABCD so obtained is the required kite.
Question 7:
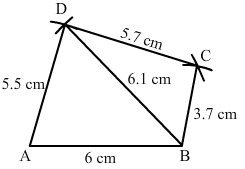
Construct, if possible, a quadrilateral ABCD given AB = 6 cm, BC = 3.7 cm, CD = 5.7 cm, AD = 5.5 cm and BD = 6.1 cm. Give reasons for not being able to construct it, if you cannot.
ANSWER:
Steps of construction:
Step I: Draw AB = 6 cm.
Step II: With A as the centre and radius 5.5 cm, draw an arc.
Step III : With B as the centre and radius 6.1 cm, draw an arc to intersect the arc drawn in StepII at D.
Step IV: With B as the centre and radius 3.7 cm, draw an arc on the side.
Step V :With D as the centre and radius 5.7 cm, draw an arc to intersect the arc drawn in StepIV at C.
Step VI: Join BD, DA, BC and CD.
The quadrilateral ABCD so obtained is the required quadrilateral.
Question 8:
Construct, if possible, a quadrilateral ABCD in which AB = 6 cm, BC = 7 cm, CD = 3 cm, AD = 5.5 cm and AC = 11 cm. Give reasons for not being able to construct, if you cannot. (Not possible, because in triangle ACD, AD + CD < AC).
ANSWER:
Such a quadrilateral cannot be constructed because in a triangle, the sum of the length of its two sides must be greater than the that of the third side
But here in triangle ACD,
AD + CD = 5.5 + 3 = 8.5 cm
and AC = 11 cm
i.e., AD + CD < AC, which is not possible.
So, the construction is not possible.
FAQs on Chapter 18 - Practical Geometry (Constructions) (Part - 3), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What are the different types of constructions discussed in Chapter 18 of RD Sharma Solutions for Class 8 Maths? |  |
| 2. How do you construct the perpendicular bisector of a line segment using the steps given in RD Sharma Solutions for Class 8 Maths? |  |
| 3. How can I construct an angle bisector using the steps provided in RD Sharma Solutions for Class 8 Maths? |  |
| 4. Can you explain how to construct a perpendicular from a point to a line using the steps given in RD Sharma Solutions for Class 8 Maths? |  |
| 5. How do you construct a triangle when its base, sum/difference of the other two sides, and one base angle are given, as explained in RD Sharma Solutions for Class 8 Maths? |  |
















