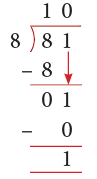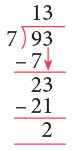Factors and Multiples Class 4 Notes Maths
| Table of contents |

|
| Factors |

|
| Finding Factors |

|
| Common Factors |

|
| Multiples |

|
| Common Multiples |

|
| Sieve of Eratosthenes |

|
| Prime Factorisation |

|
| Divisibility Rules |

|
Factors
For a dance competition, 16 dancers have to perform on the stage together. The choreographer drew the different ways they could do it, as shown below.
1.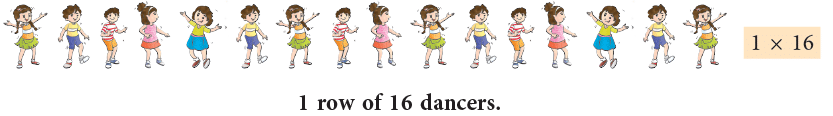 2.
2.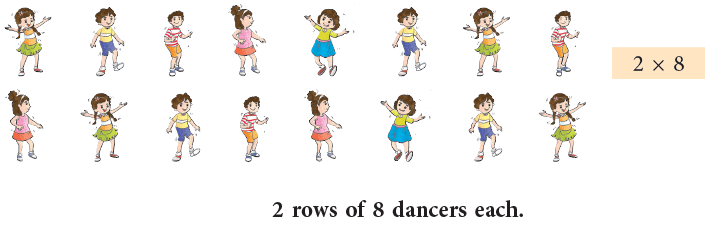 3.
3.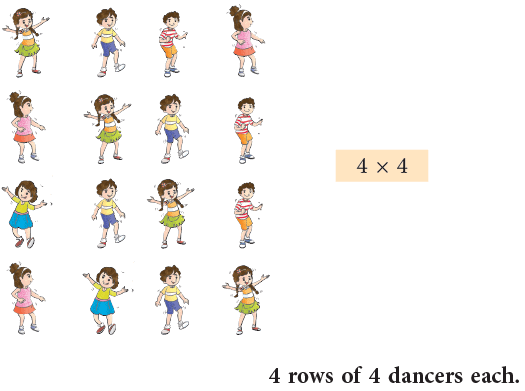
- The first way can be shown as 1 × 16.
- The second way it can be shown as is 2 × 8. The third way is 4 × 4.
- We see that different numbers can be multiplied to get the same product. The numbers that are multiplied to get a product are called the factors of the product.
- So, we can say that 1, 2, 4, 8 and 16 are all factors of 16. These numbers divide the number 16 completely.
“Factors” are the numbers you multiply to get another number. Factors of a number divide the number completely.
Finding Factors
We can find the factors of a number by any two methods:
1. By Multiplication
Let us find the factors of 24.
We have:
1 × 24 = 24,
2 × 12 = 24,
3 × 8 = 24,
4 × 6 = 24
Clearly, 1, 2, 3, 4, 6, 8, 12 and 24 are all the factors of 24 in ascending order.
2. By Division
24 ÷ 1 = 24,
24 ÷ 2 = 12,
24 ÷ 3 = 8,
24 ÷ 4 = 6 ,
24 ÷ 6 = 4,
24 ÷ 8 = 3,
24 ÷ 12 = 2,
24 ÷ 24 = 1
The numbers 1, 2, 3, 4, 6, 8, 12 and 24 divide the number 24 exactly. So, 1, 2, 3, 4, 6, 8, 12 and 24 are all factors of 24.
Example 1: Is 3 a factor of 54?
Sol: When we divide 54 by 3, we get a remainder of zero.
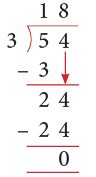
Thus, 3 is a factor of 54, as it divides 54 without a remainder.
Example 2: Is 8 a factor of 81?
Thus, 8 is not a factor of 81, as it does not divide 81 exactly.
Properties of Factors
- 1 is a factor of every number. It is also the smallest factor of a number.
Example: 1 is a factor of 1, 2, 3, 4, 5, ... - Every number (other than 1) has at least 2 factors, 1 and the number itself.
Example: 2 has 2 factors, 1 and 2, whereas 6 has 4 factors, 1, 2, 3 and 6. - The factor of a number is less than or equal to the number.
- A number is its own largest factor.
Example: 15 is the largest factor of 15. - A number has a limited number of factors.
Example: 6 has 4 factors, 1, 2, 3 and 6. It has no more factors.
Common Factors
The numbers which are common among the factors of two or more numbers are called the common factors.
(a) Find the common factors of 9 and 15.
Since 9 = 1 × 9 = 3 × 3.
Factors of 9 are 1, 3 and 9.
Since 15 = 1 × 15 = 3 × 5.
Factors of 15 are 1, 3, 5 and 15.
We can see that factors 1 and 3 appear in both the lists of factors.
So, 1 and 3 are common factors of 9 and 15.
(b) Find the common factors of 12 and 18.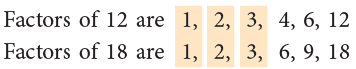
Clearly, the common factors of 12 and 18 are 1, 2 and 3.
Multiples
Consider the multiplication, 7 × 8 = 56. We call 7 and 8 factors and 56, the product. Another name for the product is multiple.
Look at the multiplication table of 2 given below:
2, 4, 6, 8, 10, 12, 14, 16, 18 are the first 9 multiples of 2. These multiples of 2 have been obtained by multiplying 2 by the counting numbers 1, 2, 3, ..., 9.
Thus, a multiple of 2 is a product of 2 and another counting number.
A multiple of a number is the product of the given number and some other counting numbers.
Properties of Multiples
1. Every number is a multiple of 1.
Examples: 5 × 1 = 5, 13 × 1 = 13, 108 × 1 = 108
2. Every number is a multiple of itself.
3. Every multiple of a counting number is either greater than or equal to the number.
Example: The first four multiples of 4 are 4, 8, 12, 16.
4. The first and the smallest multiple of a number is the number itself.
5. There are infinite multiples of a number. So, the largest multiple of a number cannot be determined.
Edurev Tips: To check if bigger number is a multiple of the smaller number, we divide the bigger number by the smaller number. If the remainder is 0, it means the bigger number is a multiple of the smaller number.
Example 3: Is 93 a multiple of 7?
We check this by dividing 93 by 7.
Since remainder ≠ 0, 7 does not divide 93 exactly.
So, 93 is not a multiple 7.
Even and Odd Numbers
A number which is a multiple of 2 is an even number.
0, 2, 4, 6, 8, 10 and 12 are some of the even numbers.
Even numbers always end in one of the digits 0, 2, 4, 6 or 8.
Edurev Tips: Even numbers are exactly divisible by 2.
A number which is not a multiple of 2 is an odd number.
1, 3, 5, 7, 9, 11 and 15 are some of the odd numbers.
Odd numbers always end in one of the digits, 1, 3, 5, 7 or 9.
Common Multiples
The numbers which are common among the multiples of two or more numbers are called common multiples.
Let us find common multiples of 6 and 8.
Multiples of 6 are 6, 12, 18,  30, 36, 42,
30, 36, 42, ...
...
Multiples of 8 are 8, 16,  32, 40,
32, 40,  56, ...
56, ...
Common multiples of 6 and 8 are 24, 48, ...
Natural Numbers
The counting numbers 1, 2, 3, 4, ... are called natural numbers.
Whole Numbers
The natural numbers along with 0, i.e., 0, 1, 2, 3, 4, ... are called whole numbers.
Prime and Composite Numbers
1. Prime Numbers
A prime number is a natural number greater than 1, which has only two different factors, namely, 1 and the number itself.
Let us find all the factors of 2, 5 and 7.
Factors of 2 are 1 and 2.
Factors of 5 are 1 and 5.
Factors of 7 are 1 and 7.
Since each of the numbers 2, 5 and 7 has only two factors, they are prime numbers.
2. Composite Numbers
Numbers that have more than two factors are called composite numbers.
Let us find all the factors of 4, 6, 9.
Factors of 4 are 1, 2 and 4.
Factors of 6 are 1, 3 and 6.
Factors of 9 are 1, 3 and 9.
Since each of the numbers 4, 6 and 9 has more than two factors, they are composite numbers.
Edurev Tips:
- 1 is neither prime nor composite.
- 2 is the smallest prime number.
Sieve of Eratosthenes
About 250 BCE, a Greek mathematician, Eratosthenes, developed a method to find the prime numbers up to 100. In this method, we prepare a table of numbers from 1 to 100 and proceed as follows:
Step 1: Cross out 1 as it is neither prime nor composite.
Step 2: Encircle 2 and cross out all the multiples of 2.
Step 3: Encircle 3 and cross out all the multiples of 3.
Step 4: Encircle 5 and cross out all the multiples of 5.
Step 5: Encircle 7 and cross out all the multiples of 7.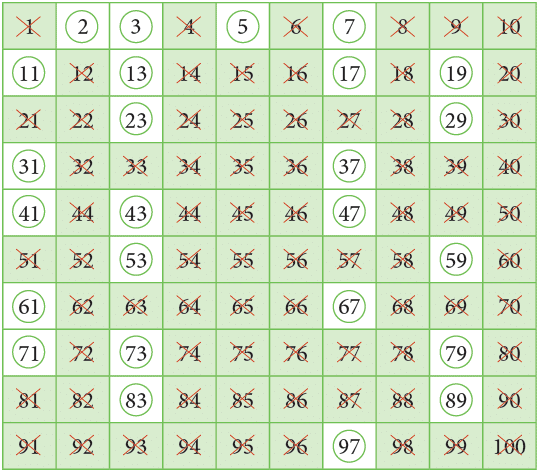 Now, encircle the numbers which are not crossed.
Now, encircle the numbers which are not crossed.
All of the encircled numbers are prime numbers.
Thus, all prime numbers from 1 to 100 are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 and 97.
You can see that there are 25 prime numbers from 1 to 100.
Edurev Tips: This method is called Sieve of Eratosthenes because factors are used to sift out certain numbers which are multiples as a sieve sifts out chaff from wheat. Finally, only the numbers which are not the multiples of any numbers remain in the list.
Prime Factorisation
There are several ways in which a given number may be factorised (broken into its factors).
For example, the number 36 can be factorised as,
36 = 4 × 9,
36 = 6 × 6,
36 = 1 × 36,
36 = 2 × 18,
36 = 3 × 12.
Here, we see that in all these cases either one factor is prime and the other is composite or both the factors are composite.
Is it possible to break 36 into factors which are all prime numbers? Let us see.
36 = 2 × 18 = 2 × 2 × 9 = 2 × 2 × 3 × 3.
These are all prime numbers.
The factors of a number which are prime are called prime factors.
When a number is written as a product of its prime factors only, then it is called prime factorisation.
Prime Factorisation of a Number
Prime factorisation can be done using two methods: The factor tree method and the division method.
Factor Tree Method
- To create a factor tree, we keep dividing a composite number into smaller factors.
- This process continues until we reach the smallest prime factors.
- A composite number is a number that can be divided by numbers other than one and itself.
- Prime factors are the basic building blocks of numbers, and they can only be divided by one and themselves.
- By breaking down a number into its factors, we can better understand its composition.
- The goal is to find the simplest parts of the number through repeated division.
- Look at the factor tree for the number 60 below:
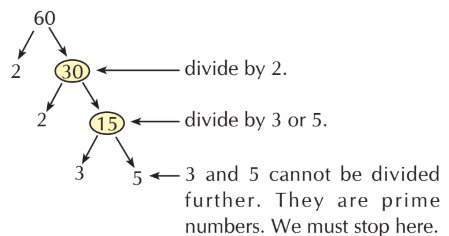
- Observe the following factor trees for the number 36.
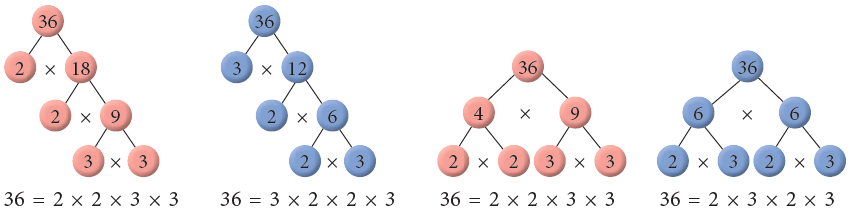 You can observe that whichever way the factorisation is done, you can see that the prime factors are the same.By convention, the prime factors are listed from the least to the greatest.
You can observe that whichever way the factorisation is done, you can see that the prime factors are the same.By convention, the prime factors are listed from the least to the greatest.
Thus, the prime factorisation of 36 is 2 × 2 × 3 × 3.
Division Method
Let us find prime factorisation of 24, 36 and 45.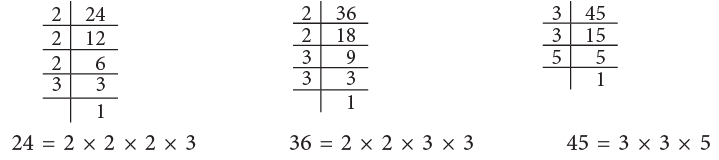 The steps to be followed in this method can be summarised as under:
The steps to be followed in this method can be summarised as under:
Step 1: Divide the given number by the smallest prime number that exactly divides it.
Step 2: Divide the quotient further by a prime number that exactly divides it.
Step 3: Continue the repeated division, till the remainder is not further divisible by any number.
Divisibility Rules
One number is divisible by another if it can be divided with no remainder. Here are some common rules which help us to find at a glance whether a given number is divisible by another number or not, without actually dividing it.
1. Divisibility by 2
A number is divisible by 2 if its last digit is an even number, i.e., the number ends in 0, 2, 4, 6 or 8.
For example: 6, 16, 44, 52, 118, 346 are all divisible by 2.
2. Divisibility by 3
A number is divisible by 3 if the sum of its digits is divisible by 3.
For example:
3. Divisibility by 5
A number is divisible by 5 if the digit at its ones place (last digit) is 0 or 5.
For example: 10, 15, 45, 60, 120, 155 are all divisible by 5.
4. Divisibility by 6
All numbers divisible by 2 and 3 both are divisible by 6.
A number will be divisible by 6 if its ones digit is an even number and the sum of its digits is divisible by 3.
For example:
5. Divisibility by 9
A number is divisible by 9 if the sum of its digits is divisible by 9.

6. Divisibility by 10
A number is divisible by 10 if the digit at its ones place (last digit) is 0.
For example: 30, 50, 110, 260, 1860 are all divisible by 10.
Edurev Tips: The numbers which are divisible by 10 are also divisible by 5.
|
33 videos|168 docs|30 tests
|
FAQs on Factors and Multiples Class 4 Notes Maths
| 1. What are factors, and how do you find them for a given number? |  |
| 2. What are common factors, and how can I find them for two numbers? |  |
| 3. What are multiples, and how can I determine the multiples of a number? |  |
| 4. What is the Sieve of Eratosthenes, and how does it help in finding prime numbers? |  |
| 5. What are the divisibility rules, and why are they important? |  |