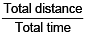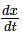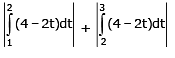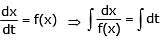Rest & Motion | Physics for EmSAT Achieve PDF Download
Rest and Motion
- An object is said to be in motion w.r.t a frame of reference S1, when its location is changing with time in the same frame of reference S1.
- Rest and motion are relative terms.
- Absolute rest and absolute motion have no meaning.
Motion is broadly classified into 3 categories.
- Rectilinear and translatory motion.
- Circular and rotatory motion.
- Oscillatory and vibratory motion.
Rectilinear or 1-D Motion
When a particle is moving along a straight line, then its motion is a rectilinear motion.
Parameters of rectilinear motion or translatory motion or plane motion:
(A) Time
- It is a scalar quantity and its SI unit is second(s).
- At a particular instant of time, a physical object can be present at one location only.
- Time can never decrease.
(B) Position or location
- It is defined with respect to some reference point (origin) of a given frame of reference.
- Consider a particle which moves from location r1 (at time t1) to location r2 (at time t2) as shown in the figure below, following path ACB.

(C) Distance
The length of the actual path traversed by the particle is termed as its distance.
Distance = length of path ACB.
- Its SI unit is metre and it is a scalar quantity.
- It can never decrease with time.
(D) Displacement
The change in position vector of the particle for a given time interval is known as its displacement.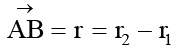
- Displacement is a vector quantity and its SI unit is metre.
- It can decrease with time.
For a moving particle in a given interval of time
- Displacement can be +ve, –ve or 0, but distance would be always +ve.
- Distance ≥ Magnitude of displacement.
- Distance is always equal to displacement only and only if particle is moving along a straight line without any change in direction.
(E) Average speed and average velocity
Average speed and average velocity are always defined for a time interval.
Average speed 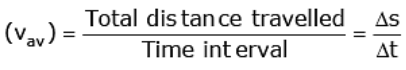
Average velocity 
- Average speed is a scalar quantity, while average velocity is a vector quantity. Both have the same SI units, i.e., m/s.
For a moving particle in a given interval of time
- Average speed can be a many valued function but average velocity would be always a single valued function.
- Average velocity can be positive, negative or 0 but average speed would be always positive.
(F) Instantaneous speed and instantaneous velocity
Instantaneous speed is also defined exactly like average speed i.e. it is equal to the ratio of total distance and time interval, but with one qualification that time interval is extremely (infinitesimally) small. The instantaneous speed is the speed at a particular instant of time and may have entirely different values than that of average speed. Mathematically.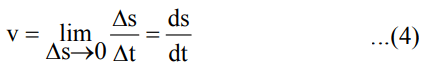
When Δs is the distance travelled in time Δt. As Δt tends to zero, the ratio defining speed becomes finite and equals the first derivative of the distance. The speed at the moment 't' is called the instantaneous speed at time 't'.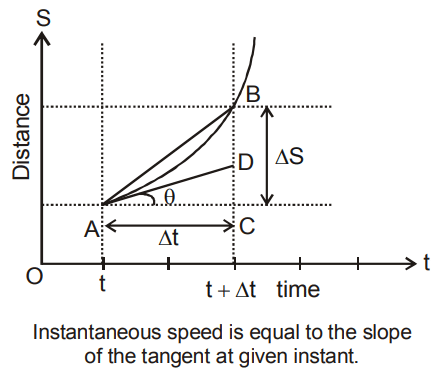
On the distance - time plot, the speed is equal to the slope of the tangent to the curve at the time instant 't'. Let A and B point on the plot correspond to the time t and t + Δt during the motion. As Δt approaches zero, the chord AB becomes the tangent AC at A. The slope of the tangent equals ds/dt, which is equal to the instantaneous speed at 't'.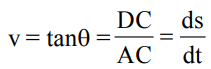
(G) Instantaneous velocity
Instantaneous velocity is defined exactly like speed. It is equal to the ratio of total displacement and time interval, but with one qualification that time interval is extremely (infinitesimally) small. Thus, instantaneous velocity can be termed as the average velocity at a particular instant of time when Δt tends to zero and may have entirely different values that of average velocity : Mathematically.
As Δt tends to zero, the ratio defining velocity becomes finite and equals the first derivative of the position vector. The velocity at the moment 't' is called the instantaneous velocity or simply velocity at time 't'.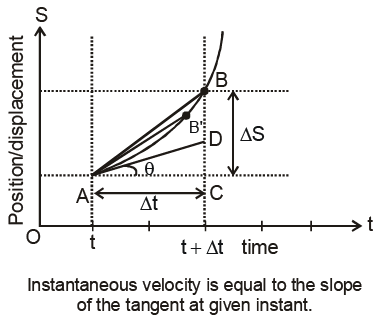
- The magnitude of average velocity |vavg| and average speed vavg may not be equal, but magnitude of instantaneous velocity |v| is always equal to instantaneous speed v.
Example 1: In 1.0 sec a particle goes from point A to point B moving in a semicircle of radius 1.0 m. The magnitude of average velocity is
(a) 3.14 m/sec
(b) 2.0 m/sec
(c) 1.0 m/sec
(d) zero
Sol:
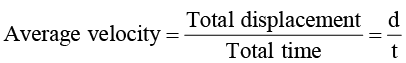
D = AO + OB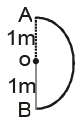
= 1 + 1 = 2m
t = 1 sec (given)
⇒ mg of v of 2/1 = 2m/sec
Example 2: A particle moves along a semicircular path of radius R in time t with constant speed. For the particle calculate
(i) distance travelled,
(ii) displacement,
(iii) average speed,
(iv) average velocity,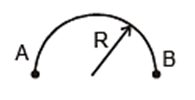
Sol: (i) Distance = length of path of particle = 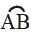 = πR
= πR
(ii) Displacement = minimum distance between initial and final point
= AB = 2R
(iii) Average speed, 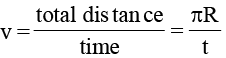
(iv) Average velocity = 2R/t
Example 3: A body travels the first half of the total distance with velocity v1 and the second half with velocity v2. Calculate the average velocity:
Sol: Let total distance = 2x. Then
total time taken = 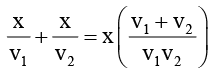
∴ Average speed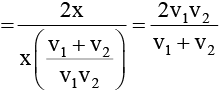
Example 4: Velocity-time equation of a particle moving in a straight line is, v = (10 + 2t + 3t2)
Find:
(a) displacement of particle from the origin of time t = 1 s, if it is given that displacement is 20 m at time t = 0
(b) acceleration-time equation.
Sol: (a) The given equation can be written as,
v = ds/dt = (10 + 2t + 3t2)
ds = (10 + 2t + 3t2) dt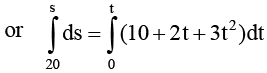
or s – 20 = [10t + t2 + t3]01
or s = 20 + 12 = 32 m
(b) Acceleration-time equation can be obtained by differentiating the given equation w.r.t. time.
Thus,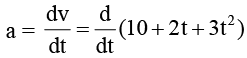
or a = 2 + 6t
Specimen Problem:
(A) When equation of displacement is given and speed to be find out
Example 5: If displacement is dependent on time such that x = 2t –2 then find out average speed upto 4 sec.
Sol. Average speed =
for Total distance
at t = 0 it is at x = – 2
at t = 1 it is at 0 m
at t = 4 it is at 6 m.
Total distance = |– 2| + 0 + 6 = 8 m
Average speed = 8/4 = 2m/sec
(B) When velocity is given as a function of time and distance to be find out
In this type of question first find out at what instant the velocity is zero. If this instant is come in our time limit then distance can be calculated by breaking the integration in two part with modulus
Example 6: If velocity is depend on time such that v = 4 – 2t. Find out distance travelled by particle from 1 to 3 sec.
Sol. Velocity is zero (4 – 2t = 0) at t = 2 sec
So for distance = 4 – 2t ⇒ dx =
dx = 1 + 1 = 2m
(G-1) When velocity is given as a function of t :
v = f(x) ⇒
Example 7: If velocity is given by following function V = x2. Then find out relation between x & t (assume x = 1 m at t = 0)
Sol. Relation between v & x is
v = x2
we know that v = 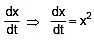
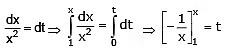

(E) Average and instantaneous acceleration.
When the velocity of a moving object/particle changes with time, we can say that it is accelerated.
Average acceleration,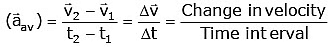
Instantaneous acceleration,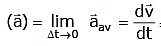 = Rate of change of velocity
= Rate of change of velocity
Acceleration is a vector quantity whose direction is same as that of change in velocity vector. Its SI unit is m/s2.
- When direction of acceleration and velocity are opposite to each other, then acceleration is termed as retardation.
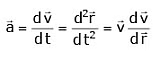
(E-1) When acceleration is given as a function of x
Example 8: if a = 2x ; initially particle is at x = 2m and is moving with 3 ms–1. Then find out v at x = 5 m.
Sol. Given a = 2x
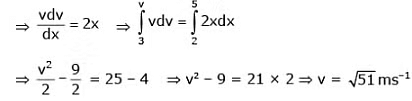
(E-2) When acceleration is given as function of velocity
Example 9: If a is depend on v in a following way. a = v and at t = 0 x = 1m, v = 1m/s.
(a) Find out its velocity at t = 2 sec.
(b) Find out its velocity at x = 3 m
Sol. Given a = v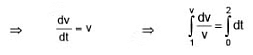
⇒ ln v = 2 ⇒ v = e2 ms–1
(b) Given a = v
(E-3) When acceleration is given as a function of t.
Example 10: The acceleration of a particle which is depend on time is given by following function a = 2t + 1 and at time t = 0, x = 1m and ui = 2m/s. Then find out displacement of the particle at t = 3 sec.
Sol. ∴ We know that a = ⇒ = 2t + 1 ⇒dv = (2t + 1) dt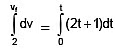
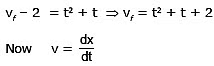
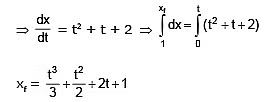
So, xf at t = 3 sec is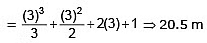
So, after t = 3 sec the position of the particle is 20.5m but the displacement of the particle is
= 20.5 – 1 = 19.5 m
(E-4) Constant Acceleration Format
Deduce the following equations for uniformly accelerated motion by using integration technique.
(A) v = u + at (B) 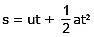
(C) v2 – u2 = 2as (D) 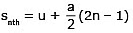
First equation of motion. Acceleration is defined as
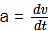
or dv = adt ...(1)
When time = 0, velocity = u (say)
When time = t, velocity = v (say)
Integrating equation (1) within the above limits of time and velocity, we get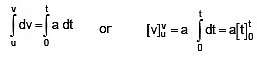
or v – u = a(t – 0)
or v = u + at ...(2)
Second equation of motion. Velocity is defined as
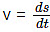
or ds = v dt = (u + at) dt ...(iii)
When time = 0, displacement travelled = 0
When time = t, displacement travelled = s (say).
Integrating equation (3) within the above limits of time and distance, we get
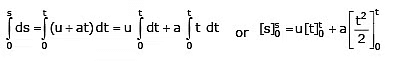
or s – 0 = u (t – 0) + 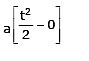
or s = ut + 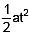 ...(4)
...(4)
Third equation of motion. By the definitions of acceleration and velocity,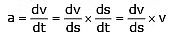
or ads = vdv ...(5)
When time = 0, velocity = u, displacement travelled = 0
When time = t, velocity = v, displacement travelled = s(say)
Integrating equation (5) within the above limits of velocity and displacement, we get
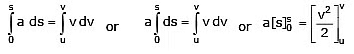
or 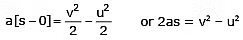
or v2 – u2 = 2as ...(6)
Fourth equation of motion. By definition of velocity,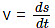
or ds = vdt = (u + at) dt ...(7)
When time = (n – 1) second, displacement travelled= sn – 1 (say).
When time = n second, displacement travelled = sn (say)
Integrating equation (7) within the above limits of time and distance, we get
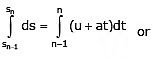
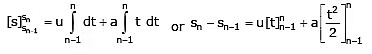
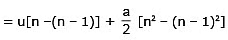
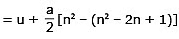

where snth = sn – sn –1 = displacement in nth second.
Example 11: A car starts from rest and accelerates uniformly for 20 seconds to a velocity of 72 km h–1. It then runs at constant velocity and finally brought to rest in 200 m with a constant retardation. The total distance covered is 600 m. Find the acceleration, retardation and the total time taken.
Sol. (i) Motion with uniform acceleration
Here, u = 0 ; t1 = 20 sec ; v = 72 × 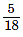 = 20 ms–1
= 20 ms–1
∴ v = u + at1
20 = 0 + a × 20 or a = 1 m s–2
Distance travelled by car in this time (20 sec),
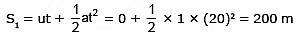
(ii) Motion with uniform velocity.
As given, total distance = 600 m
we have calculated S1 = 200 m (with uniform acceleration)
and S2 = 200 m (with retardation)
∴ Net distance for which body moves with uniform velocity,
S = 600 – S1 – S2
= 600 – 200 – 200 = 200 m
∴ Time taken, t = 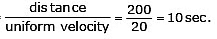
∴ Total time of journey, t = (20 + 10 + 20) sec
t = 50 sec
Average velocity = 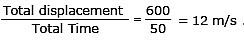
(iii) Motion with uniform retardation.
For this motion, initial velocity, u = 20 m s–1 and final velocity v = 0 ; S2 = 200 m
Acceleration a' = ?
Using, v2 – u2 = 2 a' S2
(0)2 – (20)2 = 2(a') × 200
a' = – 1 ms–2
Let t' = time for which the body comes to rest.
∴ v = u + a' t'
0 = 20 – 1t'
∴ t' = 20 sec.
C. specimen problem
Example 12: Find out distance travelled by the block in 10 sec. for a given situation.
Sol. First find out it what instant velocity of block becomes zero.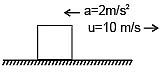
v = u + at
given : u = 10 m/s, a = – 2m/s2
⇒ 0 = 10 – 2t ⇒ t = 5 sec
So we calculate distance for two time intervals.
For first 5 sec.
S1 = ut – 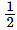 at2 ⇒ S1 = (10)(5) –
at2 ⇒ S1 = (10)(5) –  (2) (5)2 = 25 m
(2) (5)2 = 25 m
for Next 5 sec (block is travelling towards the starting point)
S2 = ut + 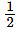 at2
at2
u = 0
S2 = 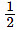 × 2 × 25 = 25 mS = S1 + S2 = 50 m
× 2 × 25 = 25 mS = S1 + S2 = 50 m
(D) Reaction time :
When a particular situation demands our immediate action, it takes some time before we really respond. Reaction time is the time a person takes to observe, think and act. For example, if a person is driving and suddenly a boy appears on the road, then the time elapse before he applies the breaks of the car is the reaction time. Reaction time depends on complexity of the situation and on an individual.
One can measure one's reaction time by a simple experiment. Take a rule and ask your friend to drop it vertically through the gap between your thumb and forefinger. As soon as it is dropped, note the time elapsed ts before you catch it and the distance d travelled by the ruler. (In a particular case, y was found to be 21.0 cm. Estimate reaction time).
Sol. As the ruler drops under free fall so u = 0, and g = 9.8 ms–2. The distance travelled d and the reaction time tr are related by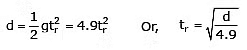 Here d = 21.0 cm = 0.21 m∴
Here d = 21.0 cm = 0.21 m∴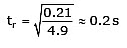
Note: Definition : Time taken by a driver to react for a situation
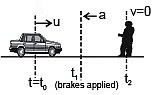
Reaction Time of the driver
is Δt = t1 – t0
Total distance covered by the car before stopping = distance covered in uniform motion during to to t1 + distance cover in de-accelerated motion during t1 to t2 =
Total distance = 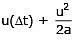
Example 13: Assume that a car is able to stop with a retardation of 8 ms–2 and that a driver can react to an emergency in 0.5 sec. Calculate the overall stopping distance of the car for a speed of 60 km–1 of the car.
Sol. Here, u = 60 km h–1 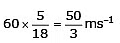
Since the application of brakes takes 0.5 s, before this the car was moving with uniform speed of 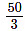 ms -1
ms -1
∴ Distance covered in 0.5 sec, with a uniform speed is
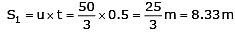
Now car begins to move with a retardation of 8ms–2
∴ Distance covered before coming to rest, 2a S2 = v2 – u2
or 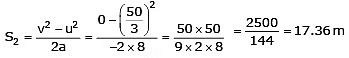
∴ Total (overall) distance = S1 + S2 = 8.33 + 17.36 ⇒ S = 25.69 m
Example 14: Two buses A and B are at positions 50 m and 100 m from the origin at time t = 0. They start moving in the same direction simultaneously with uniform velocity of 10 ms–1 and 5 ms–1. Determine the time and position at which A overtakes B.
Sol. Here we use equation of motion for constant velocity in Cartesian form.
Given x1 (0) = 50 m, x2 (0) = 100 m,
v1 = 10 ms–1, v2 = 5 ms–1
The positions of the two buses at any instant t are
x1 (t) = x1 (0) + v1t = 50 + 10 t
x2 (t) = x2 (0) + v2t = 100 + 10 t
When A overtakes B,
x1 (t) = x2 (t)
50 + 10t = 100 + 5t or 5t = 50
t = 10 s
x1 (10) = x2 (10) = 150 m
Thus A overtakes B at a position of 150 m from the origin at time t = 10 s.
Example 15: A bus starts from rest with constant acceleration of 5 ms–2. At the same time a car travelling with a constant velocity of 50 ms–1 overtakes and passes the bus.
(i) Find at what distance will the bus overtake the car ?
(ii) How fast will the bus be travelling then ?
Sol. (i) Suppose the bus overtakes the car after covering distance s.
When the two meet, time taken t is same.
For bus, 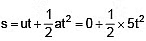
For car, s = 50 t
∴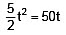 or t = 20 sHence s = 50 t = 50 × 20 = 1000 m.(ii) v2 = u2 + 2as = 0 + 2 × 5 × 1000 = 10,000 or v = 100 ms–1
or t = 20 sHence s = 50 t = 50 × 20 = 1000 m.(ii) v2 = u2 + 2as = 0 + 2 × 5 × 1000 = 10,000 or v = 100 ms–1
Specimen Problem
(E) Maximum Separation :
Example 16:  What is the maximum separation between car and scooter ?
What is the maximum separation between car and scooter ?
Sol. Initially separation between car & scooter increases and then decreases.
Separation between them will be maximum at an instant at which velocity of the car is equal to the velocity of scooter.
Velocity car = Velocity scooter = 40 m/s
from v = u + at
40 = 0 + 4t ⇒ t = 10 sec
The distance travelled by scooter in 10 sec.
is S1 = 10 × 40 = 400 m
The distance travelled by car in 10 sec. is
S2 = ut + 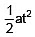 = 0 + × 4 × (10)2 = 200 m
= 0 + × 4 × (10)2 = 200 m
So maximum separation = S1 – S2 = 400 – 200 = 200 m
- When they meet both will travel the same distance.
|
208 videos|329 docs|212 tests
|
FAQs on Rest & Motion - Physics for EmSAT Achieve
| 1. What is the definition of rest and motion? |  |
| 2. What are the different types of motion? |  |
| 3. What is the difference between rest and motion? |  |
| 4. How can rest and motion be described mathematically? |  |
| 5. What are some everyday examples of rest and motion? |  |