Congruence of Triangle | Mathematics (Maths) Class 9 PDF Download
Congruent triangles class 7 helps the student to understand the concept of congruence of the triangle in a different perspective. It states that two triangles are said to be congruent if they are copies of each other and they cover each other exactly. Congruence of triangles class 7 helps the students to learn about some of the axiom rules that every student should be needed to know for proceeding their higher studies.
Congruent Triangles Class 7 Concepts
The major topics covered in congruent triangles class 7 are:
- Congruence of Triangles
- Congruence of Plane Figure
- Congruence among Line Segment
- Congruence of Angles
- Criteria for Congruence of Triangles
- Congruence among Right Angled Triangles
Congruent Triangles Class 7 Notes
Consider the triangle ABC and PQR,
Both have the same size and shape and they are said to be congruent. So, this can be expressed as
∆ABC ≅ ∆PQR
It is noted that, when you place a triangle PQR on triangle ABC, P falls on A, Q falls on B and R falls on C, also the side PQ falls alongside AB, QR falls along BC and PR falls along AC. Under a correspondence property, when two triangles are congruent, then their corresponding sides and angles match with one another are it must be equal. So, in these two congruent triangles, we have the congruences as follows
Corresponding vertices are A = P, B = Q, C = R.
Corresponding sides are AB = PQ, BC = QR , AC = PR .
Corresponding angles : ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R.
It is noted that while talking about the congruence of triangles, it is not only the measures of angles and lengths of sides, but also with the matching of vertices. In the above case, the correspondence is written as
A ↔ P, B ↔ Q, C ↔ R
We also we may write it as ABC ↔ PQR
Congruence of Triangle Criterion
The criteria for congruent triangles class 7 is explained using two axiom rules.
SSS Congruence Rule (Side – Side – Side)
The triangles are said to be congruent if all the three sides of one triangle are equal to the three corresponding sides of another triangle
Example: In the given triangles ABC and PQR, AB = 3.5 cm, BC = 7.1 cm, AC = 5 cm, PQ = 7.1 cm, QR = 5 cm and PR = 3.5 cm. Examine whether the given two triangles are congruent or not. If yes, then write the congruence relation in symbolic form.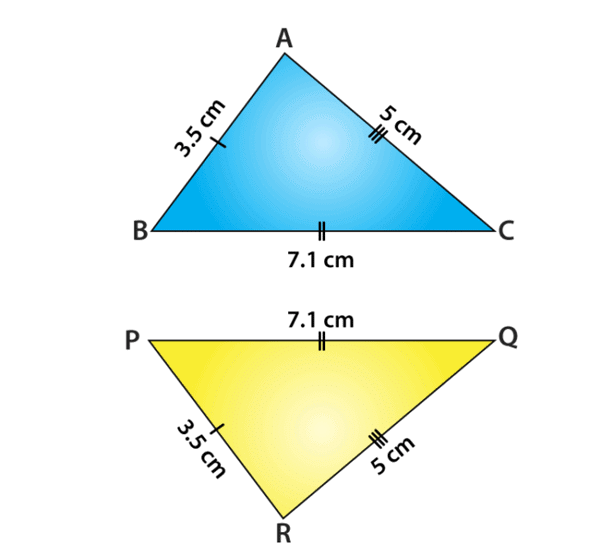
Solution:
Given : AB = PR = 3.5 cm
BC = PQ = 7.1 cm and
AC = QR = 5 cm
This shows that all the sides of one triangle are equal to all sides of the other triangle. By using SSS congruence rule, the two triangles are congruent. From the three equality relations, we can write it as
A↔R, B↔P, C↔Q
So, the congruence of triangles in symbolic form is ∆ABC ≅ ∆RPQ
SAS Congruence Rule( Side – Angle – Side)
The triangles are said to be congruent if the correspondence, two sides and the angle included between them of a triangle are equal to two corresponding sides and the angle included between them of another triangle.
Example: The measurements of some parts of two triangles are given below. Check whether the two triangles are congruent or not, using SAS congruence rule. Write it in symbolic form, if the triangles are congruent. For ∆ABC, AB = 7 cm, BC = 5 cm, ∠B = 50° and for ∆DEF, DE = 5 cm, EF = 7 cm, ∠E = 50°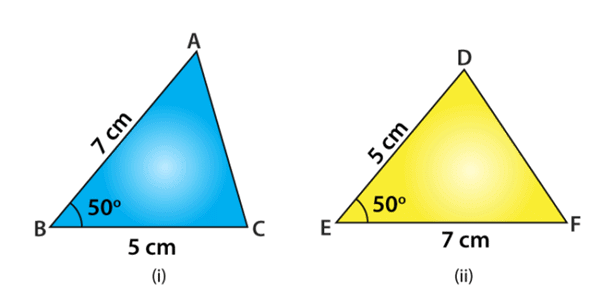
Solution:
Given: AB = EF = 7 cm,
BC = DE = 5 cm and
∠B =∠E = 50°
A↔F, B↔E, C↔D
By using SAS congruence rule, it can be written as
∆ABC ≅ ∆FED
ASA Congruence Rule (Angle – Side – Angle )
The triangles are said to be congruent if two angles and the included side of a triangle are equal to two corresponding angles and the included side of another triangle.
Example: Conclude that ∆AOC ≅ ∆BOD, using ASA congruence rule from the given figure.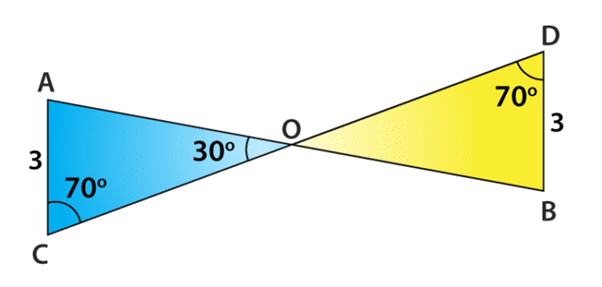
Solution:
Consider the two triangles AOC and BOD,
Given that ∠C = ∠D =70°
Also, note that ∠AOC = ∠BOD = 30° Which are vertically opposite angles
So, we can write that the angle A of triangle AOC
∆AOC = 180° – (70° + 30°) = 80° (By angle sum property of a triangle)
Similarly, for ∠B of ∆BOD = 180° – (70° + 30°) = 80°
So, we have ∠A = ∠B, AC = BD and ∠C = ∠D
Now, the side AC is between ∠A and ∠C and the side BD is between ∠B and ∠D.
So, by using ASA congruence rule, it is written as
∆AOC ≅ ∆BOD.
RHS Congruence Rule
The triangles are said to be congruent, then the hypotenuse and one side of a right-angled triangle are respectively equal to the hypotenuse and one side of another right-angled triangle.
Example: Some parts of two triangles measurements are given below. Using RHS congruence rule, examine whether the given two triangles are congruent or not. In case, if the triangles are congruent write the result in a symbolic form. For ∆ABC and ∆PQR, the measurements are given below. For triangle ABC, ∠B = 90°, AC = 8 cm, AB = 3 cm and triangle PQR, ∠P = 90°, PR = 3 cm, QR = 8 cm.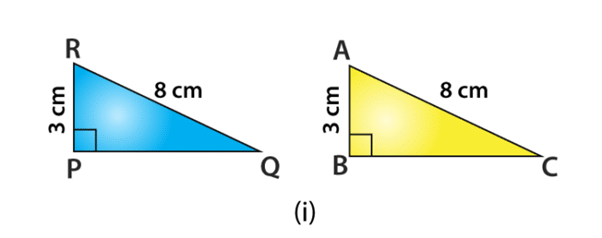
Solution:
Given : ∠B = ∠P = 90o,
Hypotenuse side AC = RQ = 8 cm and
side AB = RP = 3 cm
So, by RHS Congruence rule, the symbolic form of the congruent triangle is written as
∆ABC ≅ ∆RPQ
|
40 videos|471 docs|57 tests
|
FAQs on Congruence of Triangle - Mathematics (Maths) Class 9
| 1. What are congruent triangles? |  |
| 2. How can we prove triangles are congruent? |  |
| 3. Why is it important to study congruent triangles? |  |
| 4. Can two triangles be congruent if they have different sizes? |  |
| 5. Are all equilateral triangles congruent? |  |
















