Class 9 Math: Sample Question Paper- 7 (With Solutions) PDF Download
SECTION - A
Questions 1 to 20 carry 1 mark each.
Q.1. The total number of terms in the expansion of (a2 + 2ab + b2)101 is:
(a) 102
(b) 203
(c) 204
(d) None of these
Ans. (b)
We have, (a2 + 2ab + b2)101 = {(a + b)2}101 = (a + b)202
We know that the total number of terms in the expansion of (x + a)n is (n + 1).
∴ Total number of terms in the expansion of (a + b)202 is (202 + 1) = 203.
Total number of terms in the expansion of (a2 + 2ab + b2)101 is 203.
Q.2. What is the degree of the p(x) = 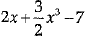
(a) 0
(b) 1
(c) 2
(d) 3
OR
Which of the following expressions is a polynomial?
(a) 5x2 - 4x + 3
(b) x + 2/x
(c) x1/2 - 3x + 2
(d) None of these
Ans. (d)
OR
(a)
Reason. 5x2 - 4x + 3 is a polynomial in x since I the exponent of x, in each term, is a non-negative integer
Q.3. If perpendicular distance of a point A from the x-axis is 6 units along the positive direction of the y-axis, then point A has:
(a) abscissa is 6 (b) ordinate is 6 (c) abscissa is - 6 (d) ordinate is-6
Ans. (b) ordinate is 6
Q.4. The two diagonals are equal in a
(a) parallelogram (b) rhombus (c) rectangle (d) trapezium
Ans. (c) A rectangle has equal diagonals.
Q.5. L is the foot of perpendicular from a point (5, 7, 10) on x-axis. The coordinates of L are
(a) ( 5 , 0 , 0 )
(b) (0,7,0)
(c) (0, 0, 10)
(d) None of these
Ans. (a) We know that on x-axis, y = 0 and z = 0. Therefore, the coordinates of foot of perpendicular L are (5, 0, 0).
Q.6. In ΔABC, AB = AC and ∠B = 50°. Then ∠C is equal to
(a) 40° (b) 50° (c) 80° (d) 130°
Ans. (b)
Given that AB = AC and ∠B = 50°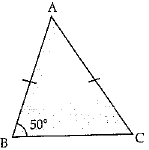
In ΔABC, AB = AC (given)
∠C = ∠B (angles opposite to equal sides are equal)
∠C = 500
Q.7. In given fig., ABCD is a parallelogram. If ar(ΔBFC) = 40 cm2 then ar(ΔAEB) is equal to: 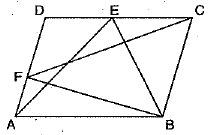
(a) 20 cm2
(b) 40 cm2
(c) 80 cm2
(d) 10 cm2
Ans. (b) 40 cm2
[∵ If a triangle and parallelogram are on the same base and between the same parallel, the area of the triangle is equal to half of the parallelograms.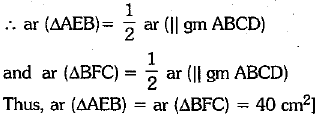
Q.8. Sum of interior angles of a pentagon is
(a) 360° (b) 450° (c) 540° (d) 180°
Ans. (c) Sum of interior angles of a pentagon
= (5 - 2) x 180° = 540°
Q.9. The three coordinate planes divide the space into number of parts equal to:
(a) 6
(b) 4
(c) 8
(d) 2
Ans. (c) The three coordinate planes divide the space into 8 parts (octants).
Q.10. A die is thrown 1000 times and the outcomes were recorded as follows :
If the die is thrown once more, then the probability that it shows 5 is:
(a) 9/50
(b) 3/40
(c) 4/25
(d) 7/25
OR
A coin is tossed 200 times. The head appears 79 times. The probability of a tail is
(a) 79/200
(b) 121/200
(c) 1
(d) 0
Ans. (b)
P (getting 5) = 150/1000 = 3/20
OR
(b)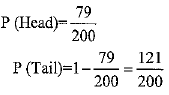
(Q.11 - Q.15) Fill in the blanks:
Q.11. If (x + 1) is a factor of p(x) = x98 + 2x37 + p, then the value of p is ......
Ans. 1
[∵ p(-l) = 0
⇒ (-1)98 + 2 (-1)37 + p = 0
⇒ 1 - 2 + p = 0
⇒ P = 1]
Q.12. The altitude of an equilateral ΔABC is ....... where a is the length of equal sides.
Ans. The altitude of an equilateral ΔABC is √3/2 x length of side.
Q.13. 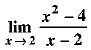 is equal to ____.
is equal to ____.
OR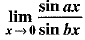 is equal to ____.
is equal to ____.
Ans. 4
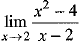
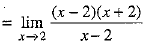
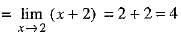
OR
a/b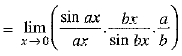
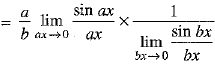
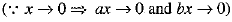
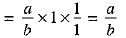
Q.14. In the given figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.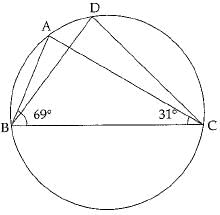
Ans. ∠BAC = 180°-(69°+ 31°)
= 80°
∠BDC =∠BAC = 80°
(Angles in same segment are equal)
Q.15. When we perform an experiment, it is called a ..........of the experiment.
Ans. trial
Q.16. If 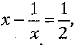 then write the value of
then write the value of 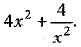
OR
Evaluate (0.2)3 - (0.3)3 + (0.1)3.
Ans. We have, 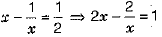
On squaring both sides, we get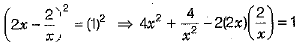
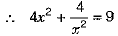
OR
Let a = 0.2, b = -0.3 and c = 0.1
Then, a + b + c = 0.2 - 0.3 + 0.1 = 0
We know that,
a3 + b3 + c3 = 3abc
∴ (0.2)3 + (- 0.3)3 + (0.1)3 = 3 x (0.2) x (-0.3) x (0.1)
= -0.018
Q.17. If A and B are two sets such that n(A) = 115; n(B) = 326, n(A - B ) = 47, then find n(A ∪ B).
Ans. Given, n(A) = 115, n(B) = 326, n(A - B) = 47
We know that n(A ∩ B) = n(A) - n(A - B) = 115 - 47 = 68
and n( A ∪ B) = n(A) + n(B) - n(A ∩ B) = 115 + 326 - 68 = 373
Q.18. In a parallelogram the diagonals are equal.
OR
An equilateral triangle is an acute angled triangle
Ans. False.
OR
True.
In an equilateral triangle, all the angles are 60°.
Q.19. The total surface area of a cube is 726 cm2. Find the length of its edge.
OR
If the volume of a cube is 3√3 a3, then find the total surface area of the cube.
Ans. Total surface area of a cube = 726 cm2
6 x (side)2 = 726
(side)2 = 121 = (11)2
side = 11
Hence, the length of the edge of cube is 11 cm.
OR
Let x be edge of a cube.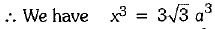
⇒ 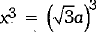
⇒ x = √3 a
Total surface area = 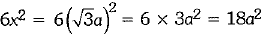
Q.20. Find the area of a triangle whose sides are 3 cm, 4 cm and 5 cm.
Ans. Let sides of a triangle are a = 3cm, b = 4cm and c = 5 cm.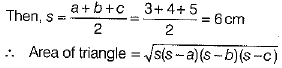
[by Heron’s formula]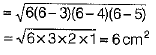
SECTION - B
Question numbers 21 to 26 carry 2 marks each.
Q.21. What is the value of 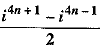 ?
?
Ans. 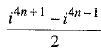
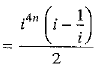
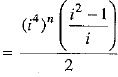
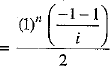
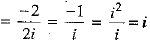
Q.22. Express 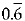 in the form of P/q where p and q are integers and q ≠ 0.
in the form of P/q where p and q are integers and q ≠ 0.
OR
Write the following in decimal form and say what kind of decimal expansion each has?
(i) 49/100 (ii) 2/5
Ans. Let,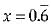
x = 0.6666.......... ...(i)
Multiplying by 10 on both the sides, we get,
10x = 6.6666 ...(ii)
From (ii) - (i), we get
9x = 6.0
Or, 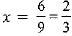
OR
(i) 49/100= 0.49, so it has terminating decimal expansion.
(ii) 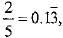 so it has no terminating decimal expansion.
so it has no terminating decimal expansion.
Q.23. Write Euclid’s fifth postulate. Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Ans. If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.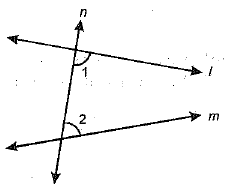
Yes.
Now, according to Euclid’s fifth postulate, when line ‘n’ falls on line 'l' and ‘m ’ such that ∠1 + ∠2 < 1800, then line l and line m on producing further will meet in the side of ∠1 and ∠2, which is less than 180°.
We find that the lines which are not according to Euclid’s fifth postulate i.e., ∠1 + ∠2 < 1800, do not intersect.
Q.24. Find the mean of the following distribution.
Ans. Table for mean distribution is given below.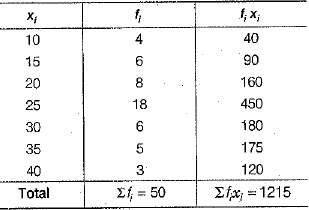
Here, 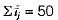
and 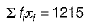
∴ 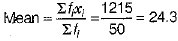
Q.25. If a card is drawn from a deck of 52 cards, then find the probability of getting a king or heart or a red card.
Ans. Out of 52 cards, one card can be drawn in 52C1 ways.
∴ Total number of elementary events = 52C1 = 52
There are 4 cards of king, 12 cards of hearts other than king and 12 cards of red colour other than heart and kings. Out of 28 cards, one card can be drawn in 28C1 ways.
∴ Favourable number of elementary events = 28C1 = 28
Required probability = 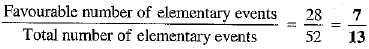
Q.26. Find the volume of a sphere whose surface area is 154 cm2.
OR
Find the length of the longest rod that can be placed in a room 12 cm long, 9 m broad and 8 m high.
Ans. Volume = 4/3 πr3
But surface area = 4πr3 =154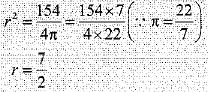
Volume = 539/3 or 179.67 cm3.
SECTION - C
Question 27 to 34 carry 3 marks each.
Q.27. Calculate mean and mean deviation about median for the following data:
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Frequency | 6 | 7 | 15 | 16 | 4 | 2 |
Or
A committee of two persons is selected from two men and two women. What is the probability that the committee will have (a) no man? (b) one man? (c) two men?
Ans. Calculation of mean deviation from median:
Here, N= 50.
∴ N/2 = 50/2 = 25, so median class is 20 - 30.
From the table: l = 20, h= 10, f= 15, cf= 13
Using the formula: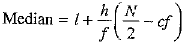
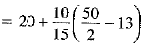
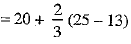
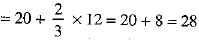
Thus, mean deviation about median
= M.D. (Median)
Calculation of Mean: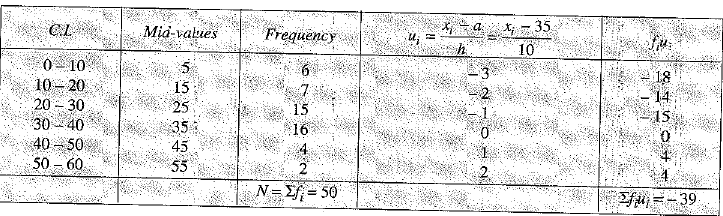
Let the assumed mean a = 35
∴ Mean is given by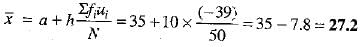
OR
The total number of persons = 2 men + 2 women = 4
Out of these four persons, two persons can be selected in 4C2 ways.
(a) No man in the committee of two persons
= There will be two women in the commits
Out of 2 women, two can be selected in 2C2 ways.
∴ 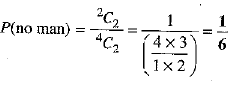
(b) One man in the committee of two persons means that there is one man and one woman in the committee.
One man out of 2 men can be selected in 2C1 ways and 1 woman out of 2 women can be selected in 2C1 ways. Together they can be selected in 2C1 x 2C1 ways.
∴ 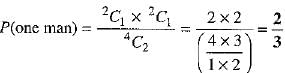
(c) Two men can be selected out of 2 men in 2C2 way.
∴ 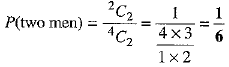
Q.28. Factorize 2x2 + 3√5 x + 5.
OR
Factorize x3 - 2x2 - x + 2
Ans. 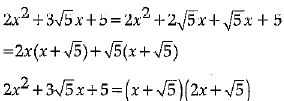
OR
x3 - 2x2 - x + 2
= x2(x - 2) -1(x - 2) [∴ a2 - b2 = (a - b)(a + b)]
= (x -2 )(x2- 1)
= (x - 2)(x - 1)(x + 1)
Q.29. If two circles intersect in two points, prove that the line through their centres is the perpendicular bisector of the common chord.
OR
Two chords PQ and QR of a circle are equal. Prove that the centre of the circle lies on the angle bisector of ∠PQR.
Ans. Given: Two circles C(0, r) and C (O', s) Intersect at P and Q.
To Prove: OO' is perpendicular bisector of the chord PQ.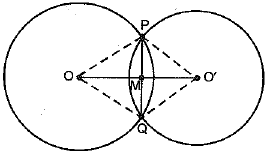
Const. : Join OP, OQ, O'P and O'Q
Proof: In ΔOPO' and ΔOQO'
OP = OQ [radii of same circle]
O'P = O'Q [radii of same circle]
OO' = OO' [common]
⇒ ΔOPO' = ΔOQO' [by SSS congruence axiom]
⇒ ∠POM = ∠QOM [c.p.c.t,]
Now, in ΔPOM and ΔQOM
OP = OQ [radii of same circle]
∠POM = ∠QOM [proved above]
OM = OM [common]
⇒ ΔPOM ≅ ΔQOM [by SAS congruence axiom]
PM = QM and
∠PMO = ∠QMO [c.p.c.t.]
Also, ∠PMO + ∠QMO'= 180° [a linear pair]
⇒ ∠PMO = ∠QMO
= 90°
Hence, OO' is the perpendicular bisector of the chord PQ.
OR
Given: Two equal chords PQ and QR of a circle C(O, r).
To Prove: Centre O of the circle lies on the bisector of ∠PQR.
Const. : Join PR, draw bisector QX of ∠PQR and let it intersects PR in M.
Proof: In ΔPQM and ΔRQM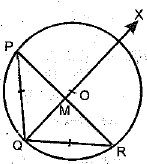
PQ = RQ [given]
∠PQM = ∠RQM [by construction]
QM = QM [common]
⇒ ΔPQM = ΔRQM [by SAS congruence axiom]
⇒ PM = RM
and ∠PMQ = ∠RMQ [c.p.c.t.]
But ∠PMQ + ∠RMQ = 1800 [a linear pair]
⇒ ∠PMQ = ∠RMQ = 90°
⇒ QM is the perpendicular bisector of chord PR.
⇒ QM passes through the centre O.
[∵ perpendicular bisector of a chord always passes through the centre]
Hence, the centre of the circle lies on the angle bisector of ∠PQR.
Q.30. In the given figure, side BC of ΔABC is produced to form ray BD and CE || BA. Show that ∠ACD = ∠A + ∠B. Deduce that ∠A + ∠B + ∠C = 180°.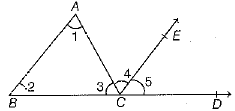
Ans. Given. CE || BA, AC and BC are the transversal.
∴ ∠4 = ∠1 ...(i) [alternate interior angles]
and ∠5 = ∠2 ...(ii) [corresponding angles]
On adding Eqs. (i) and (ii), we get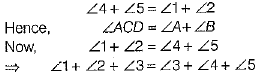
[adding ∠3 both sides]
∴ 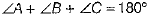
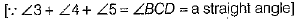
Hence proved.
Q.31. Write the number z = 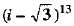 3 in algebraic form.
3 in algebraic form.
OR
Find the square root of - 7 - 24i.
Ans. We have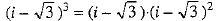
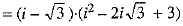
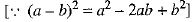
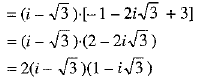
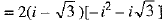
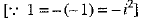
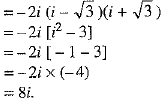
Now,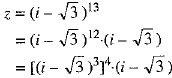
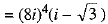
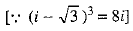
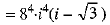
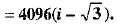
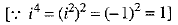
OR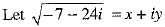 ...(1)
...(1)
Squaring both sides, we have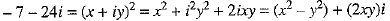
Comparing real and imaginary parts on both sides, we have
x2 - y2 = - 7 ...(2)
and 2xy = - 24 ⇒ 4x2y2 = 576 ...(3)
Now, (x2 + y2)2 = (x2 - y2)2 + 4x2y2 = (-7)2 + 576 = 49 + 576 = 625 [using (2) and (3)]
Taking square roots of both sides, we have
x2 + y2 = 25 ...(4) [∵ Sum of squares of real numbers cannot be negative]
Adding and subtracting (2) and (4), we get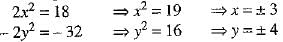
Since xy < 0, therefore x and y are of opposite sign.
∴ x = 3, y = -4 or x = -3, y = 4
Putting the values of x and y in (1), we get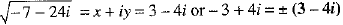
Q.32. Prove that the diagonals of a rectangle are equal in length.
Ans.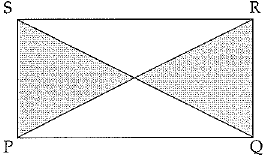
Let PQRS be a rectangle
In ΔSPQ and ΔRQP,
SP = RQ. (Opp. Sides of rectangle are equal)
∠SPQ = ∠RQP = 90°
(Each angle of rectangle is right angle)
PQ = QP (common)
∴ 
Q.33. Three vertices (corners) of a rectangle are A (1, 3), B (1, -1) and C (7, -1). Plot these points on a graph paper and hence use it to find the coordinates of the fourth vertex. Also, find the area of the rectangle as well as the point of intersection of diagonal from graph.
Ans. Plot the points A (1, 3 ), B (1, -1) and C (7, -1) on the graph paper. Join the points to complete the rectangle ABCD. Now, read the coordinates of the point D from the graph paper. Clearly, point D from the graph is (7, 3). From graph,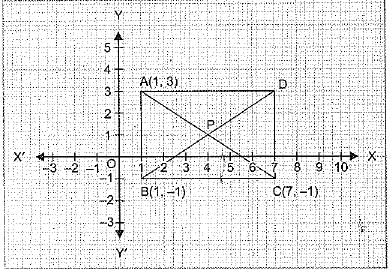
Length of rectangle = 6 units
Breadth of rectangle = 4 units
Area of rectangle = 6 x 4 = 24 sq. units
Now, point of intersection of diagonals is P(4, 1).
Q.34. An umbrella is made by stitching 8 triangular pieces of cloth of two different colours. Each piece measuring 20 cm, 40 cm and 40 cm. How much cloth of each colour is required for the umbrella?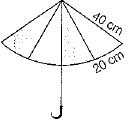
OR
The slant height and base diameter of a conical tomb are 25 m and 14 m, respectively. Find the cost of white-washing its curved surface area at the rate of ₹210 per 100 m2?
Ans. Here, each triangular piece is an isosceles triangle with sides a = 40 cm, b = 40 cm and c = 20 cm.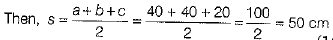
Area of each triangular piece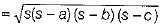
[by Heron’s formula]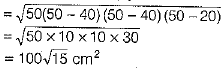
Now, there are 4 triangular pieces of one colour and 4 triangular pieces of other colour.
Hence, total area of cloth of each colour.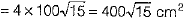
OR
Given, diameter of conical tomb = 14 m
and slant height of conical tomb (l) = 25 m
SECTION - D
Questions 35 to 40 carry 4 marks each
Q.35. If 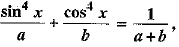 prove that:
prove that: 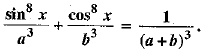
OR
Prove that: cos2A + cos2 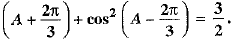
Ans. We have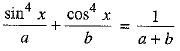
⇒ 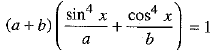
⇒ 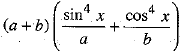
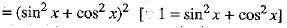
⇒ 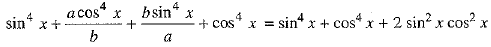
⇒ 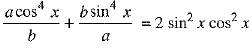
⇒ 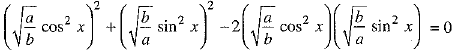
⇒ 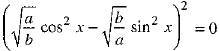
⇒ 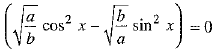
⇒ 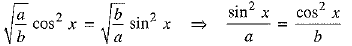
⇒ 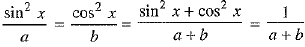
⇒ 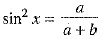 ...(i)
...(i)
and 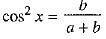 ...(ii)
...(ii)
Now, 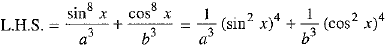
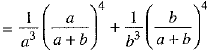 [using (i) and (ii)]
[using (i) and (ii)]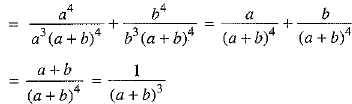
= R.H.S.
OR
We know that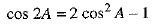
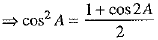
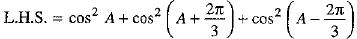
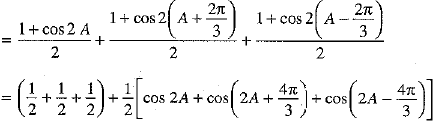
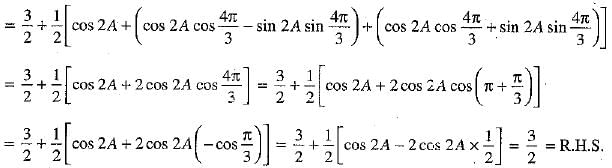
Q.36. Evaluate: 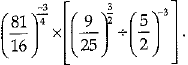
Ans.
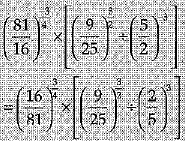
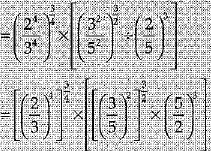
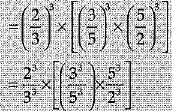
= 1
Q.37. Draw a histogram of the weekly expenses of 125 students of a school given below:
Ans. Here, the class sizes are different, so calculate the adjusted frequency for each class by using the formula.
Frequency density or adjusted frequency for a class = 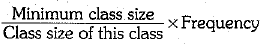
Here, the minimum class size = 10 - 0 = 10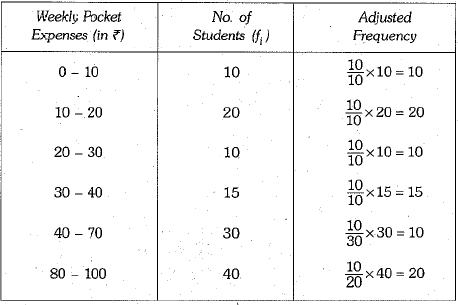
Let us represent weekly pocket money along x-axis and corresponding adjusted frequencies along y-axis on a suitable scale, the required histogram is as given below: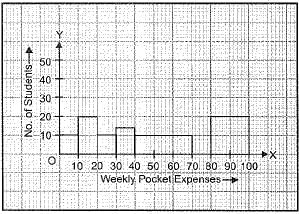
Q.38. Construct a ΔABC in which BC = 4.6 cm, ∠B = 45° and AB + CA = 8.2 cm.
Ans. Given, BC = 4.6 cm, ∠B = 45° and AB + CA = 8.2 cm
In horizontal axis, take 1 block is equal to 10 units and in vertical axis, take 1 block is equal to 5 units.
Steps of construction
(i) Draw the base line segment BC = 4.6 cm.
(ii) At the point B, make ∠XBC = 45°.
(iii) Now, cut a line segment BD equal to AB + AC= 8.2 cm from the ray BX.
(iv) Join DC.
(v) Draw perpendicular bisector MN of CD which meets BX at A.
(vi) On joining AC, we net the required ΔARC.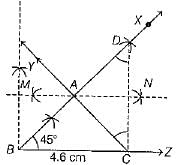
Q.39. Between 1 and 31, m numbers have been inserted in such a way that the resulting sequence is an A,P, and the ratio of 7th and (m - 1)th numbers is 5 : 9. Find the value of m.
OR
If p,q,r are in G.P. and the equations px2 + 2qx + r = 0 and dx2 + 2ex + f = 0 have a common root, then show that 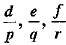 are in A.P.
are in A.P.
Ans. Let A1, A2,...., Am be m numbers between 1 and 31 such that 1 ,A1, A2,....,Am, 31 is an A.P.
Here, 31 is the (m + 2)th term. i.e..
31 = 1 + [(m+2) - 1]d
⇒ 31 = 1 + (m + 1)d
⇒ 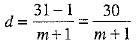
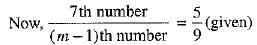
⇒ 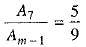
⇒ 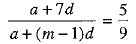
⇒ 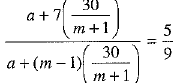
⇒ 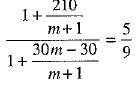 [∵ a = 1]
[∵ a = 1]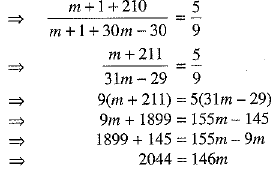
⇒ 14 = m
Hence, the value of m is 14.
OR
Since, p, q, r are in G.P., therefore
q2 = pr ...(i)
The roots of the given equation
px2 + 2qx + r = 0
are given by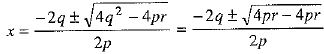 [using (1)]
[using (1)]
⇒ 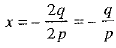 ...(2)
...(2)
From (2), it is clear that both the roots of equation px2 + 2qx + r = 0 are equal, i.e., x = -q/p.
It is given that the equations px2 + 2qx + r = 0 and dx2 + 2ex + f = 0 have a common root.
∴ 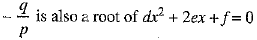
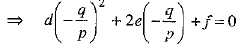
⇒ dq2 - lepq + fp2 = 0
⇒ dpr - lepq + fp2 = 0 [using (1)]
⇒ p[dr - 2eq +fp]= 0
⇒ dr - 2eq +fp = 0 [∵ p ≠ 0]
⇒ 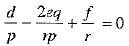 [Dividing both sides by pr]
[Dividing both sides by pr]
⇒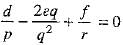 [using (1)]
[using (1)]
⇒ 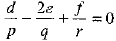
⇒ 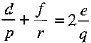
⇒ 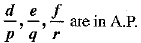
Q.40. The points scored by a basketball team in a series of 16 matches are as follows. Find the median and mode of data:
17,2, 7,27, 5,14,18,10,24,25,48,10,8, 7,10,28,25. Find median and mode of the series.
OR
Find the mean salary of 60 workers of a factory from the following table.
| Salary (Rs.) | No. of Workers |
| 3000 | 16 |
| 4000 | 12 |
| 5000 | 10 |
| 6000 | 8 |
| 7000 | 6 |
| 8000 | 4 |
| 9000 | 3 |
| 10000 | 1 |
| TOTAL | 60 |
Ans. Arrange the data in ascending order.
2, 5, 7, 7, 8, 10, 10, 10, 14, 17, 18, 24, 25, 27, 28, 48
N = 16, which in even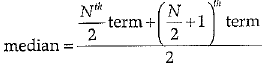
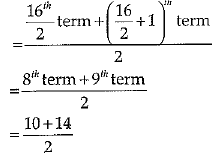
median = 12
Mode = The most frequently occurring observation
= 10 i.e., 3 times occurring 10
∴ Mode = 10
OR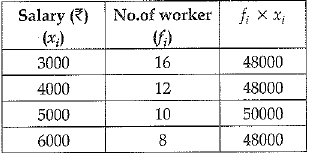
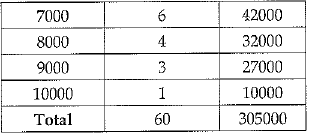
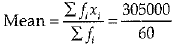
= 5083.33
∴ Mean salary of 60 workers = ₹ 5083.33
FAQs on Class 9 Math: Sample Question Paper- 7 (With Solutions)
| 1. What is the format of the Class 9 Math Sample Question Paper- 7? |  |
| 2. Are the solutions provided for the Sample Question Paper- 7 of Class 9 Math? |  |
| 3. How can students benefit from practicing the Sample Question Paper- 7 of Class 9 Math? |  |
| 4. Can the Sample Question Paper- 7 of Class 9 Math be used for self-study? |  |
| 5. How should students utilize the solutions provided for the Sample Question Paper- 7 of Class 9 Math? |  |



















