Ex-21.2 (Part - 1), Surface Area And Volume Of Sphere, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1. Find the volume of a sphere whose radius is : (i) 2 cm (ii) 3.5 cm (iii) 10.5 cm.
Sol.
(i) Radius(r) = 2cm
Therefore volume = 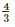 πr3
πr3
= 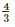 ×
×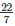 ×(2)3
×(2)3
= 33.52cm3
(ii) Radius(r) = 3.5cm
Therefore volume = 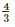 πr3
πr3
= 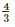 ×
×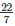 ×(3.5)3 = 179.666cm3
×(3.5)3 = 179.666cm3
(iii) Radius(r) = 10.5cm
Therefore volume = 43πr3
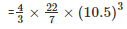 = 4851cm3
= 4851cm3
Q2. Find the volume of a sphere whose diameter is : (i) 14 cm (ii) 3.5 dm (iii) 2.1 m
Sol.
(i) Diameter = 14cm, Radius(r) = 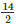 = 7cm
= 7cm
Therefore volume = 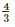 πr3
πr3
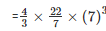 = 1437.33cm3
= 1437.33cm3
(ii) Diameter = 3.5dm, Radius(r) = 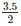 = 1.75dm
= 1.75dm
Therefore volume = 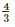 πr3
πr3
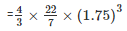
= 22.46dm3
(iii) Diameter = 2.1m, Radius(r) = 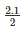 = 1.05m
= 1.05m
Therefore volume = 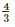 πr3
πr3
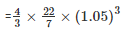 = 4.851m3
= 4.851m3
Q3. A hemispherical tank has the inner radius of 2.8 m. Find its capacity in liters.
Sol.
Radius of the tank = 2.8m
Therefore Capacity = 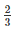 πr3
πr3
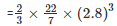 = 45.994m3
= 45.994m3
1m3 = 1000l
Therefore capacity in litres = 45994 litres
Q4. A hemispherical bowl is made of steel 0.25 cm thick. The inside radius of the bowl is 5 cm. Find the volume of steel used in making the bowl.
Sol.
Inner radius = 5cm
Outer radius = 5 + 0.25 = 5.25
Volume of steel used = Outer volume - Inner volume
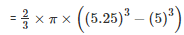
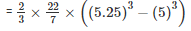
= 41.282cm3
Q5. How many bullets can be made out of a cube of lead, whose edge measures 22 cm, each bullet being 2 cm in diameter?
Sol.
Cube edge = 22cm
Therefore volume of the cube = (22)3 = 10648cm3
And,
Volume of each bullet = 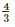 πr3 =
πr3 = 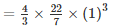
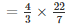
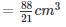
Number of bullets = 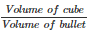
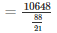 = 2541
= 2541
Q6. A shopkeeper has one laddoo of radius 5 cm. With the same material, how many laddoos of radius 2.5 cm can be made?
Sol.
Volume of laddoo having radius = 5cm
i.e Volume(V1) = 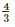 πr3
πr3
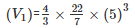
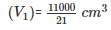
Also Volume of laddoo having radius 2.5cm
i.e Volume(V2) = 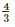 πr3
πr3
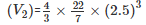
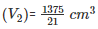
Therefore number of laddoos = 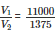 = 8
= 8
Q7. A spherical ball of lead 3 cm in diameter is melted and recast into three spherical balls. If the diameters of two balls be 32cm and 2 cm, find the diameter of the third ball.
Sol.
Volume of lead ball = 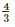 πr3
πr3
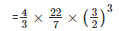
Diameter of first balld1 = 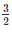 cm
cm
Radius of first ball r1 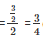 cm
cm
Diameter of second ball d2 = 2cm
Radius of second ball r2 = 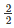 cm = 1cm
cm = 1cm
Diameter of third balld3 = d
Radius of third ball r3 = 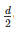 cm
cm
Volume of lead ball = 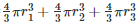
Volume of lead ball = 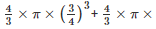
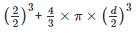
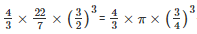
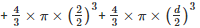
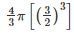
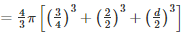
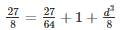
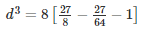
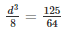
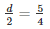
d = 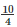
d = 2.5cm
Q8. A sphere of radius 5 cm is immersed in water filled in a cylinder, the level of water rises 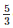 cm. Find the radius of the cylinder.
cm. Find the radius of the cylinder.
Sol.
Radius of cylinder = r
Radius of sphere = 5cm
Volume of sphere = 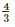 πr3
πr3
= 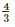 ×π×(5)3
×π×(5)3
Height of water rised = 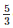 cm
cm
Volume of water rised in cylinder = πr2h
Therefore, Volume of water rises in cylinder = Volume of sphere
Let r be the radius of the cylinder
πr2h = 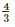 πr3
πr3
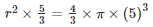
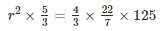
r2 = 20×5
r = 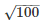
r = 10cm
Q9. If the radius of a sphere is doubled, what is the ratio of the volume of the first sphere to that of the second sphere?
Sol.
Let v1 and v2 be the volumes of the first and second sphere respectively
Radius of the first sphere = r
Radius of the second sphere = 2r
Therefore, 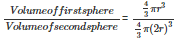
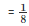
Q10. A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
Sol.
Given that
Volume of the cone = Volume of the hemisphere
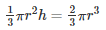
r2h = 2r3
h = 2r
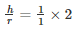 = 2
= 2
Therefore
Ratio of their heights = 2 : 1
Q11. A vessel in the form of a hemispherical bowl is full of water. Its contents are emptied in a right circular cylinder. The internal radii of the bowl and the cylinder are 3.5 cm and 7 cm respectively. Find the height to which the water will rise in the cylinder.
Sol.
Given that
Volume of water in the hemispherical bowl = Volume of water in the cylinder
Let h be the height to which water rises in the cylinder
Inner radii of the bowl = r1 = 3.5cm
Inner radii of the bowl = r2 = 7cm
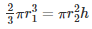
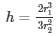
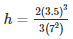
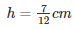
Q12. A cylinder whose height is two thirds of its diameter has the same volume as a sphere of radius 4 cm. Calculate the radius of the base of the cylinder.
Sol.
Given that
Height of the cylinder = 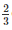 diameter
diameter
We know that
Diameter = 2(radius)
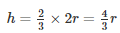
Volume of the cylinder = Volume of the sphere
πr2h = 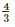 πr3
πr3
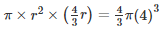
(r)3 = (4)3
r = 4cm
Q13. A vessel in the form of a hemispherical bowl is full of water. The contents are emptied into a cylinder. The internal radii of the bowl and cylinder are respectively 6 cm and 4 cm. Find the height of water in the cylinder.
Sol.
It is given that
Volume of water in hemispherical bowl = Volume of cylinder
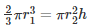
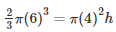
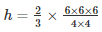
h = 9cm
Q14. A cylindrical tub of radius 16 cm contains water to a depth of 30 cm. A spherical iron ball is dropped into the tub and thus level of water is raised by 9 cm. What is the radius of the ball?
Sol.
Let r be the radius of the iron ball
Radius of the cylinder = 16cm
Then,
Volume of iron ball = Volume of water raised in the hub
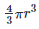 = πr2h
= πr2h
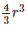 = (16)2×9
= (16)2×9
r3 =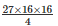
r3 = 1728
r = 12cm
Therefore radius of the ball = 12cm.
Q15. A cylinder of radius 12 cm contains water to a depth of 20 cm. A spherical iron ball is dropped into the cylinder and thus the level of water is raised by 6.75 cm. Find the radius of the ball. (Use = 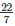 ).
).
Sol.
Given that :
Radius of the cylinder = 12cm = r1
Raised in raised = 6.75 cm = r2
Volume of water raised = Volume of the sphere
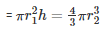
= 12×12×6.75 = 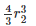
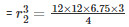
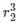 = 729
= 729
= r2 = 9cm
Radius of the sphere is 9cm
Q16. The diameter of a copper sphere is 18 cm. The sphere is melted and is drawn into a long wire of uniform circular cross - section. If the length of the wire is 108 m, find its diameter.
Sol.
Given that diameter of a copper sphere = 18cm
Radius of the sphere = 9cm
Length of the wire = 108m = 10800cm
Volume of cylinder = Volume of sphere
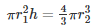
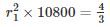 ×9×9×9
×9×9×9
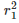 = 0.009
= 0.009
r1 = 0.3cm
Therefore Diameter = 2×0.3 = 0.6cm
FAQs on Ex-21.2 (Part - 1), Surface Area And Volume Of Sphere, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the formula for calculating the surface area of a sphere? |  |
| 2. How do you find the volume of a sphere? |  |
| 3. What is the difference between the surface area and volume of a sphere? |  |
| 4. Can the surface area of a sphere be greater than its volume? |  |
| 5. How can the surface area and volume of a sphere be useful in real-life applications? |  |





















