Class 9 Math: Sample Question Paper- 11 (With Solutions) PDF Download
SECTION - A
Question numbers 1 to 20 carry 1 mark each.
Q.1. If A and B are any two events having 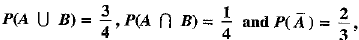 then
then 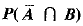 is
is
(a) 1/2
(b) 1/4
(c) 1/12
(d) 5/12
Ans. Choice (d) is correct.
∵ 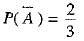
⇒ 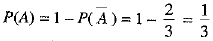
We know that, P(A ∪ B) = P(A) + P(B) - P(A ∩ B)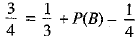
⇒ 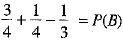
⇒ 2/3 = P(B) ...(1)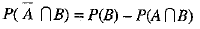
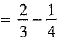 [using (1)]
[using (1)]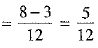
Q.2. The coefficient of x2 in (3x2 - 5) (4 + 4x2)
(a) 12
(b) 5
(c) -8
(d ) 9
OR
If a + b + c = 0, then factor of the expression [(a + b)3 + (b + c)3 + (c + a)3] is:
(a) abc
(b) a + b + c
(c) ab + be + ca
(d) (a + b)
Ans. (c) (3x2 - 5) (4 + 4x2) = 12x2 + 12x4 - 20 - 20x2
= 12x4 - 8x2 - 20
Co-efficient of x2 = - 8
OR
(d) (a + b) + (b + c) + (c + a)
= 2 (a + b + c)
= 0 (∵ a + b + c = 0)
∴ (a + b)3 + (b + c)3 + (c + a)3 = 3 (a + b) +(b + c) + (c + a)
⇒ (a + b) is a factor.
Q.3. The distance of a point (0, -6) from the origin is:
(a) -6 units (b) 0 units (c) 6 units (d) cannot be determined
Ans. (c) 6 units
Q.4. In the given figure, if bisector of ∠A divides BC in the ratio 1:1 and ∠D = 90°. Then, ΔABC is of the type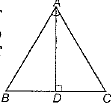
(a) a right angled triangle
(b) an isosceles triangle
(c) an equilateral triangle
(d) None of the above
Ans. (b) In ΔADB and ΔADC,
BD = DC [since, AD divides SC]
∠ADB = ∠ADC [each 90°]
AD = AD [common]
∴ ΔADB ≌ ΔADC [by SAS criterion]
⇒ AB = AC [by CPCT]
∴ ΔABC is an isosceles triangle.
Q.5. In a distribution, if variance is 9, then standard deviation is
(a) 3
(b)- 3
(c) ± 3
(d) 0
Ans. Choice (a) is correct.
3 as standard deviation = 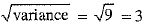
Q.6. The radius of a sphere is 4r, and then its volume will be
(a) 4πr3/3
(b) 4πr3
(c) 8πr3/3
(d) 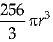
Ans. (d)
Volume of the sphere =4/3 πR3
But radius R = 4r
Therefore, volume of the sphere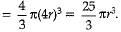
Q.7. In the given figure p||q, T is the mid-point of QR, if ar (ΔPQR) = x ar(ΔPST), then value of x is: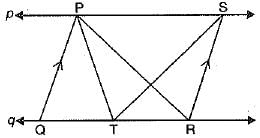
(a) 1
(b) 1/4
(c) 2
(d) 1/2
Ans. (a) 1
[∵ Clearly, ΔPQR and parallelogram PQRS are on the same base QR and between same parallel lines p and q.
∴ 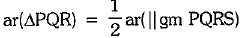
Similarly, 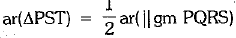
Thus, ar(ΔPQR) = ar(ΔPST)
Hence, x = 1]
Q.8. The number of triangles that can be drawn having its angles as 53°, 64° and 63°, is/are
(a) one
(b) two
(c) infinitely
(d) None of these
Ans. (c) Infinitely many triangles, because sum of all interior angles of every triangle is always 180°.
Q.9. If y = sin a cos x, then dy/dx is
(a) cos x sin a + sin x cos a
(b) cos a sin x
(c) - sin a sin x
(d) - sin x cos a
Ans. Choice (c) is correct.
∵ y = sin a cos x 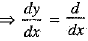 (sin a cos x) = sin a d/dx (cos x) = sin a(- sin x) = - sin a sin x
(sin a cos x) = sin a d/dx (cos x) = sin a(- sin x) = - sin a sin x
Q.10. ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140°, then ∠BAC is equal to
(a) 80°
(b) 50°
(c) 40°
(d) 30°
Ans. (b)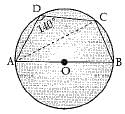
∠ACB = 90° (Angle in a semi circle)
∠CBA = 180° - 140°
= 40°
(opposite angles of cyclic quadrilateral)
Also, 90° + 40° + ∠BAC = 180°
∠BAC = 180 -130 = 50°
Q.11. If g(x) = 4x2 - 10x + 4, then value to g(2) = ...........
Ans. g(x) = 4x2 - 10x + 4
Put
x = 2, then
g(2) = 4(2)2 - 10 x 2 + 4
= 4 x 4 - 20 + 4
= 16 - 20 + 4 = 20 - 20 = 0
Q.12. If a, b and c are sides of a triangle and a2 + b2 + c2 = bc + ca + ab, then the triangle is .............
Ans. Given, a2 + b2 + c2 = bc + ca + ab
⇒ a2 + b2 + c2 - bc - ca - ab = 0
⇒ 1/2 (2a2 + 2b2 + 2c2 - 2bc - 2ca - 2ab) = 0
⇒ 1/2 {(a - b)2 + (b - c)2 + {c - a)2} = 0
⇒ a - b= 0, b - c = 0, c - a = 0
⇒ a = b = c
Hence, the triangle is ecuilateral triangle.
Q.13. The component statements of the compound statement “125 is a multiple of 7 or 8” are (i) ___________and (ii)___________ .
Ans. (i) 125 is a multiple of 7 (ii) 125 is a multiple of 8
The component statements are (i) 125 is a multiple of 7 (ii) 125 is a multiple of 8
Q.14. The semi-perimeter of a equilateral triangle is 45 cm, find the area of equilateral triangle.
Ans.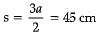
⇒ a = 30 cm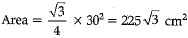
Q.15. Write any two solutions of the linear equation 4x + 3y = 12.
Ans. (0, 4) ; (3, 0)
Q.16. If (x + a) is a common factor of ( x2 + px + q) and (x2 + lx + m), then find the value of a.
OR
What will be the values of a and b, so that the polynomial x3 + 10x2 + ax + b is exactly divisible by x -1 as well as x - 2?
Ans. Let f(x) = x2 + px + q and g(x) = x2 + lx + m If (x + a) is a common factor of f (x) and g(x), then f(-a) = 0 and g(-a) = 0
⇒ (-a)2 + p(-a) + q = 0
⇒ a2 - pa + q = 0 ...(i)
Also, a2 - la + m = 0 ...(ii)
On subtracting Eq. (ii) from Eq. (i), we get
(l - p)a + q - m = 0 ⇒ (l - p)a = m - q
∴ 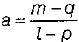
OR
(x-1) and (x-2)are factors of given polynomial.
We have,
1 + 10 + a + b = 0 [by factor theorem]
⇒ a + b = -11... (i)
and 8 + 40 + 2a + b = 0
48 + 2a + b = 0 ⇒ 2a + b = -48 ...(ii)
From Eqs. (i) and (ii), we get
a = -37 and b = 26
Q.17. Write the contrapositive of the following statement:
If a number is divisible by 9, then it is divisible by 3.
Ans. We know that the contrapositive of the statement
“If p, then q" is “If ~ q, then ~ p"
If a number is not divisible by 3, it is not divisible by 9.
Q.18. Area of triangle with sides 4 cm, 5 cm and 6 cm is 15 square units
Ans. False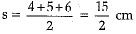
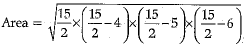
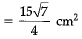
Q.19. Find the coefficient of x2 in the product (3x2 -5) (4 + 4x2).
Ans. Here, (3x2 - 5) (4 + 4x2)
= 12x2 + 12x4 - 20 - 20x2
12x4 - 8x2 - 20
Clearly, coefficient of x2 is - 8.
Q.20. The sides of a triangle are x, x + 1, 2x - 1 and its area is x√10. What is the value of x?
Ans. Given, sides of a triangle are x, x + 1, 2x - 1 and its area = x√1o
Let a = x, b = x + 1, c = 2x - 1
∴ 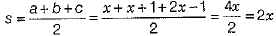
Area of triangle = 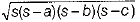 [ by Heron's formula]
[ by Heron's formula]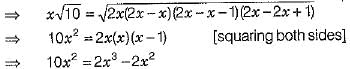
⇒ 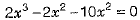
⇒ 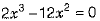
⇒ 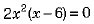
⇒ 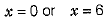
∵ x = 0 is not possible, because side cannot be zero, we get, x = 6
SECTION - B
Question number 21 to 26, carry 2 marks each.
Q.21. Let A = {1, 3} and B = {2, 3, 4}. Find the number of relations from A to B.
OR
Let A = {1, 2, 4, 5}, B = {2, 3, 5, 6}, C = {4, 5, 6, 7} verify the identity: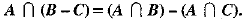
Ans. Here, n(A) = 2 and n(B) = 3
∴ n(A x B) = n(A) x n(B) = 2 x 3 = 6
Number of subsets of A x B
= 26
= 64
We know that every subset of A x B is a relation from A to B.
Hence, there are in all 64 relations from A to B.
OR
Given, A = {1, 2, 4, 5}, B = (2, 3, 5, 6} and C = {4, 5, 6, 7}
B - C = (2, 3, 5, 6} - {4, 5, 6, 7} = {2, 3}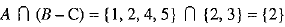 ...(i)
...(i)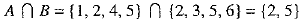
and 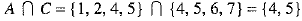
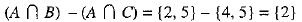 ...(2)
...(2)
From (1) and (2), we have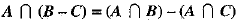
Q.22. In the given figure AC = DC, CB = CE, show that AB = DE.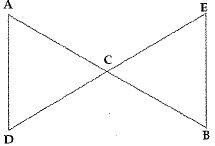
Write Euclid's axiom to support this.
Ans. AC = DC (Given)
CB = CE
[Using Euclid's 2nd axiom; "If equals are added to equals, the wholes are equal."]
Adding, AC + CB = DC + CE
AB = DE [Hence proved]
Q.23. In the figure, we have X and Y are the mid-points of AC and BC and AX = CY. Show that AC = BC.
Ans. Here, X and Y are the mid-points of AC and BC.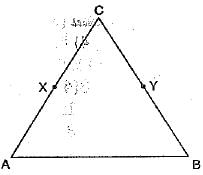
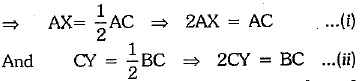
Also, AX = CY [given]
⇒ 2AX = 2CY ...(iii)
[∵ Euclid’s sixth axioms says, things which are double of the same thing are equal to one another]
From (i), (ii) and (iii), we have
AC = BC
Q.24. Charity is the act of giving help to needy persons. It is a humanitarian act. It involves giving money, goods or time and effort to those who need it. It is done without expecting something in return. In this order, Kishan buys x kg apples at the rate of INR 80 and INR 40 per kg for charity. Along that, he sells 10 kg pomegranate at the rate of INR 120 per kg. While the quantity of oranges is equal to the square of the apple quantity.
(i) Write an equation of the total cost of the quantity.
(ii) Write an equation of the total quantity.
(iii) Find the degree of an equation of total cost of quantity.
(iv) Kishan thinks that he will buys 5 kg apples for INR 2600. Is Kisharis assumption correct?
Ans. (i) According to the question, an equation of the total cost of quantity in terms of x is
p(x) = 80x + 40x2 + 10 x 120
= 80x + 40x2 +1200
(ii) An equation of the total quantity in terms of x is
g(x) = x + x2 + 10
(iii) The degree of p(x) is 2.
(iv) Here, x = 5
∴ p(5) = 80 x 5 + 40 x (5)2 + 1200
= 400 + 1000 + 1200
= INR 2600
Hence, Kishan buys 5 kg apples at INR 2600.
Q.25. If 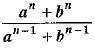 is the A.M. between a and b then find the value of n.
is the A.M. between a and b then find the value of n.
OR
Find the sum of the series:
2 + 6 + 18 + .... + 486
Ans. We know that A.M. between a and b is a+b/2.
According to question, we have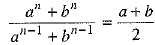
⇒ 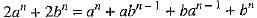
⇒ 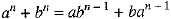
⇒ 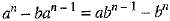
⇒ 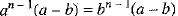
⇒ 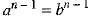 [∵ a ≠ b]
[∵ a ≠ b]
⇒ 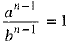
⇒ 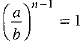
⇒ 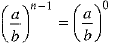 [a0 = 1, a ≠ 0]
[a0 = 1, a ≠ 0]
⇒ n - 1 = 0
⇒ n = 1
OR
Here, a = 2, r = 6/2 = 3 and arn - 1 = 486 (last term)
∴ Required sum = 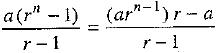
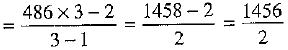
= 728
Q.26. Find the mean of the first ten prime numbers.
Ans. The first 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
Their mean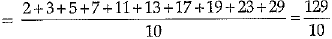
= 12.9
SECTION - C
Question 27 to 34, carry 3 marks each
Q.27. If 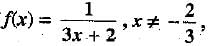 , then show that
, then show that 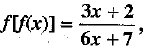 provided that x ≠ -7/6.
provided that x ≠ -7/6.
Ans. We have f(x) = 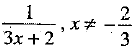
Then, 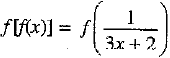
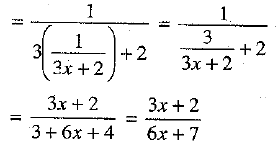
Clearly, 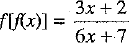 is real for 6x + 7 ≠ 0, i.e.,f[f(x)] is defined for 6x + 7 ≠ 0, i.e., x ≠ -7/6.
is real for 6x + 7 ≠ 0, i.e.,f[f(x)] is defined for 6x + 7 ≠ 0, i.e., x ≠ -7/6.
Hence, 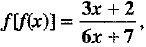 provided that x ≠ -7/6.
provided that x ≠ -7/6.
Q.28. Draw a triangle whose sides are represented by x = 0, y = 0 and x + y = 3 in the Cartesian system. Also, find the coordinates of its vertices.
Ans. Given, x + y = 3
On the y-axis put x = 0 then
y = 3
Hence on the y-axis co-ordinate of B is (0, 3) On the x-axis put y = 0 then
x = 3
Hence on the x-axis co-ordinate of A is (3, 0)
Hence a triangle whose sides are x = 0, y = 0, and x + y = 3 is as shown in fig.
Again the vertices of triangle are A (3, 0), B (0, 3) and O (0, 0).
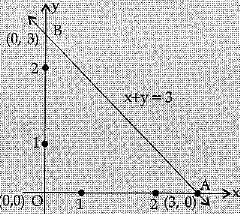
Q.29. In the given figure, find a + b.
OR
In figure, find the value of x.
Ans. Since AD is a straight line in the given figure, we obtain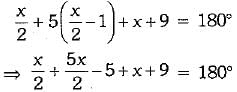
⇒ 4x + 4 = 180°
⇒ 4x = 176°
⇒ x = 44°
Now, a + b = 180° - (x + 9)°= 180° - (44 + 9)°
= 180° - 53° = 127°
OR
∵ EBF is a straight line
∴ (x + 3)°+ (x + 20)°+ (x + 7)° = 180°
⇒ x + 3° + x + 20° + x + 7°= 180°
⇒ 3x + 30° = 180°
⇒ 3x = 150°
⇒ x = 1500/3 = 500
Q.30. Express y in terms of x for the equation 4x + 7 y = 14. Check which of the points (0, 2), (7/2, 0) and (2, 1) lie on graph of this equation.
Ans. We have, 4x + 7 y = 14
⇒ 7 y = 14 - 4x
⇒ 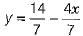 [dividing both sides by 7]
[dividing both sides by 7]
⇒ 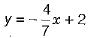
which s the required form.
Now, given points will lie on the graph of this equation, if they satisfy the given equation.
When x = 0, then y = -4/7 x 0 + 2 ⇒ y = 2, which is true.
So, (0, 2) lie on the line 4x + 7y = 14.
When x = 7/2, then y = 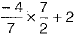
⇒ y = -2 + 2 = 0, which is true.
So, (7/2 ,0) will lie on the line 4x + 7y = 14.
Similarly, when x = 2, then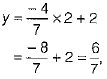
Which is not true.
So, the point (2, 1) will not lie on the line 4x +7y = 14.
Q.31. The hypotenuse of an isosceles right angled triangle has its ends at the points (1, 3) and (-4, 1). Find the equation of the legs (perpendicular sides) of the triangle.
OR
Find the equation of the ellipse whose centre is at the origin, foci are (1, 0) and (-1, 0) and eccentricity is 1/2.
Ans. Let ABC be the right isosceles triangle with hypotenuse AC such that the end points are A(1, 3) and C(- 4, 1), respectively.
Let m be the slope of a line making 45° angle with AC.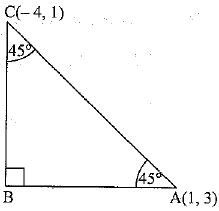
Slope of line AC = 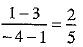
When 45° be the angle between AC and a line of slope m, then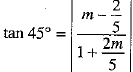
⇒ 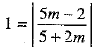
⇒ 5 + 2m = ±(5m - 2)
⇒ 5 + 2m = 5m - 2 or 5 + 2m = - (5m - 2)
⇒ 3m = 7 or 7m = - 3
⇒ m = 7/3 or m = - 3/7
Thus, the lines making 45° angle with AC having slope 7/3 or 3/7.
The possible equations of line AB are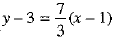 and
and 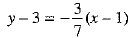
⇒ 3y - 9 = 7x - 7 and 7y - 21 = - 3x + 3
⇒ 7x - 3y + 2 = 0 and 3x + 7y - 24 = 0
The possible equations of line BC are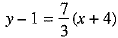 and
and 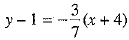
⇒ 3y - 3 = 7x + 28 and 7y - 7 = - 3x - 12
⇒ 7x - 3y + 31 = 0 and 3x + 7y + 5 = 0
Hence, the equations of the legs (perpendicular sides) are:
7x - 3y + 2 = 0 and 3x + 7y + 5 = 0
7x - 3y + 31 = 0 and 3x + 7y - 24 = 0
OR
Since the coordinates of the two foci S and S' be (1, 0) and (-1, 0), respectively.
∴ 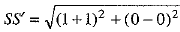
⇒ SS' = 2 ...(1)
Let 2a and 2b be the lengths of the major and minor axes of the required ellipse and e the eccentricity, then
SS' = 2ae ...(2)
From (1) and (2), we have
2ae = 2
⇒ ae = 1
⇒ 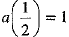
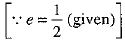
⇒ a = 2 ...(3)
Let P(x, y) be any point on the ellipse, then
SP + S'P = 2 a [By definition]
⇒ SP +S'P = 4 [using (3)]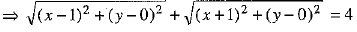
⇒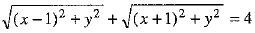
⇒ 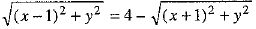
⇒ 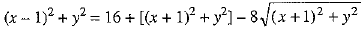 [Squaring both sides]
[Squaring both sides]
⇒ 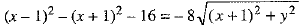
⇒ 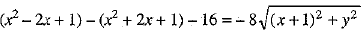
⇒ 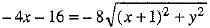
⇒ 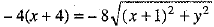
⇒ 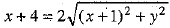 [Dividing both sides by - 4]
[Dividing both sides by - 4]
⇒ (x + 4)2 = 4[(x + 1)2 + y2]
⇒ x2 + 8x + 16= 4(x2 + 2x + 1) + 4y2
⇒ x2 + 8x + 16 = 4x2 + 8x + 4 + 4y2
⇒ (4x2 - x2) + 4y2 + (4 - 16) = 0
⇒ 3x2 + 4y2 - 12 = 0
⇒ 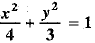
This is the required equation of the ellipse.
Q.32. In the given figure, AB and CD are two chords of a circle with centre O at a distance of 6 cm and 8 cm from O. If the radius of the circle is 10 cm, find the length of chords.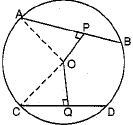
OR
In figure, ABCD is a cyclic quadrilateral; O is the centre of the circle. If ∠BOD = 160°, find the measure of ∠BPD.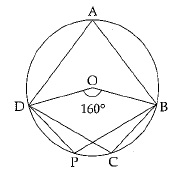
Ans. 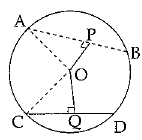
Join OA and OC.
Since, perpendicular from centre bisects the chord,
∴ 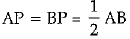
and 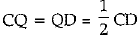
In ΔOAP, By Pythagoras theorem,
AP2 = OA2 - OP2
= 102 - 62 = 64
∴ AP = 8 cm or, AB = 16 cm
In ΔOQC,
CQ2 = OC2 - OQ2
= 102 - 82= 36
or, CQ = 6 cm, CD = 12 cm.
OR
Consider the arc BCD of the circle. The arc makes angle ∠BOD = 160° at the centre of the circle and ∠BAD at a point A on the circumference.
[From the same base the angle subtended at any point on the circumference of circle is half of that of the angle at centre.]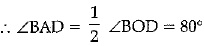
Now, ABPD is a cyclic quadrilateral
⇒ ∠BAD + ∠BPD = 180°
⇒ 80° + ∠BPD = 180°
⇒ ∠BPD = 100°
⇒ ∠BCD = 100°
[Angles in the same segment are equal]
Q.33. The parking charges of a car on domestic airport for first two hours is INR 100 and INR 50 for subsequent hours. Write down an equation and draw the graph of this data. Read the charges from the graph:
(i) for 3 hours (ii) for 4 hours.
Ans. Let total parking time be x hours and total charges be INR y.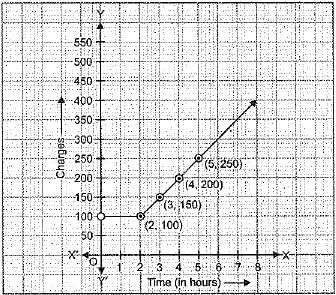
Since charges for first two hours is INR 100 and INR 50 for subsequent hours.
∴ We obtain the following linear equation
y = 100 + 50 (x - 2)
⇒ y = 50x ...(i)
Table of solutions is: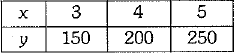
Plot these points (3, 150), (4, 200), (5, 250) on a graph paper and join them to get the required linear equation.
Clearly, from the graph
Charges for 3 hours is INR 150 and
Charges for 4 hours is INR 200.
Q.34. Express the following in a rational denominator.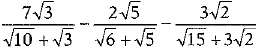
Ans. 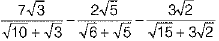
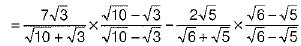
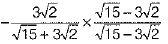 [by rationalisation]
[by rationalisation]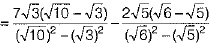
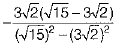
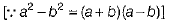
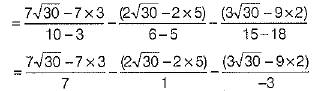
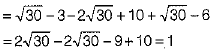
SECTION - D
Question numbers 35 to 40 carry 4 marks each.
Q.35. In a survey of 100 persons it was found that 28 read magazine A, 30 read magazine B, 42 read magazine C, 8 read magazines A and B, 10 read magazines A and C, 5 read magazines B and C and 3 read all the three magazines. Find how many read none of the three magazines and also find how many read magazine C only?
Ans. a, denote the number of persons who read only magazine A
g, denote the number of persons who read only magazine B
and f, denote the number of persons who read only magazine C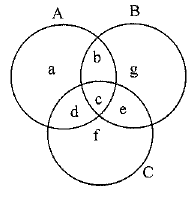
From the Venn-diagram, we have
n(A) = a + b + c + d
n(B) = b + c + g + e
n(C) = c + d + e + f
n(A ∩ B) = b + c
n(A ∩ C) = c + d
n(B ∩ C) = c + e
and n(A ∩ B ∩ C) = c
It is given that:
n(A ∩ B ∩ C) = 3 ⇒ c = 3
n(A ∩ B) = 8 ⇒ b + c = 8
⇒ b = 8 - 3 = 5
n(A ∩ C) = 10 ⇒ c + d = 10
⇒ d = 10 - 3 = 7
n(B ∩ C) = 5 ⇒ c + e = 5
⇒ e = 5 - 3 = 2
n(C) = 42
⇒ c + d + e + f = 42
⇒ 3 + 7 + 2 + f = 42
⇒ f = 42 - 3 - 7 - 2 = 30
n(B) = 30
⇒ b + g + c + e = 30
⇒ 5 + g + 3 + 2 = 30
⇒ g + 10 = 30
⇒ g = 30 - 10 = 20
n(A) = 28
⇒ a + b + c + d = 28
⇒ a + 5 + 3 + 7 =28
⇒ a + 15 = 28
⇒ a = 28 - 15 = 13
Number of persons who read none of the magazines
= n(A' ∩ B' ∩ C')
= n[(A ∪ B ∪ C)']
= n(U) - n(A ∪ B ∪ C)
= 100 - [a + b + c + d + e + f + g].
= 100 - [13 + 5 + 3 + 7 + 2 + 30 + 20]
=100 - 80
= 20
Number of persons who read magazine C only = f = 30.
Q.36. Verify if -2 and 3 are zeroes of the polynomial 2x3 - 3x2 - 11x + 6. Hence factorise the polynomial.
OR
The polynomials ax3 - 3x2 + 4 and 2x3 - 5x + a when divided by x - 2, leave the remainders p and q respectively. If p - 2q = 4, Find the value of a.
Ans. Let p(x) = 2x3 - 3x2 - 11x + 6
for x = -2
p(-2) = 2(-2)3 -3 (-2)2 - 11(-2) + 6
= -16 - 12 + 22 + 6
= - 28 + 28 = 0
for x = 3
p(3) = 2(3)3 - 3(3)2 - 11(3) + 6
= 54 - 27 - 33 + 6
= 60 - 60 = 0
So, -2 and 3 are zeros of the given polynomial.
Now (x + 2) (x - 3) = x2 - x - 6
Now we divide, p(x) = 2x3 - 3x2 - 11x + 6 by x2 - x - 6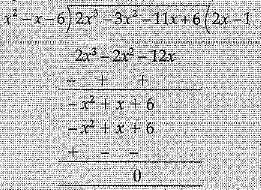
Hence p(x) = (x + 2) (x - 3) (2x - 1)
OR
Let f(x) =4 - 3x2 + ax3 and
g(x) = 2x3 - 5x + a
When f(x) is divided by (x - 2), then by Remainder Theorem
Remainder = f(2)
⇒ a(2)3 - 3(2)2 + 4 = p
⇒ 8a - 12 + 4 = p
⇒ 8a - 8 = p ...(1)
When g(x) is divided by (x -2), then by Remainder Theorem
Remainder = g(2)
⇒ 2(2)3 - 5(2) + a = q
⇒ 16 - 10 + a = q
⇒ 6 + a - q ...(2)
According to the question
p - 2q = 4
⇒ 8a - 8 - 2 (6+a) = 4 [By using (1) and (2)]
⇒ 8a - 2a = 4 + 8 + 12
⇒ 6a = 24
⇒ a = 4
Q.37. 4 years before, age of a mother was 3 times the age of her daughter. Write a linear equation to represent this situation and draw its graph.
Ans. Let the present age of mother be x years and that of her daughter be y years.
4 years before, the age of mother was (x - 4) years and the age of daughter was (y - 4) years.
∴ We have the following linear equation: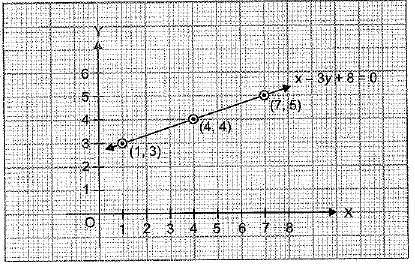
x - 4 = 3(y - 4)
⇒ x - 4 = 3y - 12
⇒ x - 4 - 3y + 12 = 0
⇒ x - 3y + 8 = 0 ...(i)
Put x = 1, in eq. (i)
⇒ 1 - 3y + 8 = 0
⇒ 3y = 9 ⇒ y = 3
Put x = 4, in eq. (i)
⇒ 4 - 3y + 8 = 0
⇒ 3y = 12 ⇒ y = 4
Put x = 7, in eq. (i)
⇒ 7 - 3y + 8 = 0
⇒ 3y = 15 ⇒ y = 5
To draw the graph, we use the following table: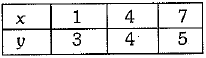
Q.38. If 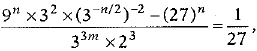 prove that m - n = 1
prove that m - n = 1
OR
Simplify 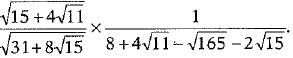
Ans. We have,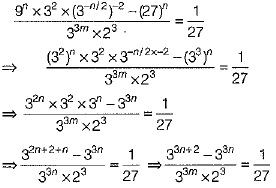
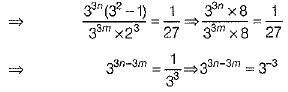 [on equating the exponent]
[on equating the exponent]
⇒ 3n - 3m = -3
⇒ n - m = -1 ⇒ m - n = 1
OR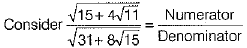
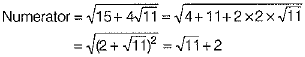
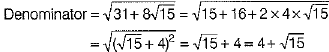

On rationalising, we get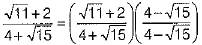
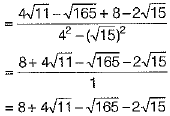
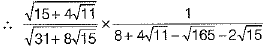
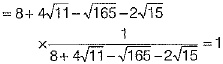
Q.39. Show that the middle term in the expansion of 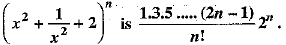
OR
Find n, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of 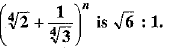
Ans. Given expression, 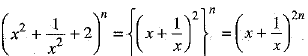
Here, index = 2n; so, total number of terms in the expansion = 2n + 1. which is odd.
Therefore there is only one mid-term, which is (n +1) the term.
In the expansion of 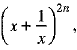 we have
we have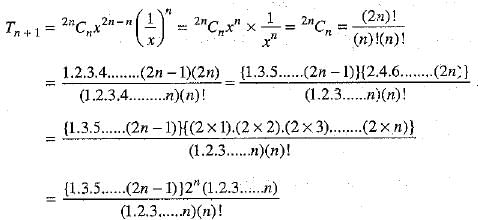
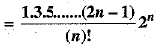
OR
Let Tr be the rth term from the beginning in the expansion of 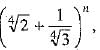 then
then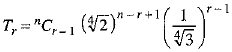
⇒ 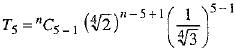
⇒ 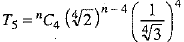 ...(1)
...(1)
Let T'r be the rth term from the end in the expansion of 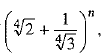 then,
then,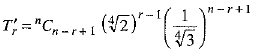
⇒ 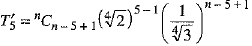
⇒ 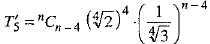 ...(2)
...(2)
It is given that the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of 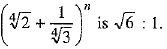
⇒ 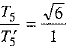
⇒ 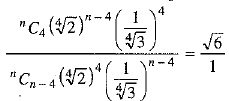 [using (1) and (2)]
[using (1) and (2)]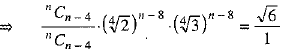
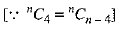
⇒ 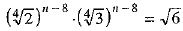
⇒ 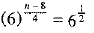
⇒ 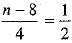
⇒ n - 8 = 2
⇒ n = 8 + 2
⇒ n = 10.
Q.40. Consider the marks out of 100, obtained by 50 students of a class in a test, given as below.
Draw a frequency polygon representing the data.
Ans.
| Marks | Number of Students |
| 0 - 20 | 15 |
| 20 - 40 | 10 |
| 40 - 60 | 10 |
| 60 - 80 | 11 |
| 80 - 100 | 4 |
Frequency polygon graph is ARCDEFG, is shown below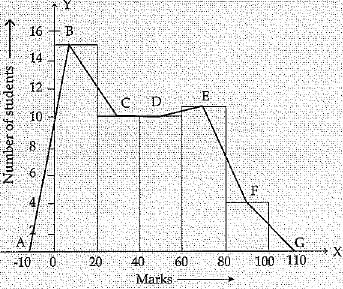
FAQs on Class 9 Math: Sample Question Paper- 11 (With Solutions)
| 1. What is the format of the Class 9 Math Sample Question Paper- 11? |  |
| 2. How many questions are included in the Class 9 Math Sample Question Paper- 11? |  |
| 3. Are the solutions provided for the Class 9 Math Sample Question Paper- 11? |  |
| 4. Can the Class 9 Math Sample Question Paper- 11 help in exam preparation? |  |
| 5. How can I access the Class 9 Math Sample Question Paper- 11? |  |














