Traditional Data Interpretation & Mathematical Constructs | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
| Table of contents |

|
| Introduction |

|
| What Is Traditional Data Interpretation? |

|
| Key Concepts in Data Interpretation |

|
| Handling the Ratio Comparison Situation: |

|
Introduction
As outlined in the preface, this book is structured into two sections: Traditional Data Interpretation (D1) and Logical DI. While this categorization has not been formally stipulated by any exam conducting body, it becomes apparent when analyzing questions from recent CAT and XAT papers. The distinction is evident as the skills essential for mastering each type of question are markedly different, akin to studying two distinct subjects. Therefore, to excel in aptitude exams like the CAT and the XAT, proficiency in both Traditional and Logical DI is imperative.
At present, our focus is directed towards Traditional DI.
What Is Traditional Data Interpretation?
- In the realm of Traditional Data Interpretation (DI), a typical question unfolds with data presented in the form of graphs, charts, or text, followed by questions that often necessitate extensive calculations. These questions typically revolve around key mathematical structures, and in the context of Traditional DI, it is essential to develop a grasp of important thought structures.
- A historical analysis of DI questions across various examinations reveals that these questions primarily fall into distinct quantitative divisions based on specific mathematical constructs:
- DI based on Averages and Alligations
- DI based on Percentages
- DI based on Ratio and Proportions
- DI based on Mixed concepts of the above
- DI based on Numerical Logic
- DI based on Set Theory
- DI sets based on miscellaneous concepts
- The ability to identify the underlying mathematical construct is pivotal during the initial reading of a DI set. This identification significantly influences the questioning possibilities that can arise from a given dataset, aiding in pre-assessing the difficulty level of the questions.
- Competence in recognizing the mathematical construct becomes crucial, as difficulty in handling a DI set typically stems from either an inability to understand the data set or a lack of proficiency in calculations. While solving this book, the focus is on developing strategies, processes, and techniques for accurate and swift calculations. Emphasizing the importance of familiarizing oneself with predictable calculation scenarios, the aim is to empower the student to face any calculation situation in exams like CAT, XAT, or other aptitude exams.
- By honing these skills, particularly in mastering calculation situations, students can build the confidence needed to navigate the DI section effectively. The belief that 'I can solve anything in DI' becomes attainable with controlled variables and a thorough preparation for known calculation scenarios.
- The subsequent discussion delves into various mathematical structures commonly used in Data Interpretation, using random questions from previous years' papers to illustrate problem-solving approaches.
Key Concepts in Data Interpretation
Averages
- The concept of average is fundamental in mathematics, representing one of the measures of central tendency alongside median and mode. Averages find extensive use in statistical analysis and comparisons across various scenarios, such as a cricket batsman's batting average, a bowler's bowling average, the average price of a commodity, or the average sales per territory for a product.
- Mathematically, the average of a group of numbers is calculated as the sum of the numbers divided by the count of numbers.
- In the context of Data Interpretation (DI), the Assumed Average Approach is a powerful method for estimating the average of a group of numbers. This approach involves assuming an average and then adjusting it based on deviations to arrive at the correct average. The versatility of this method is highlighted by the fact that the correct average is obtained regardless of the value chosen for the assumed average.
- To illustrate this approach, let's consider a set of 6 numbers: 12, 17, 8, 22, 15, and 34. Assuming an average of 22, the correct average is calculated as 18. This process is applicable irrespective of the assumed average value.
- The Assumed Average Approach proves invaluable in scenarios where the average or total of a set of numbers needs calculation. For example, it can be used to find a missing number in a series or determine the average of large numbers efficiently.
- In practice, this approach is particularly useful for situations where large numbers need to be averaged. For instance, given five five-digit numbers—37484, 52776, 81447, 93829, and 78561—the Assumed Average Approach helps break down the calculation into manageable steps. By first calculating the average of the leftmost two digits and then incorporating the average of the last three digits, a close approximation of the overall average is achieved. This method proves effective in scenarios where precision is needed, and the range derived from the minimum and maximum values is usually sufficient for answering questions.
- In summary, mastering the Assumed Average Approach equips students with a powerful tool for handling various DI situations, enabling them to efficiently calculate averages and totals in a range of scenarios encountered in exams like CAT.
Alligations
The concept of alligation frequently arises in quantitative scenarios involving weighted averages. Weighted average occurs when multiple groups with their respective averages are combined to form a composite group with a single average. The formula for weighted average considers the number of units in each group as the weightage, influencing the overall average of the composite group.
In a weighted average situation, the formula for the weighted average (Aw) is given by:
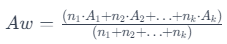
The actual values of the populations do not affect the weighted average; rather, it depends on the ratio of the populations. Therefore, changing the population values while maintaining the ratio does not alter the weighted average.
The alligation situation is a visual representation on the number line, encapsulating the structure of thinking for two-group weighted averages. It is particularly useful for solving problems where the ratio of mixing (n1:n2) is known, and the objective is to find the weighted average (Aw) or the individual averages (A1,A2).
Cases in Alligation:
- Case 1: When A1,A2, and Aw are known, and the ratio n1:n2 is sought.
- Case 2: When A1,A2, and the ratio n1:n2 are known, and Aw is sought.
- Case 3: When the ratio n1:n2 is known, and eitherA1 or A2 is known, and the other average is sought.
The three cases are visualized on the number line, representing the averages A1,Aw,A2 in that order. The distances between these points on the number line correspond to the ratios n1, n2, and n1+n2, respectively.
Understanding and applying the alligation method proves beneficial in solving problems related to two-group weighted averages efficiently.
The processes for the 3 cases illustrated above can then be illustrated below:
Illustration 1: On mixing two classes of students having average marks 25 and 40 respectively, the overall average obtained is 30 marks. Find
(a) the ratio in which the classes were mixed.
(b) the number of students in the first class if the second class had 30 students.
Solution: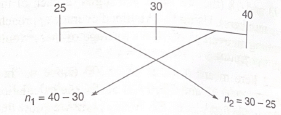
Hence, ratio is 2: 1, and the first class has 60 students.
Case 2 A1, A2, n1, and n2, are known; Aw is unknown.
3. Percentages
A. Percentage Calculations:
In percentage calculations, there are two basic structures frequently used in Data Interpretation:
Percentage Rule for Calculating Percentage Values through Additions:
This method, previously discussed in the book's earlier section on Divisions, Percentages, and Ratio Comparisons, involves calculating percentage values through additions. Continued practice with this method is recommended.
B. Percentage Change in a Product:
When dealing with the percentage change in a product, a specific formula is applied to assess the change in a product resulting from changes in its components.
For instance, consider a product of two variables, 10 × 10. If the first variable changes to 11 with a 10% increase and the second variable changes to 12 with a 20% increase, the percentage change in the product can be calculated using the formula: 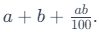
Hence, the required percentage change would be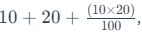 where 10 and 20 are the respective percentage changes in the two parts of the product.
where 10 and 20 are the respective percentage changes in the two parts of the product.
While this formula is commonly taught as a shortcut, a more intuitive and easier solution involves visualizing the changes step by step:
Hence, the final product shows a 32% increase.
Similarly, for a product initially at 10×10×10 that becomes 11×12×13, the following Percentage Change in a Product (PCG) approach is used:
The final product sees a 71.6% increase. Importantly, the order in which the respective percentage changes are applied does not affect the result. This process is reminiscent of calculating successive percentage changes.
It's noteworthy that this approach simplifies complex percentage change calculations in product scenarios.
Application for DI:
Percentage Change in Sales Revenue of Scooters:
Suppose you have two pie charts representing the sales revenue of scooters for a company in two different years. To calculate the percentage change in sales revenue from year one to year two, the formula for percentage change is applied:
This calculation, however, can be complex. Alternatively, the Product Change application of Percentage Change in a Product (PCG) simplifies this process. The solution involves assessing the product for each year:
Product for Year One: 0.2347×17342.34
Product for Year Two: 0.2655×19443.56
Approximating these values, we get 234 × 173 and 265 × 194, respectively. The overall percentage change relies on two individual percentage changes:
234234 increases to 265: A percentage change of 31/234≈13.2% (calculated using the percentage rule for calculating the percentage value of the ratio).
173173 increases to 194: A percentage change of approximately 12%.
Using PCG, the overall percentage change is calculated as follows:
Hence, there is a 26.76% increase in the product's value. This method provides an accurate and efficient solution to the question. Note that although the value on the calculator for the full calculation without approximations is 26.82%, the method's accuracy is deemed satisfactory.
4. Ratios
Handling Large Ratios in Data Interpretation:
In data interpretation, you often encounter scenarios involving large ratios, such as  To handle such cases efficiently, consider simplifying the calculation by focusing on smaller ratios. For instance, if the decimal value of an 8-digit divided by an 8-digit number is 0.abcdefgh, you can transform the problem into a 3-digit divided by 3-digit calculation while maintaining adequate accuracy.
To handle such cases efficiently, consider simplifying the calculation by focusing on smaller ratios. For instance, if the decimal value of an 8-digit divided by an 8-digit number is 0.abcdefgh, you can transform the problem into a 3-digit divided by 3-digit calculation while maintaining adequate accuracy.
Let's demonstrate this concept with the ratio Instead of performing the calculation for the entire ratio, calculate
Instead of performing the calculation for the entire ratio, calculate or, in more challenging cases,
or, in more challenging cases,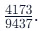 Begin by finding the percentage value of
Begin by finding the percentage value of 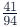 using the previously explained percentage rule.
using the previously explained percentage rule.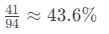
Therefore, the decimal value of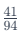 is 0.436 In cases where you need to calculate
is 0.436 In cases where you need to calculate 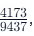 consider adjusting the value based on the last two digits:
consider adjusting the value based on the last two digits: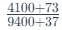
If the addition ratio were equal to the original ratio, the answer would remain 0.436. However, since the addition ratio usually differs, adjustments are necessary.
Determine the numerator addition (x) required to avoid changing the ratio with a fixed denominator addition of 37: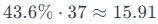
So, if the numerator addition were 16, the ratio would remain unchanged: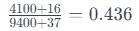
Now, calculate the original ratio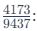

Approximately, 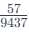 9.4 added six times gets close to 57). Thus, the correct answer is:
9.4 added six times gets close to 57). Thus, the correct answer is: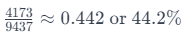
This method simplifies complex calculations by breaking them down into two-digit ratio calculations, providing an efficient approach for data interpretation. Extensive practice is recommended to master this technique for handling various scenarios in examinations.
Handling the Ratio Comparison Situation:
Effective Ratio Comparison:
In the preceding section of this book, various methods for ratio comparison were discussed. Now, let's delve into another powerful method, potentially the most potent one for comparing ratios.
Ratio comparisons typically involve four fundamental scenarios:
- Numerator increases, denominator decreases - The ratio rises, requiring no specific calculations.
- Numerator decreases, denominator increases - The ratio declines, necessitating no complex computations.
- Numerator increases, denominator increases.
- Numerator decreases, denominator decreases.
It's essential to note that situations 3 and 4 are opposite to each other. Understanding how to handle the case of the numerator increasing and denominator increasing allows you to tackle the case of the numerator decreasing and denominator decreasing by merely reversing the ratios. For instance, comparing 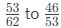 (both numerator and denominator decreasing) is analogous to comparing
(both numerator and denominator decreasing) is analogous to comparing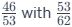 (both numerator and denominator increasing).
(both numerator and denominator increasing).
In this scenario, the change in the ratio depends on the relative impact of the numerator's and denominator's alterations. Employing the logic of the ratio of additions streamlines the comparison process. With some practice, even in closely contested situations, discerning which ratio is larger becomes second nature.
Consider comparing While calculators may yield values like 0.8679 and 0.8548, respectively, the ratio of additions logic interprets this as:
While calculators may yield values like 0.8679 and 0.8548, respectively, the ratio of additions logic interprets this as: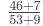
Upon evaluating, it's evident that 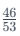 is above 80%, while
is above 80%, while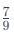 is 77.77%, below 80%. Since the ratio of additions is smaller than the original ratio, the new ratio is smaller.
is 77.77%, below 80%. Since the ratio of additions is smaller than the original ratio, the new ratio is smaller.
Mastering this ratio comparison process is highly beneficial, given its repetitive nature in data interpretation. Regular practice will solidify this method as your default approach, significantly enhancing your proficiency in solving data interpretation problems.
Now, let's transition to addressing specific traditional DI questions, experiencing the scenarios DI presents, and understanding effective problem-solving strategies.
|
100 videos|180 docs|99 tests
|
FAQs on Traditional Data Interpretation & Mathematical Constructs - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What is traditional data interpretation? |  |
| 2. What are the key concepts in data interpretation? |  |
| 3. How to handle the ratio comparison situation in traditional data interpretation? |  |
| 4. What are some frequently asked questions (FAQs) about traditional data interpretation? |  |
| 5. What mathematical constructs does traditional data interpretation use? |  |















