Class 9 Math: Sample Question Paper- 4 (With Solutions) PDF Download
SECTION - A
Questions 1 to 20 carry 1 mark each.
Q.1. The value of 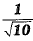 when
when 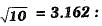
(a) 0.3162
(b) 31.62
(c) 0.0316
(d) 316.2
Ans: (a) 0.316 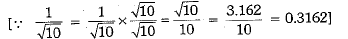
Q.2. The value of tan 1° tan 2° tan 3° ............. tan 89° is equal to
(a) 0
(b) 1
(c) 2
(d) √2
Ans: Choice (b) is correct.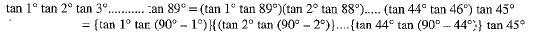
Q.3. Points (-4,0) and (7,0) are
(a) lies on Y-axis
(b) lies on X-axis
(c) in first quadrart
(d) in second quadrant
Ans: (b) Point (-4, 0)and (7, 0) lie on X-axis.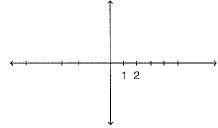
Q.4. If the graph of equation 2x + ky - 10k, intersect x-axis at point (5, 0), then k is :
(a) 0
(b) - 1
(c) 2
(d) 1
Ans: Correct option: (d)
(5,0) is a point on lies 2x + ky - 10k
∴ 10 = 10k ⇒ k = 1
Q.5. In the given figure, if l || m and ∠p:∠q = 4:5, then ∠r is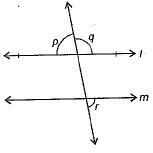
(a) 60°
(b) 80°
(c) 90°
(d) 100°
Ans: (b) 80°
[∵ Let ∠p = 4x and ∠q - 5x
Now, ∠p + ∠q = 180° [linear, pair axiom]
⇒ 4x + 5x = 180o
⇒ 9x = 180o
x = 20o
∴ ∠r = ∠p = 4x = 4 x 20o = 80o]
Q.6. Two finite sets have m and n elements. The total number of subsets of first set is 56 more than total number of subsets of second set, then the values of m and n are :
(a) 6 and 3
(b) 3 and 6
(c) 3 and 9
(d) 6 and 9
Ans: Choice (a) is correct.
Suppose A and B has m and n elements respectively.
∴ Number of subsets of set A = 2m
and number of subsets of set B = 2n
According to given condition, we have
2m - 2n = 56
⇒ 2n(2m-n - 1 ) = 8 x 7
⇒ 2n(2m-n - 1 ) = 23 x (8 - 1)
⇒ 2n(2m-n - 1 ) = 23 x (23 - 1)
∴ n= 3 and m - n= 3
⇒ n = 3 and m = 3 + 3 = 6
Q.7. The graph of the equation x = a is a straight line parallel to
(a) X-axis
(b) Y-axis
(c) Both of them
(d) None of these
Ans: (b) The graph of the equation x = a is a straight line parallel to Y-axis.
Q.8. In a sample study of 642 people, it was found that 514 people have a high school certificate. If a person is selected at random, the probability that the person has a high school certificate is
(a) 0.5
(b) 0.6
(c) 0.7
(d) 0.8
Ans: Correct option: (d)
Explanation: Total no. of people = 642
No. of people with high school certificate = 514
P (person with high school certificate) =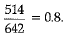
Q.9. In a cylinder, radius is doubled and height is halved, curved surface area will be
(a) halved
(b) doubled
(c) same
(d) four times
Ans: (c) same
[∴ Let r and h be radius and height of the cylinder, then C.S.A. = 2πrh Now, radius is doubled and height is halved
∴ New radius = 2r and new height =h/2
New C.S.A. - 2π x 2r x h/2 = 2πrh]
Q.10. The coefficients of variation for batsmen A and B are 3.07% and 3.04% respectively, then batsman B is more consistent because :
(a) The batsman B is more consistent as co-efficient of variation for batsman B > coefficient of variation for batsman A.
(b) The batsman B is more consistent as shows more variability.
(c) The batsman B is more consistent because of the coefficient of variation for batsman B < the coefficient of variation for batsman A:
(d) None of the above is correct.
Ans: Choice (c) is correct.
Questions 11 to 15 carry one mark each.
Q.11. Degree of the zero polynomial is .........
Ans: The degree of zero polynomial is not defined.
Q.12. ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24 cm2, then ar (ABC) = 24 cm2
Ans: False.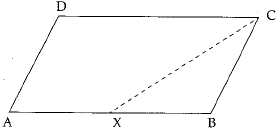
Explanation: We have given that AB CD is a parallelogram and X is the midpoint of AB.
Now, ar (ABCD) = ar (AXCD) + ar (XBC) ...(1)
Diagonal AC of a parallelogram divides it into two triangles of equal area.
ar (ABCD) = 2ar (ABC) ...(2)
Again, X is the mid-point of AB, So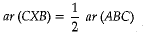 ...(3)
...(3)
[Median divides the triangle in two triangles of equal area]
From Eq (1)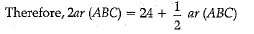 [Using (1), (2) and (3)]
[Using (1), (2) and (3)]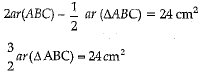
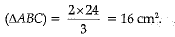
Q.13. The diagonals of a square are ................and .................each other at ..................
Ans: equal, bisect, right angle
Q.14. Equation of a straight line through (2,3) and making an angle of 60° with the positive direction of x-axis is ___________.
Ans: 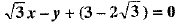
Required line is y - 3 = tan 60°(x - 2)
⇒ 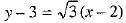
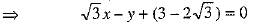
Q.15. Facts or figure, collected with a definite purpose are called...
Ans: Facts or figure, collected with a definite purpose are called data.
Questions 16 to 20 carry one mark each
Q.16. Find the value of x from the adjacent figure.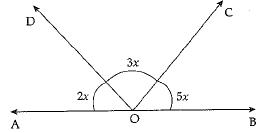
Ans: 2x + 3x + 5x = 180°
10x = 180°
x = 18°
Q.17. Find the percentage increase in the area of a triangle if its every side is doubled.
Ans. Let a, b and c be the sides of a triangle. Let s be the semi-perimeter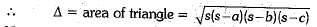
Now, each side of the triangle is doubled.
∴ New dimensions of the triangle are 2a, 2b, 2c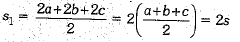
∴ Δ1 = area of new triangle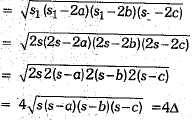

Hence, the percentage increase in area of a triangle if its every side is doubled, is 300%
Q.18. Find the slope of a line which passes through the origin, and the mid-point of the line segment joining the points (0,-4) and (8, 0).
Ans: The equation of a line passing through the origin and having a slope m is y = mx...(1)
If the line (1) passes through the mid-point of the line joining the points (0,-4) and (8,0), i.e., through the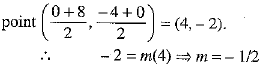
Hence, the slope of a line passes through the origin is -1/2.
Q.19. In the given figure, ∠1 = 60° and ∠6 = 120°.
Show that the lines m and n are parallel.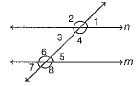
Ans: Here, ∠1 + ∠2 = 180° [linear pair axiom]
60° + ∠2 = 180°
⇒ ∠2 = 120°
We have, ∠6 = 120° ⇒ ∠2 = ∠6 = 120°
which are corresponding angles.
Hence, m || n
Q.20. Factorise : y2 - 8y + 16.
OR
Evaluate : 2492 - 2482
Ans: y2 - 8y +16 = y2 - 2 x 4y + 42 = (y - 4)2
OR
2492 - 2482
= (249 +248) (249 - 248)
= 497 x 1
= 497
SECTION - B
Questions 21 to 26 carry two marks each
Q.21. Simplify 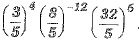
Or
Simplify 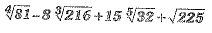
Ans: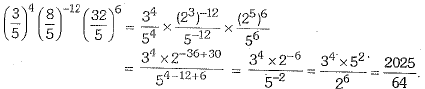
Or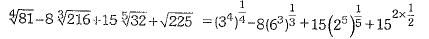
= 3-8 x 6 + 15 x 2 + 15
= 3-48+30+15 = 48-48 =0
Q.22. A and B are mutually exclusive events of an experiment. If P(A) = 0.4 and P(B) = 0.5, find 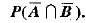
Ans: We have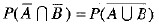
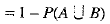
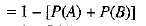 [ ∴ A and B are mutually exclusive]
[ ∴ A and B are mutually exclusive]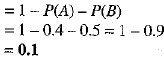
Q.23. Construct an equilateral triangle, given its side AB =6 cm.
Ans: Given, length of equilateral side = 6 cm
Steps of construction
(i) First, draw a line segment SC = 6 cm.
(ii) Taking S and C as centre and radius 6 cm, draw two arcs.
(iii) The arc of step (ii) cut any point A join the lines. AB and AC.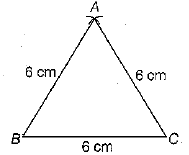
Thus, ΔABC is an equilateral triangle.
Q.24. An isosceles right triangle has area 200 cm2. Find the length of its hypotenuse.
Ans: Given: ABC is an isosceles right triangle.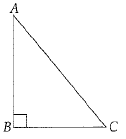
∴ Hypotenuse (AC) is the longest side of ΔABC.
∴ ∠B = 90° and AB = BC
or (Δ ABC) = 200 cm2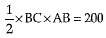
BC2 = 400 [∴AB = BC]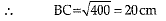
By using Pythagoras theorem
AC2 = AB2 + BC2
=BC2+ BC2 (∴ AB = BC)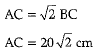
AC=20 x 1.414= 28.280 cm
AC = 28.28 cm
Q.25. If the mean of the following data is 20.2, find the value of p.
Ans. 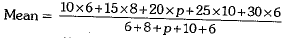
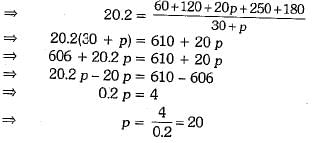
Q.26. Determine the values of a and b so that the points (a,b,3), (2,0,-1) and (1,-1,-3) are collinear.
Ans: The given points are P(a, b, 3), Q(2,0,-1) and R(1,-1,-3).
Let the point P divide the line joining Q and R in the ratio k:1.
The coordinates of the point P are 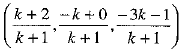
But the coordinates of P are given to be (a, b, 3).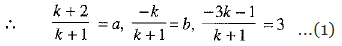
From last equation of (1), we have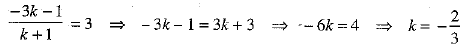
Putting value of k in (1), we have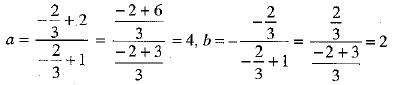
⇒ a = 4 and b = 2
Or
Determine the point in yz-plane which is equidistant from three points A(1,-1,0), B(2,1, 2) and C( 3, 2, - 1).
Ans: We know that x-coordinate of every point on yz-plane is zero. Let P(0, y, z) be any point in yz-plane such that
PA = PB = PC.
Since, PA = PB
⇒ PA2 = PB2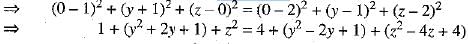
⇒ 4y + 4z = 7
⇒ 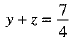 ...(1)
...(1)
Now,
PB - PC
PB2 = PC2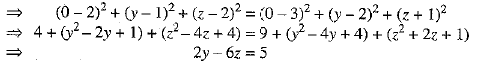
⇒ 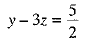 ...(2)
...(2)
Subtracting (2) from (1), we get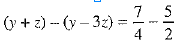
⇒ 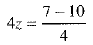
⇒ 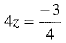
⇒ 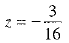
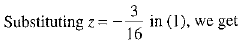
⇒ 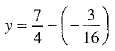
⇒ 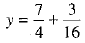
⇒ 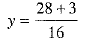
⇒ 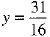
Hence, the required point in yz-plane is 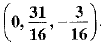
SECTION - C
Questions 27 to 34 carry 3 marks each
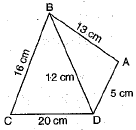
Q.27. The sides of a quadrilateral ABCD are AB = 13 cm , BC = 16 cm, CD = 20 cm and DA = 5 cm. If BD = 12 cm, find the area of the quadrilateral using Heron’s formula.
Ans: Here, given quadrilateral ABCD is divided into two triangles, ΔABD and ΔBCD.
For ΔABD,
Let a = 13 cm, b = 12 cm and c = 5 cm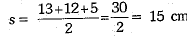
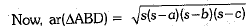
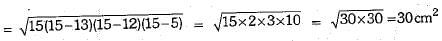
For ΔBCD,
Let a = 16 cm, b = 20 cm, c = 12 cm
∴ 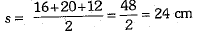
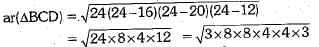
= 8 x 4 x 3 = 96 cm2
Now, ar(quad. ABCD) = ar(ΔABD) + ar(ΔBCD)
= 30 +96 =126 cm2
Q.28. Find the equation of the circle which passes through the points (2, -2), (3,4) and has its centre on the line 2x + 2y = 7.
Ans: Let the required equation of the circle with centre (h, k) and radius r be
(x - h)2 + (y - k)2 = r2 ...(1)
Since the circle passes through (2, -2) and (3,4), we have
(2 - h)2 + (-2 - k)2 = r2 ...(2)
and (3 - h)2 + (4 - k)2 - r2 ...(3)
From (3) and (4), we have
(2 - h)2 + (-2 -k)2 = (3 - h)2 + (4 - k)2
⇒ (2 - h)2 - (3 - h)2 = (4 - k)2 - ( - 2 - k)2
⇒ (2 - h + 3 - h)(2 - h - 3 + h) ={4 - k + (- 2 - k)}{4 - k - (- 2 - k)}
⇒ (5 - 2h)(- 1) = (2 - 2k)(6)
⇒ -5 + 2h = 12 - 12k
⇒ 2h + 12k =17 ...(4)
Also, since the centre (h, k) lies on the line 2x + 2y = 7, we have
2h + 2k = 7 ...(5)
Subtracting (5) from (4), we get
10k = 10
⇒ k=1 ...(6)
Substituting k = 1 in (5), we get
2h +2 = 7
⇒ 2h = 5
⇒ h=5/2 ...(7)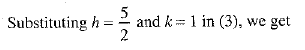
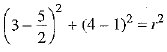
⇒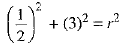
⇒ 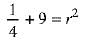
⇒ 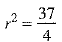 ...(8)
...(8)
From (1), (6), (7) and (8), we get the required equation of the circle as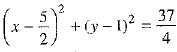
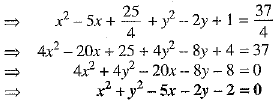
Or
Find the equation of the circle touching positive y-axis at a distance of 4 units from the origin and cutting intercepts of 6 units on positive x-axis.
Ans: As shown in the figure, let AB - 6 and OC - 4 as given in the question.
Let equation of the circle be
x2 + y2 + 2gx + 2fy + c = 0 ...(1)
At A or B,y = 0. Then
x2 + 2gx + c = 0
Let coordinates of A be (x1,0) and B be (x2,0).
Then x1 + x2 = - 2g and x1.x2 = c
Also AB - x2 - x1 = 6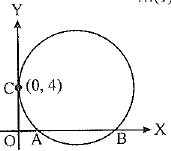
Now,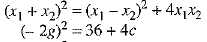
or 4g2 = 36 + 4c
or g2 = 9 + c ...(2)
Further, at C we have x = 0
Then from (1), y2 + 2fy + c = 0 ...(3)
Since equation (3) has real equal roots, we have
(2f)2-4(1)c = 0 [D = B2 - 4AC = 0]
or 4f2 - 4c = 0
or f2 = c ...(4)
At C,y = 4. From (3), we get
42 + 2f(4) + c = 0
or 16 + 8f+ c = 0
or c = - 16 - 8f ...(5)
From (4) and (5), we have
f2 = - 16 - 8f
or
f2 + 8f + 16 = 0
or (f + 4)2 = 0 ⇒ f = - 4 ⇒ c = 16 [From (4)]
Now from (2) g2 = 9 + 16 = 25 ⇒ g = ± 5
Putting values of g = ± 5, f = - 4 and c = 16 in (1), we get equations of circles as
x2 +y2 + 10x - 8y + 16 = 0
Q.29. Find three irrational numbers between 5/7 and 9/11.
Or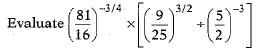
Ans: By Song divsion, we have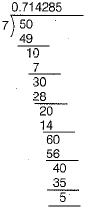
∴ 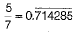
Also,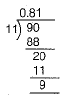
∴ 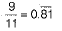
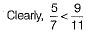
So, we can consider three irrational numbers between 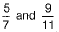 which are non-terminating non-repeating decimals as follows
which are non-terminating non-repeating decimals as follows
0.72072007200072...
0.73073007300073...
0.74074007400074...
or
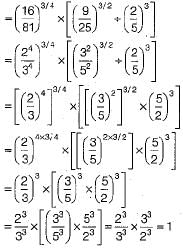
Q.30. ABCD is a parallelogram and line segments AX, CY bisect the angles A and C, respectively. Show that AX || CY.
Ans. Given : ABCD is a parallelogram. AX and CY bisect the angle A and C respectively.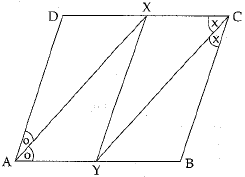
To Trove : AX || CY
Construction: Join XY
Proof: ABCD is a parallelogram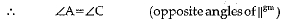
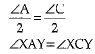
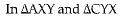

Q.31. From the given graph, answer the following
(i) Write the points whose abscissa is 0.
(ii) Write the points whose ordinate is o.
(iii) Write the points whose abscissa is -5.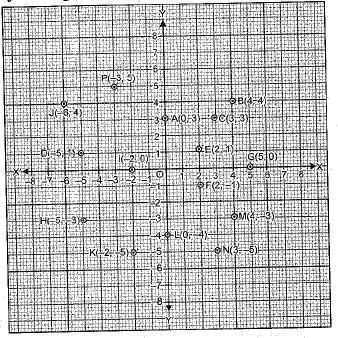
Ans: (i) A(0, 3), L(0, -4), O(0,0)
(ii) G(5, 0), l(-2, o), O(0, 0)
(iii) D(-5, 1) and H(-5, -3).
Q.32. Find the derivative of 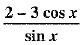 with respect to x.
with respect to x.
Ans: Here,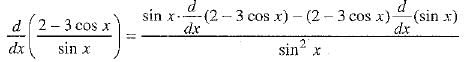
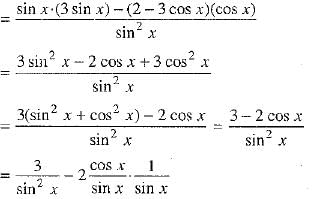
= 3 cosec2 x - 2 cosec x cot x
Q.33. AB and CD are respectively, the smallest and the longest sides of a quadrilateral ABCD. Show that ∠A > ∠C and ∠B > ∠D.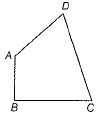
Ans: First, draw the diagonal AC.
In ΔABC, AB is the' shortest side.
[∵ angle opposite to the shortest sice is smaller]
In ΔACD, CD is the longest side.
[∴ angle opposite to the longest side is longer]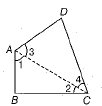
On adding Eqs. (i) and (ii), we get.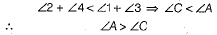
Now, draw the diagonal BD in ΔABD, AB is the shortest side.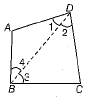
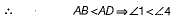 ...(iii)
...(iii)
[∵ angle opposite to the shortest side is smaller]
In A BCD, CD is the longest side.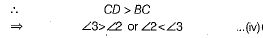
[angle opposite to the longest side is longer]
On adding Eqs. (iii) and (iv), we get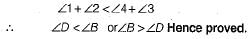
Q.34. Two dice are thrown simultaneously 500 times. Each time the sum of two numbers appearing on them is noted and recorded in the following table :
From the above data, what is the probability of getting a sum :
(i) More than 10.
(ii) Betweeen 8 and 12.
OR
Fifty seeds were selected at random from each 5 bags seeds and were kept under standardized conditions favourable to germination. After few days, the number of seeds which had germinated in each collection were counted and recorded as follows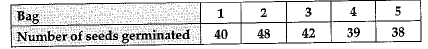
What is the probability of germination of
(i) More than 40 seeds in a bag
(ii) 49 seeds in a bag
(iii) More than 35 seeds in a bag
Ans: (i) Probability of getting a sum more than 10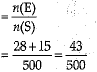
(ii) Favourable events n(E) = 8 < n(E)<12
n(E) = 53 + 46 + 28 = 127
Probability of getting a sum between 8 and 12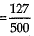
Or
Total number of bags = 5
(i) P(more than 40 seeds in a bag) = 2/5 = 0.4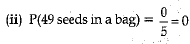

SECTION - D
Questions 35 to 40 carry 4 marks each
Q.35. Simplify: 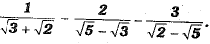
Or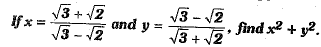
Ans: Here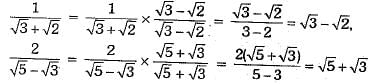
and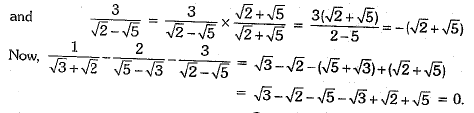
Or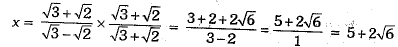
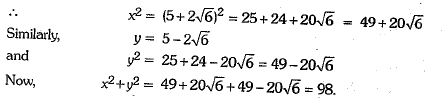
Q.36. If α and β are acute angles and cos 2α =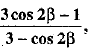 show that
show that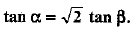
Ans. 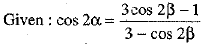
⇒ 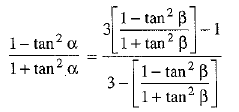
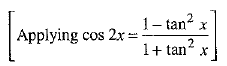
⇒ 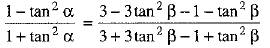
⇒ 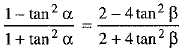
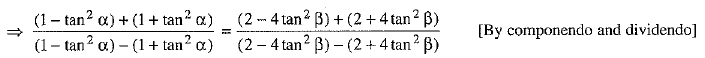
⇒ 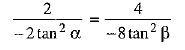
⇒ 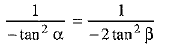
⇒ 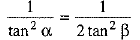
⇒ 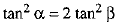
⇒ 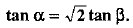
or
Prove that : cos2 x + cos2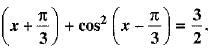
Ans: We have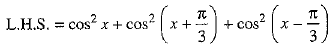
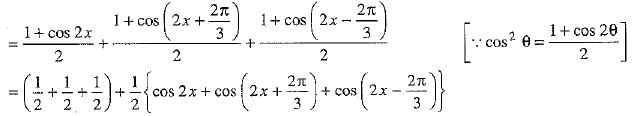
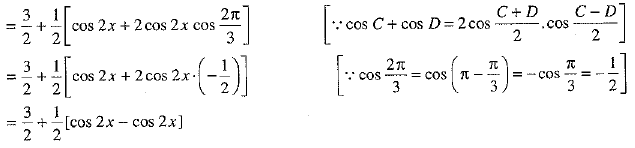
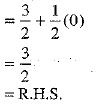
Q.37. A park in the shape of quadrilateral ABCD has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5m and AD = 8m. How much area does it occupy?
Or
A kite in the shape of a square with each diagonal 36 cm and having a tail in the shape of an isosceles triangle of base 10 cm and equal side 6 cm, is made of three different shades as shown in the adjoining figure. How much paper of each shade has been used in it? [Given, 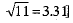
Ans. Given, a quadrilateral ABCD in which AB = 9 m, BC = 12 m, CD = 5m, AD = 8m and ∠C = 90°.
Join the diagonal BD.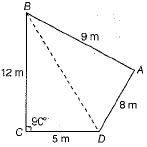
In ABCD, we have
(BD)2 = (BC)2 + (CD)2 [by Pythagoras theorem]
= (12)2 + (E)2 = 144+ 25 = 169
⇒ BD = 13m [taking positive square root]
∴ ΔBCD is a right angled triangle.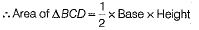
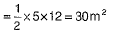
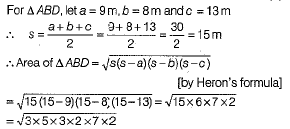
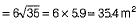
Now, area of quadrilateral ABCD
= Area of ΔBCD + Area of ΔABD
= 30+35.4=65.4 m2
Hence, the area of park is 655 m2
Or
One shaded portion is ΔABD.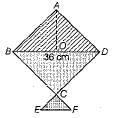
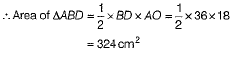
∵ Kite is the shape of square, so diagonals are equal and bisect each other
Second shaded portion is ΔBCD.
and area of ΔBCD = area of is ΔABD = 324 cm2
Third shaded portion is ΔCEF in which
CE = CF = 6 cm and EF = 10 cm.
Here, a = 6 cm, b = 6 cm and c = 10 cm
∴ 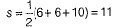
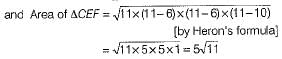
= 5x3.31 = 16.55 cm2
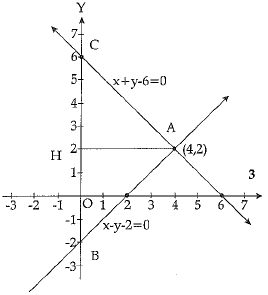
Q.38. Draw the graph of two lines whose equations are x+y - 6=0 and x-y - 2 = 0, on the same graph paper. Find the area of triangle formed by the two lines and y axis.
Ans: Given of lines are x + y - 6 = 0
and x - y - 2 = 0 Table for line x + y - 6 = 0 or y = 6 - x is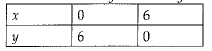
Table for line x-y-2 = 0 ox y = x-2 is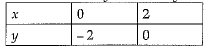
Q.39. Two hemispherical domes are to be painted as shown in the given figure. If the circum-ferences of the bases of the domes are 17.6 cm and 70.4 cm respectively, then find the cost of painting at the rate of Rs 10 per cm2.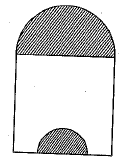
Ans: Let radii of the bases of two hemispherical domes be r and R.
∵ 2πr =17.6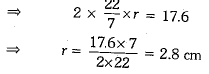
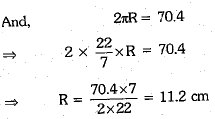
Now, areas of two hemispherical domes = 2πr2 + 2πR2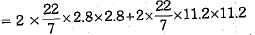
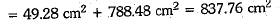
Cost of painting at the rate of Rs 10 per cm2
= Rs 10 x 837.76 = Rs 8377.60
Q.40. In how many of the distinct permutations of the letters in MISSISSIPPI do the four I's not come together ?
Ans: Total number of letters in MISSISSIPPI = 11
Out of these
I is repeated four times
S is repeated four times
P is repeated two times
and rest are different.
Thus, total number of distinct permutations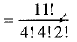
If four I’s always come together, then we have to arrange 7 (11 - 4) other letters + 1 group of four I’s (IIII) = 8 letters, that can be done in 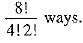
Hence, the total number of distinct permutations of the letters in MISSISSIPPI such that four I’s do not come together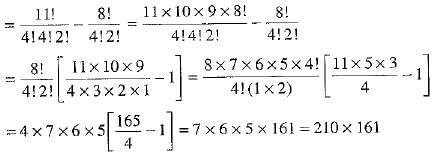
= 33810














