Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1. Define cumulative frequency distribution.
Solution 1: Cumulative frequency distribution:
A table which displays the manner in which cumulative frequencies are distributed over various classes is called a cumulative frequency distribution or cumulative frequency distribution table.
Q2. Explain the difference between a frequency distribution and a cumulative frequency distribution.
Solution 2:
Frequency table or frequency distribution is a method to represent raw data in the form from which one can easily understand the information contained in a raw data, where as a table which plays the manner in which cumulative frequencies are distributed over various classes is called a cumulative frequency distribution.
Q3. The marks scored by 55 students in a test are given below:
| Marks | 0 - 5 | 5 - 10 | 10 - 15 | 15 - 20 | 20 - 25 | 25 - 30 | 30 - 35 |
| No. of students | 2 | 6 | 13 | 17 | 11 | 4 | 2 |
Prepare a cumulative frequency table
Solution 3:
| Marks | No. of students | Marks | Cumulative Frequency |
| 0 - 5 | 2 | Less than 5 | 2 |
| 5 - 10 | 6 | Less than 10 | 8 |
| 10 - 15 | 13 | Less than 15 | 21 |
| 15 - 20 | 17 | Less than 20 | 38 |
| 20 - 25 | 11 | Less than 25 | 49 |
| 25 - 30 | 4 | Less than 30 | 53 |
| 30 - 35 | 2 | Less than 35 | 55 |
| N = 55 |
Q4. Following are the ages of 360 patients getting medical treatment in a hospital on a day.
| Age(in years) | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 |
| No of patients | 90 | 50 | 60 | 80 | 50 | 30 |
Construct a cumulative frequency table.
Solution 4:
| Age (in years) | No. of students | Marks | Cumulative Frequency |
| 10 - 20 | 90 | Less than 20 | 90 |
| 20 - 30 | 50 | Less than 30 | 140 |
| 30 - 40 | 60 | Less than 40 | 200 |
| 40 - 50 | 80 | Less than 50 | 280 |
| 50 - 60 | 50 | Less than 60 | 330 |
| 60 - 70 | 30 | Less than 70 | 360 |
| N = 360 |
Q5. The water bills (in rupees) of 32 houses in a certain street for the period 1.198 to 31.398 are given below:
56,43,32,38,56,24,68,85,52,47,35,58,63,74,27,84,69,35,44,75,55,30,54,65,45,67,95,72,43,65,35,69.
Tabulate the data and present the data as a cumulative frequency table using 70 - 79 as one of the class intervals.
Solution 5:
The minimum bill is Rs 24
The maximum bill is Rs 95
Range = Maximum bill - Minimum bill = 95 - 24 = 71
Given class interval is 70 - 79.So, class size = 79 - 70 = 9
Therefore number of classes = 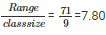
Number of classes = 8
The cumulative frequency distribution is as follows:
| Bills | No. of houses(frequency) | Cumulative frequency |
| 16 - 25 | 1 | 1 |
| 25 - 34 | 3 | 4 |
| 34 - 43 | 5 | 9 |
| 43 - 52 | 4 | 13 |
| 52 - 61 | 7 | 20 |
| 61 - 70 | 6 | 26 |
| 70 - 79 | 3 | 29 |
| 79 - 88 | 2 | 31 |
| 88 - 97 | 1 | 32 |
Q6.The number of books in different shelves of a library is as follows:
30, 32, 28, 24, 20, 25, 38, 37, 40, 45, 16, 20
19, 24, 27, 30, 32, 34, 35, 42, 27, 28, 19, 34
38, 39, 42, 29, 24, 27, 22, 29, 31, 19, 27, 25
28, 23, 24, 32, 34, 18, 27, 25, 37, 31, 24, 23
43, 32, 28, 31, 24, 23, 26, 36, 32, 29, 28, 21.
Prepare a cumulative frequency distribution table using 45 - 49 as the last class - interval.
Solution 6:
The minimum number of bookshelves is 16
and maximum number of bookshelves is 45
Range = Maximum book shelves - Minimum book shelves = 45 - 16 = 29
Given class interval is 45 - 49.So, class size = 49 - 45 = 4
Therefore number of classes = 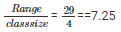
Number of classes = 8
The cumulative frequency distribution is as follows:
| No of books | No. of shelves(frequency) | Cumulative frequency |
| 13 - 17 | 1 | 1 |
| 17 - 21 | 6 | 7 |
| 21 - 25 | 11 | 18 |
| 25 - 29 | 15 | 33 |
| 29 - 33 | 12 | 45 |
| 33 - 37 | 5 | 50 |
| 37 - 41 | 6 | 56 |
| 41 - 45 | 3 | 59 |
| 45 - 49 | 1 | 60 |
Q7. Given below are the cumulative frequencies showing the weights of 685 students of a school. Prepare a frequency distribution table.
| Weight(in kg) | No. of students |
| Below 30 | 0 |
| Below 30 | 24 |
| Below 35 | 78 |
| Below 40 | 183 |
| Below 45 | 294 |
| Below 50 | 408 |
| Below 55 | 543 |
| Below 60 | 621 |
| Below 65 | 674 |
| Below 70 | 685 |
Solution 7:
| Weight(in kg) | No. of students | Class interval | frequency |
| Below 30 | 24 | 25 - 30 | 24 - 0 = 24 |
| Below 35 | 78 | 30 - 35 | 78 - 24 = 54 |
| Below 40 | 183 | 35 - 40 | 183 - 78 = 105 |
| Below 45 | 294 | 40 - 45 | 294 - 183 = 111 |
| Below 50 | 408 | 45 - 50 | 408 - 294 = 114 |
| Below 55 | 543 | 50 - 55 | 543 - 408 = 135 |
| Below 60 | 621 | 55 - 60 | 621 - 543 = 78 |
| Below 65 | 674 | 60 - 65 | 671 - 621 = 53 |
| Below 70 | 685 | 65 - 70 | 685 - 671 = 11 |
Q8. The following cumulative frequency distribution table shows the daily electricity consumption (in KW) of 40 factories in an industrial state.
| Consumption(in KW) | No. of factories |
| Below 240 | 1 |
| Below 270 | 4 |
| Below 300 | 8 |
| Below 330 | 24 |
| Below 360 | 33 |
| Below 390 | 38 |
| Below 420 | 40 |
(1) Represent this as a frequency distribution table.
(2)Prepare a cumulative frequency table.
Solution 8:
(1)
| Consumption(in KW) | No. of factories | Class interval | Frequency |
| Below 240 | 1 | 0 - 240 | 1 |
| Below 270 | 4 | 240 - 270 | 4 - 1 = 3 |
| Below 300 | 8 | 270 - 300 | 8 - 4 = 4 |
| Below 330 | 24 | 300 - 330 | 24 - 8 = 16 |
| Below 360 | 33 | 330 - 360 | 33 - 24 = 9 |
| Below 390 | 38 | 360 - 390 | 38 - 33 = 5 |
| Below 420 | 40 | 390 - 420 | 40 - 38 = 2 |
(2)
| Class interval | Frequency | Consumption(in KW) | No. of factories |
| 0 - 240 | 1 | More than 0 | 40 |
| 240 - 270 | 3 | More than 240 | 40 - 1 = 39 |
| 270 - 300 | 4 | More than 270 | 39 - 3 = 36 |
| 300 - 330 | 16 | More than 300 | 36 - 4 = 32 |
| 330 - 360 | 9 | More than 330 | 32 - 16 = 16 |
| 360 - 390 | 5 | More than 360 | 16 - 9 = 7 |
| 390 - 420 | 2 | More than 390 | 7 - 5 = 2 |
| More than 420 | 2 - 2 = 0 | ||
| N = 40 |
Q9. Given below is a cumulative frequency distribution table showing ages of the people living in a locality:
| Age in years | No. of years |
| Above 108 | 0 |
| Above 96 | 1 |
| Above 84 | 3 |
| Above 72 | 5 |
| Above 60 | 20 |
| Above 48 | 158 |
| Above 36 | 427 |
| Above 24 | 809 |
| Above 12 | 1026 |
| Above 0 | 1124 |
Prepare a frequency distribution table.
Solution 9:
| Age (in years) | No. of persons | Class interval | Frequency |
| Above 0 | 1124 | 0 - 12 | 1124 - 1026 = 98 |
| Above 12 | 1026 | 12 - 24 | 217 |
| Above 24 | 809 | 24 - 36 | 382 |
| Above 36 | 427 | 36 - 48 | 269 |
| Above 38 | 158 | 48 - 60 | 138 |
| Above 60 | 20 | 60 - 72 | 15 |
| Above 72 | 5 | 72 - 84 | 5 - 3 = 2 |
| Above 84 | 3 | 84 - 96 | 3 - 1 = 2 |
| Above 96 | 3 | 96 - 108 | 1 - 0 = 1 |
FAQs on Ex-22.2, Tabular Representation Of Statistical Data, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the importance of tabular representation of statistical data? |  |
| 2. How can I construct a frequency distribution table from raw data? |  |
| 3. How can I calculate the mean using a frequency distribution table? |  |
| 4. What is the difference between a class interval and class frequency? |  |
| 5. How can I calculate the median from a grouped frequency distribution table? |  |





















