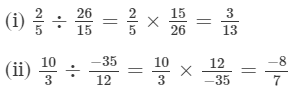RD Sharma Solutions (Ex -1. 5, 1.6, 1.7 & 1.8): Rational Numbers | RD Sharma Solutions for Class 8 Mathematics PDF Download
Exercise: 1.5
Question 1: Multiply:
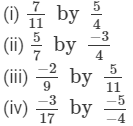
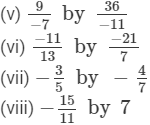
Answer :
(i) 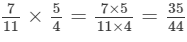
(ii) 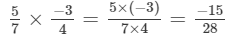
(iii) 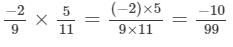
(iv) 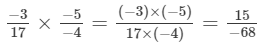
(v) 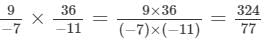
(vi) 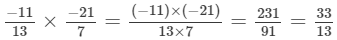
(vii) 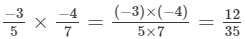
(viii) 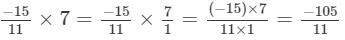
Question 2: Multiply:
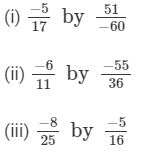
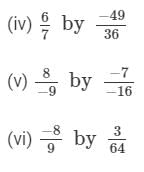
Answer :
(i) 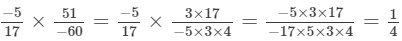
(ii) 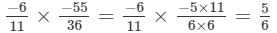
(iii) 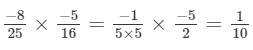
(iv) 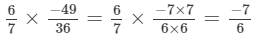
(v) 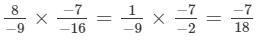
(vi) 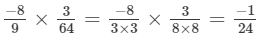
Question 3: Simplify each of the following and express the result as a rational number in standard form:
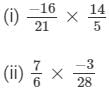
Answer :
(i) 
(ii) 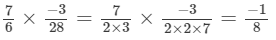
(iii) 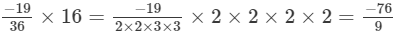
(iv) 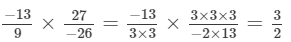
(v) 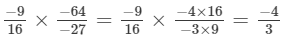
(vi) 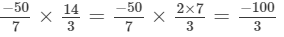
(vii) 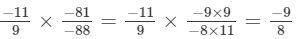
(viii) 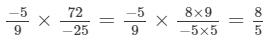
Question 4: Simplify:
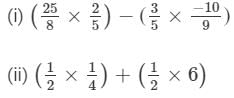
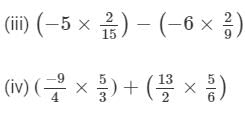
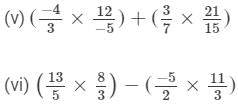
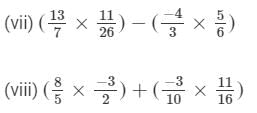
Answer :
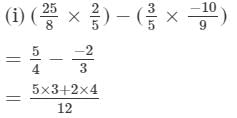
= 23/12
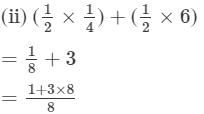
= 25/8
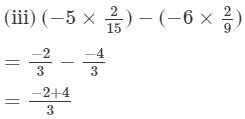
= 2/3
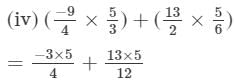
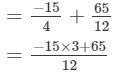
= 20/12 = 5/3
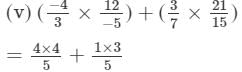
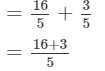
= 19/5
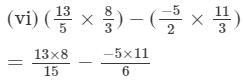
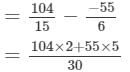
= 483/30
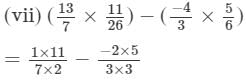
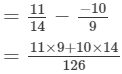
= 239/126
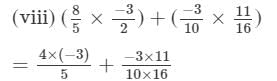
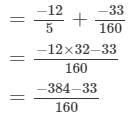
= -417/160
Question 5: Simplify:
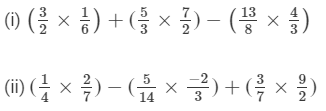
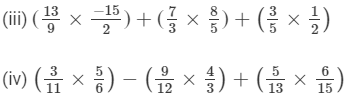
Answer :
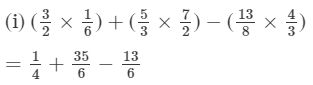
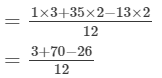
= 47/12
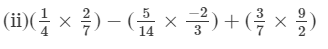
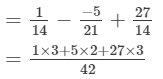
= 94/42 = 47/21
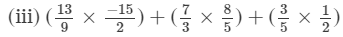
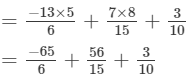
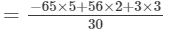
= -204/30 = -34/5
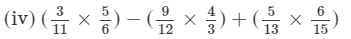
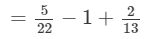
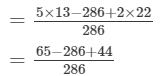
= -177/ 286
Exercise: 1.6
Question 1: Verify the property: x × y = y × x by taking:
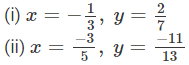
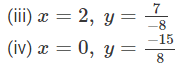
Answer :
We have to verify that x×y=y×x.
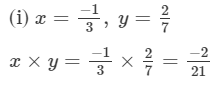
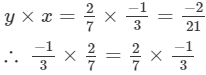
Hence verified.
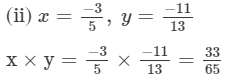
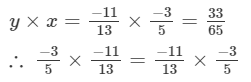
Hence verified.
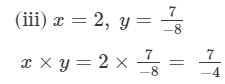
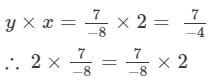
Hence verified.
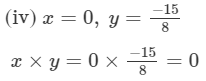
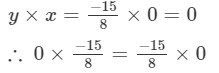
Hence verified.
Question 2: Verify the property: x × (y × z) = (x × y) × z by taking:
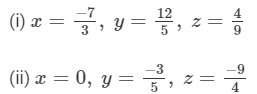
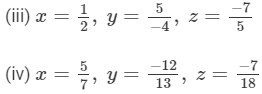
Answer :
We have to verify that x×(y×z)=(x×y)×z.
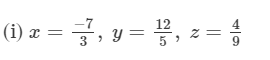
x×(y×z)=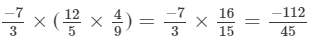
(x×y)×z= 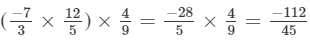
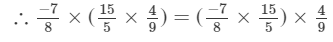
Hence verified.
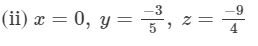
x×(y×z)= 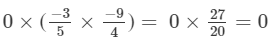
(x×y)×z= 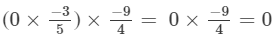
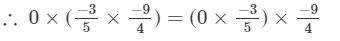
Hence verified.
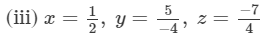
x×(y×z)= 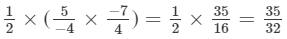
(x×y)×z= 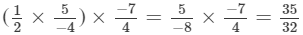
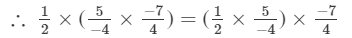
Hence verified.
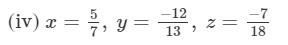
x×(y×z)= 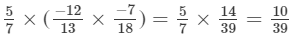
(x×y)×z= 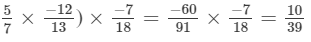
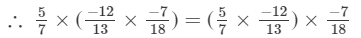
Hence verified.
Question 3: Verify the property: x × (y + z) = x × y + x × z by taking:
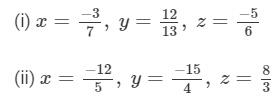
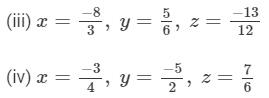
Answer :
We have to verify that x×(y+z)=x×y+x×z.
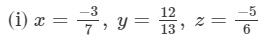
x×(y+z)= 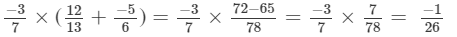
x×y+x×z= 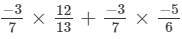
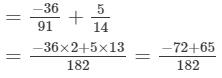
= -1/26
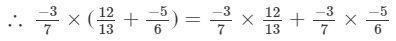
Hence verified.
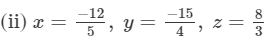
x×(y+z)= 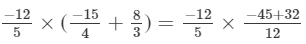 =
= 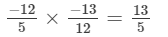
x×y+x×z= 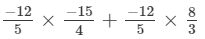
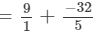
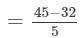
= 13/5
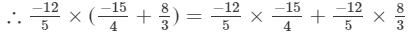
Hence verified.
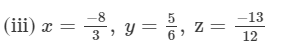
x×(y+z)= 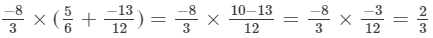
x×y+x×z= 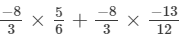
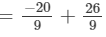
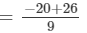
= 2/3
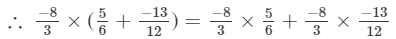
Hence verified .
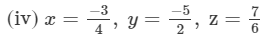
x×(y+z)= 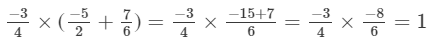
x×y+x×z= 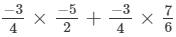
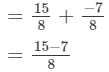
= 1
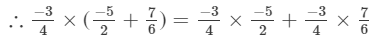
Hence verified.
Question 4: Use the distributivity of multiplication of rational numbers over their addition to simplify:
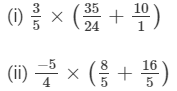
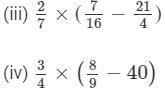
Answer :
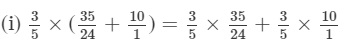
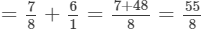
(ii) 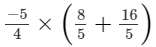
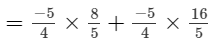
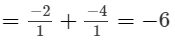
(iii) 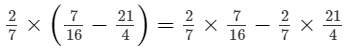
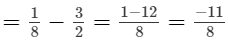
(iv) 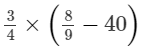
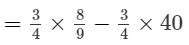
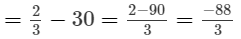
Question 5: Find the multiplicative inverse (reciprocal) of each of the following rational numbers:
(i) 9
(ii) −7
(iii) 12/5
(iv) −7/9
(v) −3/−5
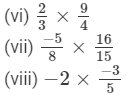
(ix) −1
(x) 0/3
(xi) 1
Answer :
(i) Multiplicative inverse (reciprocal) of 9 =1/9
(ii) Multiplicative inverse (reciprocal) of −7 = -1/7
(iii) Multiplicative inverse (reciprocal) of 12/5 = 5/12
(iv) Multiplicative inverse (reciprocal) of -7/9 = -9/7
(v) Multiplicative inverse (reciprocal) of -3/-5 = -5/-3 or 5/3
(vi) Multiplicative inverse (reciprocal) of 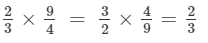
(vii) Multiplicative inverse (reciprocal) of 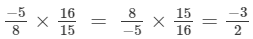
(viii) Multiplicative inverse (reciprocal) of 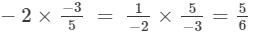
(ix) Multiplicative inverse (reciprocal) of 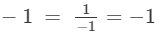
(x) Multiplicative inverse (reciprocal) of 0/3 = 3/0 = Undefined
(ix) Multiplicative inverse (reciprocal) of 1 = 1/1 = 1
Question 6: Name the property of multiplication of rational numbers illustrated by the following statements:
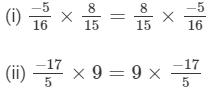
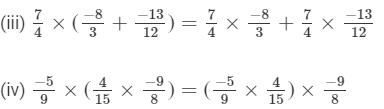
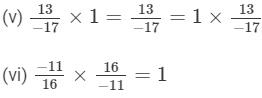
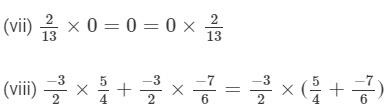
Answer :
(i) Commutative property
(ii) Commutative property
(iii) Distributivity of multiplication over addition
(iv) Associativity of multiplication
(v) Existence of identity for multiplication
(vi) Existence of multiplicative inverse
(vii) Multiplication by 0
(viii) Distributive property
Question 7: Fill in the blanks:
(i) The product of two positive rational numbers is always .....
(ii) The product of a positive rational number and a negative rational number is always .....
(iii) The product of two negative rational numbers is always .....
(iv) The reciprocal of a positive rational number is .....
(v) The reciprocal of a negative rational number is .....
(vi) Zero has ..... reciprocal.
(vii) The product of a rational number and its reciprocal is .....
(viii) The numbers ..... and ..... are their own reciprocals.
(ix) If a is reciprocal of b, then the reciprocal of b is .....
(x) The number 0 is ..... the reciprocal of any number.
(xi) Reciprocal of 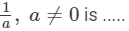
(xii) (17 × 12)−1 = 17−1 × .....
Answer :
(i) Positive
(ii) Negative
(iii) Positive
(iv) Positive
(v) Negative
(vi) No
(vii) 1
(viii) -1 and 1
(ix) a
(x) not
(xi) a
(xii) 12−112-1
Question 8: Fill in the blanks:
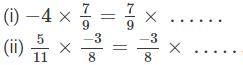
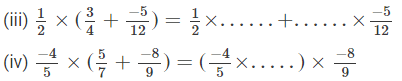
Answer :
(i) −4
x×y=y×x (commutativity)
(ii) 5/11
x×y=y×x (commutativity)
(iii) 3/4 ; 1/2
x×(y+z)=x×y+x×z (distributivity of multiplication over addition)
(iv) 5/7
x×(y×z)=(x×y)×z (associativity of multiplication )
Exercise: 1.7
Question 1: Divide:
(i) 1 by 1/2
(ii) 5 by −5/7(iii) −3/4 by 9/−16
(iv) −7/8 by −21/16
(v) 7/−4 by 63/64
(vi) 0 by −7/5
(vii) −3/4 by −6
(viii) 2/3 by −7/12
(ix) −4 by −3/5
(x) −3/13 by −4/65
Answer :
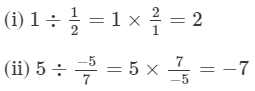
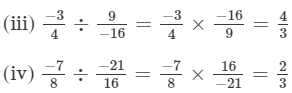
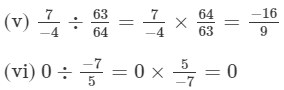
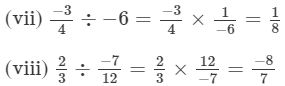
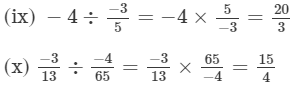
Question 2: Find the value and express as a rational number in standard form:
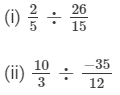
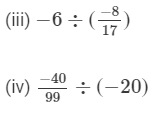
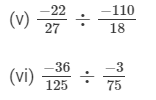
Answer 2:
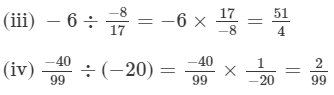
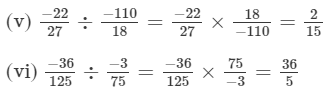
Question 3: The product of two rational numbers is 15. If one of the numbers is −10, find the other.
Answer 3:
Let the other number be x.
∴ x×(−10)=15
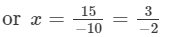
So, the other number is -3/2.
Question 4: The product of two rational numbers is -8/9. If one of the numbers is -4/15, find the other.
Answer 4: Let the other number be x.
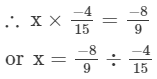
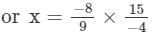
or x= 10/3
Thus, the other number is 10/3.
Question 5: By what number should we multiply -1/6-16 so that the product may be -23/9?
Answer 5: Let the number be x.
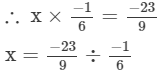
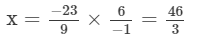
Therefore, the other number is 46/3.
Question 6: By what number should we multiply -15/28-1528 so that the product may be -5/7?-57?
Answer 6: Let the other number be x.
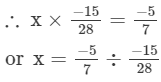
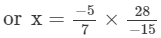
or x= 4/3
Thus, the other number is 4/3.
Question 7: By what number should we multiply -8/13 so that the product may be 24?
Answer 7: Let the number be x.
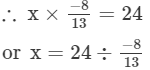
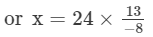
or x=−39
Thus, the number is −39.
Question 8: By what number should -3/434 be multiplied in order to produce 2/3?23?
Answer 8:
Let the other number that should be multiplied with -3/4 to produce2/3 be x.
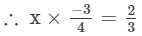
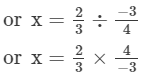
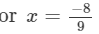
Thus, the number is -8/9.
Question 9: Find (x + y) ÷ (x − y), if
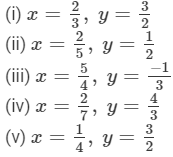
Answer 9:
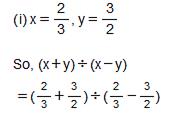
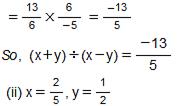
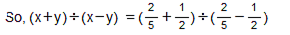
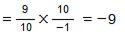
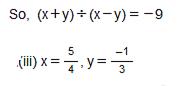
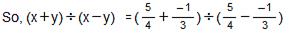
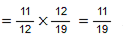
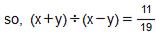
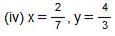
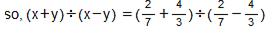
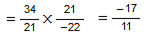
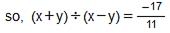
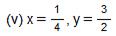
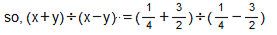
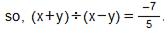
Question 10: The cost of 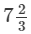 metres of rope is Rs
metres of rope is Rs 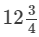 . Find its cost per metre.
. Find its cost per metre.
Answer 10: The cost of 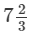 metres of rope is Rs
metres of rope is Rs 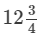 .∴Cost per metre =
.∴Cost per metre = 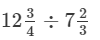
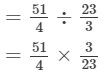
= 153/92
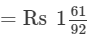
Question 11: The cost of 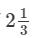 metres of cloth is Rs
metres of cloth is Rs 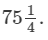 Find the cost of cloth per metre.
Find the cost of cloth per metre.
Answer 11: The cost of 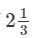 metres of cloth is Rs.
metres of cloth is Rs. 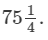 ∴ Cost per metre
∴ Cost per metre
=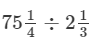
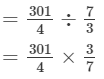 = 129/4
= 129/4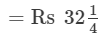 Thus,
Thus, 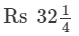 or Rs 32.25 is the cost of cloth per metre. Question 12: By what number should -33/16 be divided to get -11/4?
or Rs 32.25 is the cost of cloth per metre. Question 12: By what number should -33/16 be divided to get -11/4?
Answer 12: Let the number be x.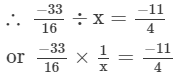
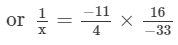
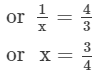 Thus, the number is 3/4.
Thus, the number is 3/4.
Question 13: Divide the sum of -13/5-135 and 12/7127 by the product of -31/7 and -1/2.-317 and -12.
Answer 13:

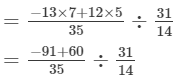
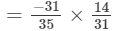
= -2/5
Question 14: Divide the sum of 65/12 and 12/7 by their difference.
Answer 14:
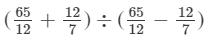
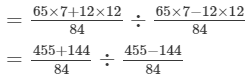
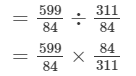
= 599/311
Question 15: If 24 trousers of equal size can be prepared in 54 metres of cloth, what length of cloth is required for each trouser?
Answer 15: Cloth needed to prepare 24 trousers=54 m
∴ Length of the cloth required for each trousers= 54÷24= 54/24 = 9/4 m = 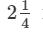 metres
metres
Exercise: 1.8
Question 1: Find a rational number between −3 and 1.
Answer 1: Rational number between −3 and 1 =
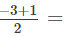 -2/2 = -1
-2/2 = -1
Question 2: Find any five rational numbers less than 2.
Answer 2:
We can write: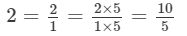
Integers less than 10 are 0, 1, 2, 3, 4, 5 ... 9.
Hence, five rational numbers less than 2 are 0/5, 1/5, 2/5, 3/5,and 4/5 .
Question 3: Find two rational numbers between −2/9 and 5/9.-29 and 59.
Answer 3:
Since both the fractions (−2/9 and 5/9) have the same denominator, the integers between the numerators(−2 and 5) are −1, 0, 1, 2, 3, 4.Hence, two rational numbers between −2/9 and 5/9 are 0/9 or 0 and 1/9.
Question 4: Find two rational numbers between 1/5 and 1/2.15 and 12
Answer 4: Rational number between1/5 and1/2 = 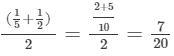
Rational number between 1/5 and7/20 =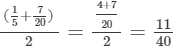
Therefore, two rational numbers between 1/5 and 1/2 are 7/20 and 11/40.
Question 5: Find ten rational numbers between 1/4 and 1/2.14 and 12.
Answer 5: The L.C.M of the denominators (2 and 4) is 4.
So, we can write 1/4 as it is.

As the integers between the numerators 1 and 2 of both the fractions are not sufficient, we will multiply the fractions by 20.
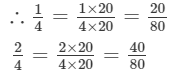
Between 20 and 40, there are 19 integers. They are 21, 22, 23, 24, 25, 26, 27....39, 40.
Thus, 21/40,22/40,23/40,24/40,25/40,...................38/40 and 39/40 are the fractions.We can take any 10 of these.
Question 6: Find ten rational numbers between -2/5 and1/2. and 12.
Answer 6:
L.C.M of the denominators (2 and 5) is 10.
We can write:
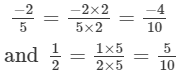
Since the integers between the numerators (−4 and 5 ) of both the fractions are not sufficient, we will multiply the ractions are not sufficient, we will multiply the fractions by 2.
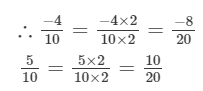
There are 17 integers between −8 and 10, which are −7,−6,−5,−4...................8, 9.These can be written as:
−7/20, −6/20, −5/20, −4/20, −3/20,................... 8/20 and 9/20
We can take any 10 of these.
Question 7: Find ten rational numbers Between 3/5 and 3/4.
Answer 7: The L.C.M of the denominators 5 and 4 of both the fractions is 20.We can write: 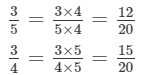
Since the integers between the numerators 12 and 15 are not sufficient, we will multiply both the fractions by 5.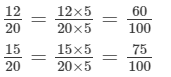
There are 14 integers between 60 and 75. They are 61, 62, 63.......73 and 74. Therefore, 60/100,61/100,62/100..........73/100 and74/100 are the 14 fractions. We can take any 10 of these.
FAQs on RD Sharma Solutions (Ex -1. 5, 1.6, 1.7 & 1.8): Rational Numbers - RD Sharma Solutions for Class 8 Mathematics
| 1. What are rational numbers? |  |
| 2. How do you determine if a number is rational? |  |
| 3. Can all real numbers be rational? |  |
| 4. How are rational numbers represented on a number line? |  |
| 5. How can rational numbers be used in real-life situations? |  |