RD Sharma Solutions Ex-12.1, Heron's Formula, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1 . Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm.
Solution:
Let the sides of the given triangle be a, b, c respectively.
So given,
a = 150 cm
b = 120 cm
c = 200 cm
By using Heron’s Formula
The area of the triangle = 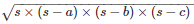
Semi perimeter of a triangle = s
2s = a + b + c
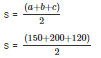
s = 235 cm
Therefore, area of the triangle 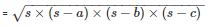
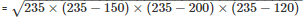
= 8966.56cm2
Q2. Find the area of a triangle whose sides are respectively 9 cm, 12 cm and 15 cm.
Solution:
Let the sides of the given triangle be a, b, c respectively.
So given,
a = 9 cm
b = 12 cm
c = 15 cm
By using Heron’s Formula
The area of the triangle = 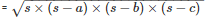
Semi perimeter of a triangle = s
2s = a + b + c
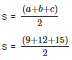
s = 18 cm
Therefore, area of the triangle = 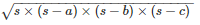
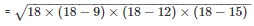
= 54cm2
Q3. Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm.
Solution:
Whenever we are given the measurements of all sides of a triangle, we basically look for Heron’s formula to find out the area of the triangle.
If we denote area of the triangle by A, then the area of a triangle having sides a, b, c and s as semi-perimeter is given by:
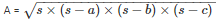
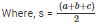
We are given:
a = 18 cm
b = 10 cm, and perimeter = 42 cm
We know that perimeter = 2s,
So, 2s = 42
Therefore, s = 21 cm
We know that, 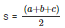
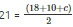
42 = 28 + c
c = 14 cm
So the area of the triangle is:
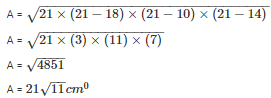
Q4 . In a triangle ABC, AB = 15cm, BC = 13cm and AC = 14cm. Find the area of triangle ABC and hence its altitude on AC.
Solution:
Let the sides of the given triangle be AB = a, BC = b, AC = c respectively.
So given,
a = 15 cm
b = 13 cm
c = 14 cm
By using Heron’s Formula
The area of the triangle =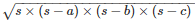
Semi perimeter of a triangle= 2s
2s = a + b + c
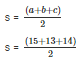
s = 21 cm
Therefore, area of the triangle 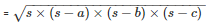

= 84cm2
BE is a perpendicular on AC
Now, area of triangle = 84cm2
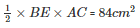
BE = 12cm
The length of BE is 12 cm
Q5 . The perimeter of a triangular field is 540 m and its sides are in the ratio 25:17:12. Find the area of triangle.
Solution:
Let the sides of the given triangle be a = 25x, b = 17x, c = 12x respectively,
So,
a = 25x cm
b = 17x cm
c = 12x cm
Given Perimeter = 540 cm
2s = a + b + c
a + b + c = 540 cm
25x + 17x + 12x = 540 cm
54x = 540 cm
x = 10 cm
Therefore, the sides of a triangle are
a = 250 cm
b = 170 cm
c = 120 cm
Now, Semi perimeter 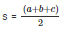
= 540/2
= 270 cm
By using Heron’s Formula
The area of the triangle 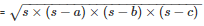
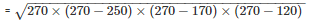
= 9000cm2
Therefore, the area of the triangle is 9000cm2
Q6. The perimeter of a triangle is 300 m. If its sides are in the ratio of 3: 5: 7. Find the area of the triangle.
Solution:
Given the perimeter of a triangle is 300 m and the sides are in a ratio of 3: 5: 7
Let the sides a, b, c of a triangle be 3x, 5x, 7x respectively
So, the perimeter = 2s = a + b + c
200 = a + b + c
300 = 3x + 5x + 7x
300 = 15x
Therefore, x = 20 m
So, the respective sides are
a = 60 m
b = 100 m
c = 140 m
Now, semi perimeter 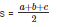
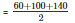
= 150 m
By using Heron’s Formula
The area of a triangle 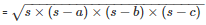

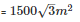
Thus, the area of a triangle is 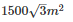
Q7. The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
Solution:
Given,
In a triangle ABC, a = 78 dm = AB, b = 50 dm = BC
Now, Perimeter = 240 dm
Then, AB + BC + AC = 240 dm
78 + 50 + AC = 240
AC = 240-(78+50)
AC = 112 dm = c
Now, 2s = a + b + c
2s = 78 + 50 + 112
s = 120 dm
Area of a triangle ABC 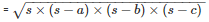
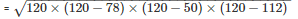
= 1680dm2
Let AD be a perpendicular on BC
Area of the triangle ABC = 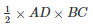
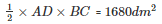
AD = 67.2 dm
Q8. A triangle has sides 35 cm, 54 cm, 61 cm long. Find its area. Also, find the smallest of its altitudes?
Solution:
Given,
The sides of the triangle are
a = 35 cm
b = 54 cm
c = 61 cm
Perimeter 2s = a + b + c
2s = 35 + 54 + 61 cm
Semi perimeter s = 75 cm
By using Heron’s Formula,
Area of the triangle 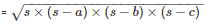
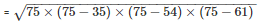
= 939.14cm2
The altitude will be smallest provided the side corresponding to this altitude is longest.
The longest side = 61 cm
Area of the triangle 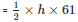
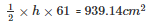
h = 30.79cm
Hence the length of the smallest altitude is 30.79cm
Q9.The lengths of the sides of a triangle are in a ratio of 3 : 4 : 5 and its perimeter is 144 cm. Find the area of the triangle and the height corresponding to the longest side?
Solution:
Given the perimeter of a triangle is 160m and the sides are in a ratio of 3 : 4 : 5
Let the sides a, b, c of a triangle be 3x, 4x, 5x respectively
So, the perimeter = 2s = a + b + c
144 = a + b + c
144 = 3x+ 4x+ 5x
Therefore, x = 12cm
So, the respective sides are
a = 36cm
b = 48cm
c = 60cm
Now, semi perimeter 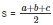
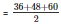
= 72 cm
By using Heron’s Formula
The area of a triangle 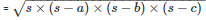
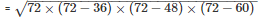
= 864cm2
Thus, the area of a triangle is 864cm2
The altitude will be smallest provided the side corresponding to this altitude is longest.
The longest side = 60 cm
Area of the triangle 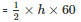
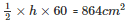
h = 28.8 cm
Hence the length of the smallest altitude is 28.8 cm
Q10. The perimeter of an isosceles triangle is 42 cm and its base is 3/2 times each of the equal side. Find the length of each of the triangle, area of the triangle and the height of the triangle.
Solution:
Let ‘x’ be the length of two equal sides,
Therefore the base 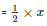
Let the sides a, b, c of a triangle be 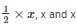 respectively
respectively
So, the perimeter = 2s = a + b + c
42 = a + b + c
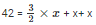
Therefore, x = 12 cm
So, the respective sides are
a = 12 cm
b = 12 cm
c = 18 cm
Now, semi perimeter 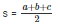
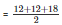
= 21 cm
By using Heron’s Formula
The area of a triangle 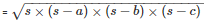
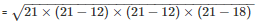
= 71.42cm2
Thus, the area of a triangle is 71.42cm2
The altitude will be smallest provided the side corresponding to this altitude is longest.
The longest side = 18 cm
Area of the triangle 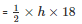
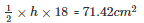
h = 7.93 cm
Hence the length of the smallest altitude is 7.93 cm
Q11. Find the area of the shaded region in fig. below
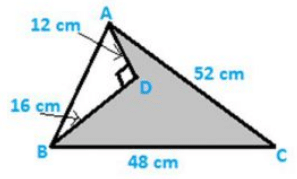
Solution:
Area of the shaded region = Area of ΔABC−Area of ΔADB
Now in triangle ADB
AB2 = AD2+BD2………(i)
Given, AD = 12 cm, BD =16 cm
Substituting the value of AD and BD in eq (i), we get
AB2 = 122+162
= 400cm2
AB = 20 cm
Now, area of a triangle 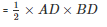
= 96cm2
Now in triangle ABC,
The area of a triangle 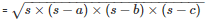
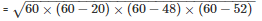
= 480cm2
Thus, the area of a triangle is 480cm2
Area of shaded region = Area of triangle ABC – Area of triangle ADB
= (480 – 96) cm2
= 384 cm2
Area of shaded region = 384 cm2
FAQs on RD Sharma Solutions Ex-12.1, Heron's Formula, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What is Heron's formula and how is it used to find the area of a triangle? |  |
| 2. How do you calculate the semi-perimeter of a triangle? |  |
| 3. Can Heron's formula be used for any type of triangle? |  |
| 4. Can Heron's formula be used to find the area of a triangle if only the side lengths are given? |  |
| 5. Are there any other formulas to find the area of a triangle apart from Heron's formula? |  |
















