Measurement Class 4 Notes Maths

What is Measurement?
Measurement is like giving numbers to things we can see or feel. It helps us understand how big or small something is, how heavy or light it is, or how long or short it is.

For example, when you say your pencil is 15 centimeters long, or your backpack weighs 3 kilograms, you're using measurements to describe those things. So, measurement is just a way to use numbers to describe stuff in the world around us.
Length
The standard unit used to measure length in almost all countries is metre written as m.
Smaller lengths are measured in centimetres written as cm.
What is the relation between centimetres and metres?
Observe carefully the metre scale! It has 100 divisions. Each division is equal to one centimetre.
It has 100 divisions. Each division is equal to one centimetre.
∴ 1 m = 100 cm
Can you measure the distance between Agra and Delhi easily in metres?No!
To measure greater lengths, we use another unit of length called a kilometre, written as km.
Therefore, 1 km = 1000 m
Measuring Lengths
To measure the length of an object in centimetres, you can use a centimetre ruler. The picture above shows a 15 cm ruler.
The picture above shows a 15 cm ruler.
To measure the length of your pencil using a 15 cm ruler, place the pencil along the ruler in such a manner that its one end coincides or matches with the 0 mark of the ruler. From the above figure, we observe that one end of the pencil is at 0 mark and the other end, i.e., the tip of the pencil is at the 10 cm mark. This shows that the length of the pencil is 10 cm.
From the above figure, we observe that one end of the pencil is at 0 mark and the other end, i.e., the tip of the pencil is at the 10 cm mark. This shows that the length of the pencil is 10 cm.
Similarly, to measure the length of a given line segment, we place the ruler along the line segment such that one endpoint coincides with the zero mark of the ruler. The marking on the ruler at the other end shows the length of the line segment. From the above figure, we can see that the length of the given line segment is 7 cm.
From the above figure, we can see that the length of the given line segment is 7 cm. Each centimetre is divided into 10 equal parts. From the above figure, we can see that for the given line segment, one endpoint is at mark 0 and the other endpoint is at the 7th division after the 8 cm mark. The length of the given line segment is, therefore,
Each centimetre is divided into 10 equal parts. From the above figure, we can see that for the given line segment, one endpoint is at mark 0 and the other endpoint is at the 7th division after the 8 cm mark. The length of the given line segment is, therefore,
Conversion of Metric units of Length
1. To convert metres to centimetres, multiply by 100.
Example 1: Convert 8 m and 52 m into centimetres.
Sol: Because 1 m = 100 cm,
Therefore, 8 m = 8 × 100 cm = 800 cm;
52 m = 52 × 100 cm = 5200 cm.
Edurev Tips:
- 1 m = 100 cm,
- 1 km = 1000 m.
Example 2: Express 5 m 64 cm and 22 m 8 cm as centimetres.
Sol: 5 m 64 cm = 5 m and 64 cm = 5 × 100 cm + 64 cm = 500 cm + 64 cm = 564 cm.
22 m 8 cm = 22 m and 8 cm = 22 × 100 cm + 8 cm = 2200 cm + 8 cm = 2208 cm.
Edurev Tips:
- To convert higher units of length to lower units, we multiply.
- To convert lower units of length to higher units, we divide.
2. To convert centimetres to metres, divide by 100.
Example 3: Convert 700 cm into metres.
Sol:
Therefore, 700 cm = (700 ÷ 100) m = 7 m.
Example 4: Convert 265 cm and 2560 cm into metres and centimetres.
Sol: 265 cm = 200 cm + 65 cm = (200 ÷ 100) m + 65 cm = 2 m 65 cm.
2560 cm = 2500 cm + 60 cm = (2500 ÷ 100) m + 60 cm = 25 m 60 cm.
3. To convert kilometres to metres, multiply by 1000.
Example 5: Convert the following into metres.
(a) 9 km
(b) 27 km 532 m
Sol: (a) 9 km = 9 × 1000 m = 9000 m. (∵ 1 km = 1000 m)
(b) 27 km 532 m = 27 km and 532 m = 27 × 1000 m + 532 m = 27000 m + 532 m = 27532 m.
4. To convert metres to kilometres, divide by 1000.
Example 6: Convert 56000 m into km.
Sol: 56000 m = (56000 ÷ 1000) km = 56 km.
Example 7: Convert 8606 m into kilometres and metres.
Sol: 8606 m = 8000 m + 606 m
= (8000 ÷ 1000) km + 606 m
= 8 km 606 m.
Addition and Subtraction of Length
Addition of Kilometres, Metres and Centimetres
Addition of metric units is done in the same way as we do for whole numbers. There are two ways of adding metric units.
- You can convert to smaller units and then add them.
- You can add the units by writing them in different columns.
Example 8: Add 32 m 76 cm and 39 m 27 cm.
Sol: Arranging m and cm vertically in columns, we have
Thus, the sum of 32 m 76 cm and 39 m 27 cm is 72 m 3 cm.
Working:
Think:
76 cm + 27 cm = 103 cm
103 cm = 100 cm + 3 cm
= 1 m 3 cm
Example 9: Find the sum of 14 km 295 m and 46 km 707 m.
Sol: Arranging m and cm vertically in columns, we have
Thus, 14 km 295 m + 46 km 707 m = 61 km 2 m.
Working:
Think:
295 m + 707 m = 1002 m
1002 m = 1000 m + 2 m
= 1 km 2 m
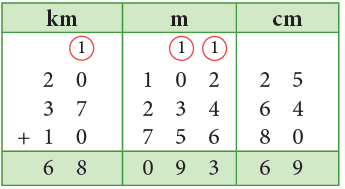
Example 10: Add 20 km 102 m 25 cm, 37 km 234 m 64 cm and 10 km 756 m 80 cm.
Sol: Arranging km, m and cm vertically in columns, we have
Thus, 20 km 102 m 25 cm + 37 km 234 m 64 cm + 10 km 756 m 80 cm
= 68 km 93 m 69 cm.
Think:
25 cm + 64 cm + 80 cm
= 169 cm = 1 m 69 cm
Carry 1 to the m column.
1 m + 102 m + 234 m + 756 m
= 1093 m = 1 km 93 m
Carry 1 to the km column.
Subtraction of Metric Units
Subtraction of metric units is done in the same way as we do for whole numbers.
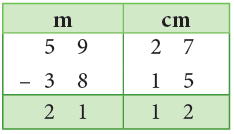
Example 11: Subtract 38 m 15 cm from 59 m 27 cm.
Sol:Arranging in columns, we have
Thus, the difference of 59 m 27 cm and 38 m 15 cm is 21 m 12 cm.
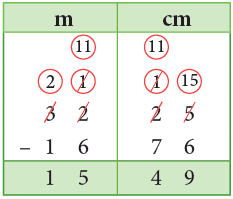
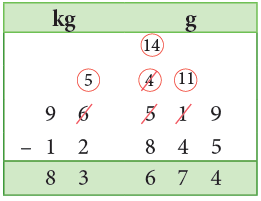
Example 12: Subtract 16 m 76 cm from 32 m 25 cm.
Sol: Arranging in columns, we have
Thus, 32 m 25 cm – 16 m 76 cm = 15 m 49 cm.
Think:
Subtract centimetres: 76 cm cannot be subtracted from 25 cm, so we borrow 1 m from the metres column.
Now, we have
1 m 25 cm = 100 cm + 25 cm = 125 cm. Subtract 76 cm from 125 cm.
125 cm – 76 cm = 49 cm
Subtract metres: 32 m – 1 m = 31 m
Now, 31 m – 16 m = 15 m.
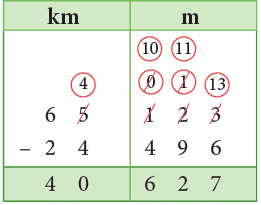
Example 13: Subtract 24 km 496 m from 65 km 123 m.
Sol: Arranging in columns, we have
Thus, 65 km 123 m – 24 km 496 m = 40 km 627 m.
Think:
Subtract metres: We see that 496 cannot be subtracted from 123. So, we borrow 1 km from the km column.
1 km + 123 m = 1000 m + 123 m = 1123 m.
Now, subtract 496 m from 1123 m.
1123 m – 496 m = 627 m
In kilometres column (65 – 1) km = 64 km.
Now, 64 km – 24 km = 40 km.
Problems Based on Real Life Situations
Example 14: Prachi cycled 2 km 250 m on Saturday and 3 km 980 m on Sunday. How much distance did she cycle altogether on the two days?
Sol: Arranging in columns, we have
Thus, Prachi cycled 6 km 230 m.
Example 15: Mohini has 5 m 20 cm of cloth. She only needs 2 m 50 cm of cloth to make a dress. How much cloth will remain after making the dress?
Sol: Subtract 2 m 50 cm from 5 cm 20 cm.
Thus, 2 m 70 cm cloth will remain after making the dress.
Estimate of Length
To estimate the length of an object, you relate it to the length of some objects that you know.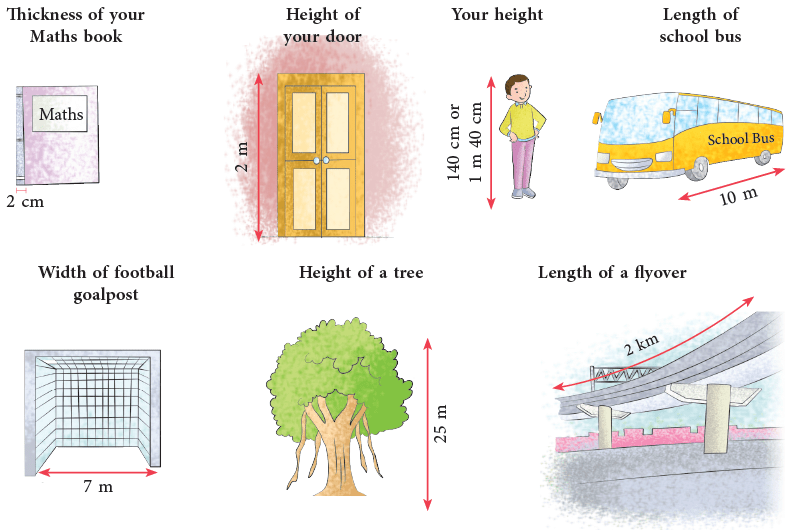
Measures of Weight (Kilogram and Gram)
The standard units of weight in most of the countries are kilograms and grams.
Kilogram is used to measure heavy weights such as the weight of a person, your school bag, etc., whereas gram is used to measure light weights, such as the weight of a feather, a chocolate, etc.
Kilogram is written as kg and gram is written as g in short form.
or one-thousandth of 1 kg.
The standard weights made of iron are:
Edurev Tips:
When you go to buy vegetables, fruits or sweets, you see the shopkeeper weighing the needed quantity with the help of a common balance.
Gram weights can be smaller too. They are made of brass and are generally used by goldsmiths. Weights are kept on one pan and the objects to be weighed on the other. When both the pans are at the same level, the weights are equal.
Weights are kept on one pan and the objects to be weighed on the other. When both the pans are at the same level, the weights are equal.
The pan with the heavier weight moves down, whereas the pan with the lighter weight moves up. The following example shows the weights in both the pans.
Can you determine how much weight has to be added to the lighter pan, so as to balance the pans?

Conversions of Metric units of Weight
Conversion of kg to g and g to kg is done in the same manner as you did for km and m.
- To convert kg to g, multiply by 1000.
- To convert g to kg, divide by 1000.
Example 16: Express the following in grams.
(a) 8 kg
(b) 47 kg
(c) 6 kg 325 g
(d) 17 kg 85 g
Sol: (a) 8 kg = 8 × 1000 g = 8000 g.
(b) 47 kg = 47 × 1000 g = 47000 g.
(c) 6 kg 325 g = 6 × 1000 g + 325 g = 6000 g + 325 g = 6325 g.
(d) 17 kg 85 g = 17 × 1000 g + 85 g = 17000 g + 85 g = 17085 g.
Example 17: Express the following in kilograms and grams.
(a) 7000 g
(b) 5538 g
(c) 6209 g
(d) 4019 g
Sol: (a) 7000 g = (7000 ÷ 1000) kg = 7 kg.
(b) 5538 g = 5000 g + 538 g = (5000 ÷ 1000) kg + 538 g = 5 kg 538 g.
(c) 6209 g = 6000 g + 209 g = (6000 ÷ 1000) kg + 209 g = 6 kg 209 g.
(d) 4019 g = 4000 g + 19 g = (4000 ÷ 1000) kg + 19 g = 4 kg 19 g.
Addition and Subtraction of Weights
Arrange the weights vertically in two columns and then add them separately as we did with km and m.
Example 18: Add 23 kg 521 g, 53 kg 293 g and 18 kg 509 g.
Sol: Arranging in columns, we have
Thus, the sum is 95 kg 323 g.
Think:
521 g + 293 g + 509 g
= 1323 g = 1 kg 323 g
Carry 1 to the kg column.
Example 19: Subtract 12 kg 845 g from 96 kg 519 g.
Sol: Arranging in columns, we have
Thus, the difference is 83 kg 674 g.
Think:
845 g cannot be subtracted from 519 g, so we borrow 1 kg = 1000 g, from the kg column.
Example 20: Mr Verma weighs 75 kg 240 g, Mrs Verma weighs 60 kg 960 g and their daughter Mona weighs 35 kg 250 g.
(a) What is the sum of their weights?
(b) How much more does Mrs Verma weigh than her daughter?
Sol: (a) Add the given weights.
Thus, the sum of the weights of Mr Verma’s family = 171 kg 450 g.
(b) 60 kg 960 g – 35 kg 250 g = 25 kg 710 g.
Thus, Mrs Verma weighs 25 kg 710 g more than her daughter.
Estimate of Weight
To estimate the weight of a given object, you should have an idea of the weights of some common objects around you. A 200-rupee note has a weight of about 1 g and about 10 packets of chips costing ₹ 20 each have a weight of about 1 kg.
Measures of Capacity (Litre and Millilitre)
Capacity is the amount of water, milk, oil or any other liquid that a container (e.g. bottle) can hold. The standard units for measuring capacity are litres written as L and millilitres written as mL.
Edurev Tips: Milli means one-thousandth of litre i.e., 1 / 1000
You can see the capacity written on the container, be it a can of juice or a bottle of medicine. Some of the standard containers marked with standard units to measure the capacity of liquids are shown here.
Some of the standard containers marked with standard units to measure the capacity of liquids are shown here.
These containers are generally used for measuring milk: These containers are generally used for measuring petrol and oil:
These containers are generally used for measuring petrol and oil: From the pictures given above, you can now understand that smaller capacities are measured in millilitres and the larger ones in litres.
From the pictures given above, you can now understand that smaller capacities are measured in millilitres and the larger ones in litres.
Estimate of Capacity
To help estimate the capacity, keep in mind the capacity of some commonly used things.

Conversion of Metric units of Capacity
Conversion of litre to millilitre and millilitre to litre is done in the same manner, as you did for kilogram and gram.
Example 21: Express the following in millilitres.
(a) 2 L
(b) 6 L 480 mL
Sol: (a) 2 L = 2 × 1000 mL = 2000 mL.
(b) 6 L 480 mL = 6 × 1000 mL + 480 mL
= 6000 mL + 480 mL = 6480 mL.
Example 22: Express the following in litres and millilitres.
(a) 9000 mL
(b) 5450 mL
Sol: (a) 9000 mL = (9000 ÷ 1000) L = 9 L.
(b) 5450 mL = 5000 mL + 450 mL
= (5000 ÷ 1000) L + 450 mL = 5 L 450 mL.
Addition and Subtraction of Capacity
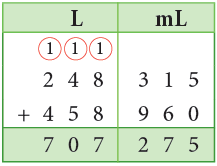
Example 23: Add 248 L 315 mL and 458 L 960 mL.
Sol: Arranging vertically in two columns of L and mL.
Thus, the sum is 707 L 275 mL.
1. Add the millilitres.
315 mL + 960 mL = 1275 mL
1275 mL = 1000 mL + 275 mL = 1 L + 275 mL
Carry 1 L to the litre column.
2. Add the litres.
248 L + 458 L + 1 L = 707 L
Example 24: Subtract 83 L 448 mL from 95 L 368 mL.
Sol: Arranging vertically in two columns of L and mL.
Thus, the difference is 11 L 920 mL.
1. Subtract the millilitres.
We cannot subtract 448 mL from 368 mL.
Borrow 1 L from 95 L.
1 L + 368 mL = 1000 mL + 368 mL = 1368 mL
1368 mL – 448 mL = 920 mL
2. Subtract the litres.
94 L – 83 L = 11 L
Table of Units

|
30 videos|110 docs|30 tests
|
FAQs on Measurement Class 4 Notes Maths
| 1. What is the definition of measurement in mathematics? |  |
| 2. How do you convert metric units of length? |  |
| 3. How can I add or subtract lengths in measurement? |  |
| 4. What are common measures of weight in the metric system? |  |
| 5. What is the difference between liters and milliliters in measuring capacity? |  |