RD Sharma Solutions Ex-12.2, (Part -1), Heron's Formula, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1. Find the area of the quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Solution:
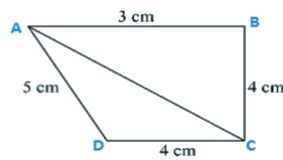
For triangle ABC
AC2 = BC2+AB2
25 = 9 + 16
So, triangle ABC is a right angle triangle right angled at point R
Area of triangle ABC = 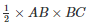
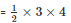
= 6 cm2
From triangle CAD
Perimeter = 2s = AC + CD + DA
2s = 5 cm+ 4 cm+ 5 cm
2s = 14 cm
s = 7 cm
By using Heron’s Formula
Area of the triangle CAD 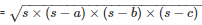
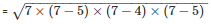
= 9.16cm2
Area of ABCD = Area of ABC + Area of CAD
= (6+9.16) cm2
= 15.16cm2
Q2. The sides of a quadrilateral field, taken in order are 26 m, 27 m, 7 m, 24 m respectively. The angle contained by the last two sides is a right angle. Find its area.
Solution:
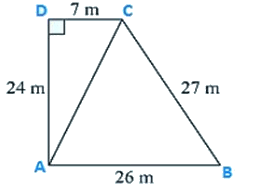
Here the length of the sides of the quadrilateral is given as
AB = 26 m, BC = 27 m, CD = 7 m, DA = 24 m
Diagonal AC is joined.
Now, in triangle ADC
By applying Pythagoras theorem
AC2 = AD2+CD2
AC2 = 142+72
AC = 25 m
Now area of triangle ABC
Perimeter = 2s = AB + BC + CA
2s = 26 m + 27 m + 25 m
s = 39 m
By using Heron’s Formula
The area of a triangle 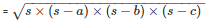
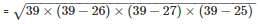
= 291.84m2
Thus, the area of a triangle is 291.84m2
Now for area of triangle ADC
Perimeter = 2s = AD + CD + AC
= 25 m + 24 m + 7 m
s = 28 m
By using Heron’s Formula
The area of a triangle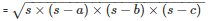
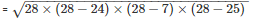
= 84m2
Thus, the area of a triangle is 84m2
Therefore, Area of rectangular field ABCD
= Area of triangle ABC + Area of triangle ADC
= 291.84 + 84
= 375.8 m2
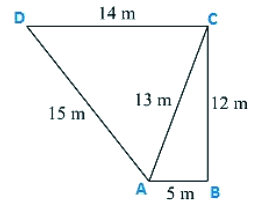
Q3. The sides of a quadrilateral, taken in order as 5 m, 12 m, 14 m, 15 m respectively, and the angle contained by first two sides is a right angle. Find its area.
Solution:
Given that the sides of the quadrilateral are
AB = 5 m, BC = 12 m, CD =14 m and DA = 15 m
Join AC
Now area of triangle ABC 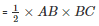
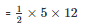
= 30 m2
In triangle ABC, By applying Pythagoras theorem
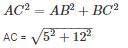
AC = 13 m
Now in triangle ADC,
Perimeter = 2s = AD + DC + AC
2s = 15 m +14 m +13 m
s = 21 m
By using Heron’s Formula,
Area of the triangle PSR = 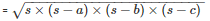
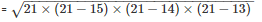
= 84m2
Area of quadrilateral ABCD = Area of triangle ABC + Area of triangle ADC
= (30 + 84) m2
= 114m2
Q4. A park in the shape of a quadrilateral ABCD, has angle C = 900, AB = 9 m, BC = 12 m, CD = 5 m, AD = 8 m. How much area does it occupy?
Solution:
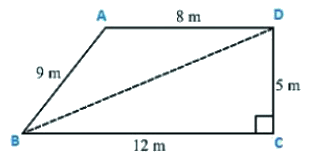
Given sides of a quadrilateral are AB = 9 m, BC = 12 m, CD = 5 m, DA = 8 m.
Let us join BD
In triangle BCD , apply Pythagoras theorem
BD2 = BC2+CD2
BD2 = 122+52
BD = 13 m
Area of triangle BCD = 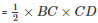
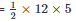
= 30 m2
Now, in triangle ABD
Perimeter = 2s = 9 m + 8m + 13m
s = 15 m
By using Heron’s Formula,
Area of the triangle ABD = 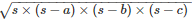
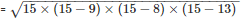
= 35.49m2
Area of quadrilateral ABCD = Area of triangle ABD + Area of triangle BCD
= (35.496 + 30) m2
= 65.5m2.
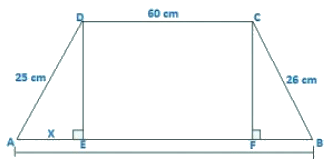
Q5. Two parallel sides of a trapezium are 60 m and 77 m and the other sides are 25 m and 26 m. Find the area of the trapezium?
Solution:
Given,
Two parallel sides of trapezium are AB = 77 m and CD = 60 m
The other two parallel sides of trapezium are BC = 26 m, AD = 25m
Join AE and CF
DE is perpendicular to AB and also, CF is perpendicular to AB
Therefore, DC = EF = 60 m
Let AE = x
So, BF = 77 – 60 – x
BF = 17 – x
In triangle ADE,
By using Pythagoras theorem,
DE2 = AD2−AE2
DE2 = 252−x2
In triangle BCF,
By using Pythagoras theorem,
CF2 = BC2−BF2
CF2 = 262−(17−x)2
Here, DE = CF
So, DE2 = CF2
252−x2 = 262−(17−x)2
252−x2 = 262−(172−34x+x2)
252−x2 = 262−172+34x+x2
252 = 262−172+34x
x = 7
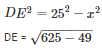
DE = 24 m
Area of trapezium 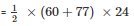
Area of trapezium = 1644m2
Q6. Find the area of a rhombus whose perimeter is 80 m and one of whose diagonal is 24 m.
Solution:
Given,
Perimeter of a rhombus = 80 m
As we know,
Perimeter of a rhombus = 4×side = 4×a
4×a = 80 m
a = 20 m
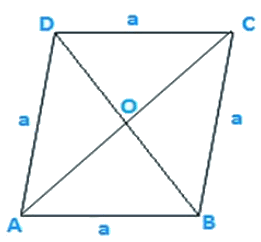
Let AC = 24 m
Therefore OA 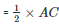
OA = 12 m
In triangle AOB
OB2 = AB2−OA2
OB2 = 202−122
OB = 16 m
Also, OB = OD because diagonal of rhombus bisect each other at 90∘
Therefore, BD = 2 OB = 2 x 16 = 32 m
Area of rhombus 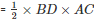
Area of rhombus 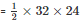
Area of rhombus = 384 m2
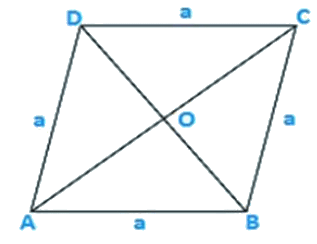
Q7. A rhombus sheet, whose perimeter is 32 m and whose diagonal is 10 m long, is painted on both the sides at the rate of Rs 5 per meter square. Find the cost of painting.
Solution:
Given that,
Perimeter of a rhombus = 32 m
We know that,
Perimeter of a rhombus = 4×side
4×side = 32 m
4×a = 32 m
a = 8 m
Let AC = 10 m
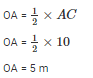
By using Pythagoras theorem
OB2 = AB2–OA2
OB2 = 82–52
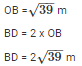
Area of the sheet 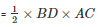
Area of the sheet 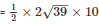
Therefore, cost of printing on both sides at the rate of Rs. 5 per m2
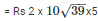
= Rs. 625
FAQs on RD Sharma Solutions Ex-12.2, (Part -1), Heron's Formula, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What is Heron's formula? |  |
| 2. How is Heron's formula derived? |  |
| 3. Can Heron's formula be used for all types of triangles? |  |
| 4. Are there any limitations to using Heron's formula? |  |
| 5. How is Heron's formula useful in real-life applications? |  |
















