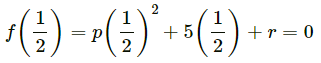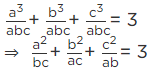NCERT Exemplar Solutions: Polynomials - 2 | Mathematics for Grade 9 PDF Download
Exercise 2.4
Q1. If the polynomials az3 + 4 z2 + 3 z – 4 and z3 – 4 z + a leave the same remainder when divided by z – 3, find the value of a.
Solution: Let p1(z) = az3 + 4z2 + 3z – 4 and p2(z) = z3 – 4z + 0
When we divide p1(z) by z – 3, then we get the remainder p,(3).
Now, p1(3) = a(3)3 + 4(3)2 + 3(3) – 4
= 27a + 36 + 9 – 4
= 27a + 41
When we divide p2(z) by z – 3 then
we get the remainder p2(3).
Now, p2(3) = (3)3 – 4(3) + a
= 27 – 12 + a
= 15 + a
Both the remainders are same.
p1(3) = p2(3)
27a + 41 = 15 + a
27a – a = 15 – 41 .
26a = 26a = – 1
Q2. The polynomial p(x) = x4 – 2x3 + 3x2 – ax + 3a – 7 when divided by x + 1 leaves the remainder 19. Find the values of a. Also find the remainder when p(x) is divided by x + 2.
Solution: Given, p(x) = x4 – 2x3 + 3x2 – ax + 3a – 7
When we divide p(x) by x + 1, then we get the remainder p(– 1).
Now, p(– 1) = (– 1)4 – 2(– 1)3 + 3(– 1)2 – a(– 1) + 3a – 7
= 1 + 2 + 3 + a + 3a – 7
= 4a – 1
p(– 1) = 19
⇒ 4a – 1 = 19
⇒ 4a = 20
∴ a = 5
∴ Required polynomial = x4 – 2x3 + 3x2 – 5x + 3(5) – 7 .....[Put a = 5 on p(x)]
= x4 – 2x3 + 3x2 – 5x + 15 – 7
= x4 – 2x3 + 3x2 – 5x + 8
When we divide p(x) by x + 2, then we get the remainder p(– 2)
Now, p(– 2) = (– 2)4 – 2(– 2)3 + 3(– 2)2 – 5(– 2) + 8
= 16 + 16 + 12 + 10 + 8
= 62
Hence, the value of a 5 and remainder is 62.
Q3. If both x – 2 and x – 1/2 are factors of px2 + 5x + r, show that p = r.
Solution: As (x - 2)and (x - 1/2)are the factors of the polynomial px2 + 5x + r
i.e., f(2) = 0 and f(1/2) = 0
Now,
f(2) = p(2)2 + 5(2) + r = 0
4p + r = -10 .....(1)
And
p/4 + 5/2 + r = 0
p + 10 + 4x = 0p + 4x = -10 ........(2)
From equation (1) and (2), we get
4p + r = p + 4r
3p = 3x
p = r
Q4. Without actual division, prove that 2x4 – 5x3 + 2x2 – x + 2 is divisible by x2 – 3x + 2.
Solution: Let p(x) = 2x4 – 5x3 + 2x2 – x + 2 firstly, factorise x2 - 3x + 2.
Now, x2 - 3x + 2 = x2 - 2x - x + 2 [by splitting middle term]
= x(x-2)-1 (x-2)
= (x-1)(x-2)
Hence, 0 of x2 - 3x + 2 are land 2.
We have to prove that, 2x4 – 5x3 + 2x2 – x + 2 is divisible by x2 - 3x + 2 i.e., to prove that p (1) =0 and p(2) =0
Now, p(1) = 2(1)4 – 5(1)3 + 2(1)2 -1 + 2
= 2 - 5 + 2 - 1 + 2
= 6 - 6
= 0
and p(2) = 2(2)4 – 5(2)3 + 2(2)2 – 2 + 2
= 2x16 - 5x8 + 2x4 + 0
= 32 – 40 + 8
= 40 – 40
= 0
Hence, p(x) is divisible by x2 - 3x + 2.
Q5. Simplify (2x – 5y)3 – (2x + 5y)3.
Solution: (2x -5y)3 – (2x + 5y)3
= [(2x)3 – (5y)3 – 3(2x)(5y)(2x – 5y)] -[(2x)3 + (5y)3 + 3(2x)(5y)(2x+5y)]
[using identity, (a – b)3 = a3 -b3 – 3ab and (a + b)3 = a3 +b3 + 3ab]
= (2x)3 – (5y)3 – 30xy(2x – 5y) – (2x)3 – (5y)3 – 30xy (2x + 5y)
= -2 (5y)3 – 30xy(2x – 5y + 2x + 5y)
= -2 x 125y3 – 30xy(4x)
= -250y3 -120x2y
Q6. Multiply x2 + 4y2 + z2 + 2xy + xz – 2yz by (– z + x – 2 y).
Solution: (x–2y–z)(x2 + 4y2 + z2 + 2xy + xz − 2yz)
= (x − 2y − z)[(x)2 + (−2y)2 + (−z)2 − (x)(−2y) − (−2y)(−z) − (x)(−z)]
= (x)3 + (−2y)3 +(−z)3 – 3(x)(−2y)(−z)
[Using the identity, a3 + b3 + c3 − 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)]
= x3 – 8y3 – z3 – 6xyz
Q7. If a, b, c are all non-zero and a + b + c = 0, prove that 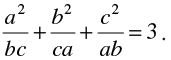
Solution: To prove,
We know that, a3 + b3 + c3 – 3abc = (a + b + c) (a2 + b2 + c2 – ab – bc – ca)
= 0(a2 + b2 + c2 – ab – bc – ca) [∵ a + b + c = 0 , given]
= 0
→ a3 + b3 + c3 = 3 abc
On dividing both sides by abc; we get,
Q8. If a + b + c = 5 and ab + bc + ca = 10, then prove that a3 + b3 + c3 –3abc = – 25.
Solution: Given: a + b + c = 5 and ab + bc + ca = 10
We know that: a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)
= (a + b + c)[a2 + b2 + c2 – (ab + bc + ca)]
= 5{a2 + b2 + c2 – (ab + bc + ca)} = 5(a2 + b2 + c2 – 10)
Given: a + b + c = 5
Now, squaring both sides, get: (a + b + c)2 = 52
a2 + b2 + c2 + 2(ab + bc + ca)
= 25 a2 + b2 + c2 + 2 × 10
= 25 a2 + b2 + c2 = 25 – 20
= 5
Now, a3 + b3 + c3 – 3abc = 5(a2 + b2 + c2 – 10)
= 5 × (5 – 10)
= 5 × (– 5)
= – 25Hence proved.
Q9. Prove that (a + b + c)3 – a3 – b3 – c3 = 3(a + b ) ( b + c) (c + a).
Solution: To prove: (a + b + c)3 – a3 – b3 – c3 = 3(a + b)(b + c)(c + a)
L.H.S = [(a + b + c)3 – a3] – (b3 + c3)
= (a + b + c – a)[(a + b + c)2 + a2 + a(a + b + c)] – [(b + c)(b2 + c2 – bc)] .......[Using identity, a3 + b3 = (a + b)(a2 + b2 – ab) and a3 – b3 = (a – b)(a2 + b2 + ab)]
= (b + c)[a2 + b2 + c2 + 2ab + 2bc + 2ca + a2 + a2 + ab + ac] – (b + c)(b2 + c2 – bc)
= (b + c)[b2 + c2 + 3a2 + 3ab + 3ac – b2 – c2 + 3bc]
= (b + c)[3(a2 + ab + ac + bc)]
= 3(b + c)[a(a + b) + c(a + b)]
= 3(b + c)[(a + c)(a + b)]
= 3(a + b)(b + c)(c + a) = R.H.S
Hence proved.
|
170 videos|914 docs|251 tests
|
FAQs on NCERT Exemplar Solutions: Polynomials - 2 - Mathematics for Grade 9
| 1. What are polynomials in mathematics? |  |
| 2. How do you add or subtract polynomials? |  |
| 3. What is the degree of a polynomial? |  |
| 4. How do you multiply polynomials? |  |
| 5. What are the different types of polynomials? |  |