Class 9 Maths Chapter 6 Question Answers - Triangles
Q1: In the given figure, AD = BC and BD = AC, prove that ∠DAB = ∠CBA
Ans: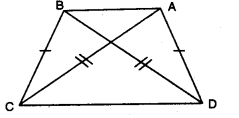 In ∆DAB and ∆CBA, we have
In ∆DAB and ∆CBA, we have
AD = BC [given]
BD = AC [given]
AB = AB [common]
∴ ∆DAB ≅ ∆CBA [by SSS congruence axiom]
Since corresponding parts of congruent triangles are equal [c.p.c.t]
Thus, ∠DAB =∠CBA
Q2: In the given figure, if ∠1 = ∠2 and ∠3 = ∠4, then prove that BC = CD.
Ans: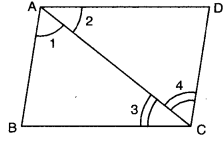 In ∆ABC and ACDA, we have
In ∆ABC and ACDA, we have
∠1 = ∠2 (given)
AC = AC [common]
∠3 = ∠4 [given]
∆ABC ≅ ∆CDA [by ASA congruence axiom]
Since corresponding parts of congruent triangles are equal [c.p.c.t]
∴ BC = CD
Q3: In the given figure, AC > AB and D is a point on AC such that AB = AD. Show that BC > CD.
Ans: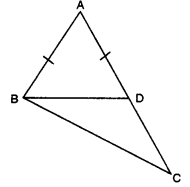 Here, in ∆ABD, AB = AD
Here, in ∆ABD, AB = AD
∠ABD = ∠ADB
[∠s opp. to equal sides of a ∆]
In ∆BAD
ext. ∠BDC = ∠BAD + ∠ABD
⇒ ∠BDC > ∠ABD ….(ii)
Also, in ∆BDC .
ext. ∠ADB > ∠CBD …(iii)
From (ii) and (iii), we have
∠BDC > CD [∵ sides opp. to greater angle is larger]
Q4: In the given figure, ∆ABD and ABCD are isosceles triangles on the same base BD. Prove that ∠ABC = ∠ADC.
Ans: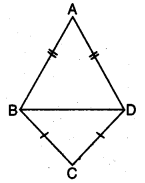 In ∆ABD, we have
In ∆ABD, we have
AB = AD (given)
∠ABD = ∠ADB [angles opposite to equal sides are equal] …(i)
In ∆BCD, we have
CB = CD
⇒ ∠CBD = ∠CDB [angles opposite to equal sides are equal] … (ii)
Adding (i) and (ii), we have
∠ABD + ∠CBD = ∠ADB + ∠CDB
⇒ ∠ABC = ∠ADC
Q5: In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.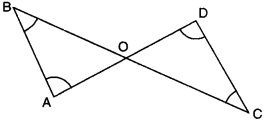 Ans:
Ans:
Here, ∠B < ∠A
⇒ AO < BO …..(i)
and ∠C < ∠D
⇒ OD < CO …..(ii)
[∴ side opposite to greater angle is longer]
Adding (i) and (ii), we obtain
AO + OD < BO + CO
AD < BC
Q6: In a triangle ABC, D is the mid-point of side AC such that BD = 1/2 AC. Show that ∠ABC is a right angle.
Ans: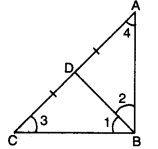 Here, in ∆ABC, D is the mid-point of AC.
Here, in ∆ABC, D is the mid-point of AC.
⇒ AD = CD = 1/2AC …(i)
Also, BD = 1/2AC… (ii) [given]
From (i) and (ii), we obtain
AD = BD and CD = BD
⇒ ∠2 = ∠4 and ∠1 = ∠3 …..(iii)
In ∆ABC, we have
∠ABC + ∠ACB + ∠CAB = 180°
⇒ ∠1 + ∠2 + ∠3 + ∠4 = 180°
⇒ ∠1 + ∠2 + ∠1 + ∠2 = 180° [using (iii)]
⇒ 2(∠1 + ∠2) = 180°
⇒ ∠1 + ∠2 = 90°
Hence, ∠ABC = 90°
Its a right-angled triangle
Q7: ABC is an isosceles triangle with AB = AC. P and Q are points on AB and AC respectively such that AP = AQ. Prove that CP = BQ.
Ans: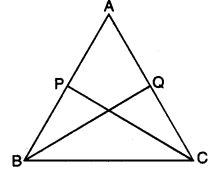 In ∆ABQ and ∆ACP, we have
In ∆ABQ and ∆ACP, we have
AB = AC (given)
∠BAQ = ∠CAP [common]
AQ = AP (given)
∴ By SAS congruence criteria, we have
∆ABQ ≅ ∆ACP
CP = BQ
Q8: In figure, ‘S’ is any point on the side QR of APQR. Prove that PQ + QR + RP > 2PS.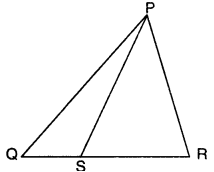 Ans:
Ans:
In ∆PQS, we have
PQ + QS > PS …(i)
[∵ sum of any two sides of a triangle is greater than the third side]
In ∆PRS, we have
RP + RS > PS …(ii)
Adding (i) and (ii), we have
PQ + (QS + RS) + RP > 2PS
Hence, PQ + QR + RP > 2PS. [∵ QS + RS = QR]
Q9: If two isosceles triangles have a common base, prove that the line joining their vertices bisects them at right angles.
Ans: Here, two triangles ABC and BDC having the common base BC,
such that AB = AC and DB = DC.
Now, in ∆ABD and ∆ACD
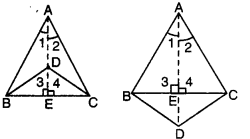
AB = AC [given]
BD = CD [given]
AD = AD [common]
∴ ΔABD ≅ ΔΑCD [by SSS congruence axiom]
⇒ ∠1 = ∠2 [c.p.c.t.]
Again, in ∆ABE and ∆ACE, we have
AB = AC [given]
∠1 = ∠2 [proved above]
AE = AE [common]
∆ABE = ∆ACE [by SAS congruence axiom]
BE = CE [c.p.c.t.]
and ∠3 = ∠4 [c.p.c.t.]
But ∠3 + ∠4 = 180° [a linear pair]
⇒ ∠3 = ∠4 = 90°
Hence, AD bisects BC at right angles.
Q10: In the given figure, in ∆ABC, ∠B = 30°, ∠C = 65° and the bisector of ∠A meets BC in X. Arrange AX, BX and CX in ascending order of magnitude.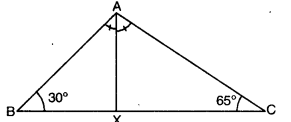 Ans:
Ans:
Here, AX bisects ∠BAC.
∴ ∠BAX = ∠CAX = x (say)
Now, ∠A + ∠B + C = 180° [angle sum property of a triangle]
⇒ 2x + 30° + 65° = 180°
⇒ 2x + 95 = 180°
⇒ 2x = 180° – 95°
⇒ 2x = 85°
⇒ x = 85∘ / 2 = 42.59
In ∆ABX, we have x > 30°
BAX > ∠ABX
⇒ BX > AX (side opp. to larger angle is greater)
⇒ AX < BX
Also, in ∆ACX, we have 65° > x
⇒ ∠ACX > ∠CAX
⇒ AX > CX [side opp. to larger angle is greater]
⇒ CX > AX … (ii)
Hence, from (i) and (ii), we have
CX < AX < BX
Q11: In the given figure, ∆ABC and ∆DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC, AD is extended to intersect BC at P. Show that : (i) ∆ABD ≅ ∆ACD (ii) ∆ABP ≅ ∆ACP Ans:
Ans:
(i) In ∆ABD and ∆ACD
AB = AC [given]
BD = CD [given]
AD = AD [common)]
∴ By SSS congruence axiom, we have
∆ABD ≅ ∆ACD
(ii) In ∆ABP and ∆ACP
AB = AC [given]
∠BAP = ∠CAP [c.p.cit. as ∆ABD ≅ ∆ACD]
AP = AP [common]
∴ By SAS congruence axiom, we have
∆ABP ≅ ∆ACP
Q12: In the given figure, it is given that AE = AD and BD = CE. Prove that ∆AEB ≅ ∆ADC.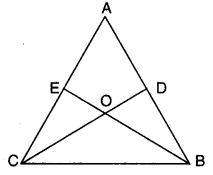 Ans:
Ans:
We have AE = AD … (i)
and CE = BD … (ii)
On adding (i) and (ii),
we have AE + CE = AD + BD
⇒ AC = AB
Now, in ∆AEB and ∆ADC,
we have AE = AD [given]
AB = AC [proved above]
∠A = ∠A [common]
∴ By SAS congruence axiom, we have
∆AEB = ∆ADC
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths Chapter 6 Question Answers - Triangles
| 1. What is the sum of the interior angles of a triangle? |  |
| 2. How do you classify triangles based on their sides? |  |
| 3. What are the different types of triangles based on their angles? |  |
| 4. How can you calculate the area of a triangle? |  |
| 5. What is the Pythagorean theorem and how does it relate to triangles? |  |






















