The Mid Point Theorem | Mathematics (Maths) Class 9 PDF Download

Mid Point Theorem
Geometry is an important part of mathematics that deals with different shapes and figures. Triangles are an important part of geometry and the mid-point theorem points towards mid points of the triangle.What is Mid-Point Theorem?
This theorem states that” The line segment joining mid-points of two sides of a triangle is parallel to the third side of the triangle and is half of it”
Proof of Mid-Point Theorem
A triangle ABC in which D is the mid-point of AB and E is the mid-point of AC.
To Prove: DE ∥ BC and DE = 1/2(BC)
Construction
Extend the line segment joining points D and E to F such that DE = EF and join CF.
Proof
In ∆AED and ∆CEF
DE = EF (construction)
∠1 = ∠2 (vertically opposite angles)
AE = CE (E is the mid-point)
△AED ≅ △CEF by SAS criteria
Therefore,
∠3 =∠4 (c.p.c.t)
But these are alternate interior angles.
So, AB ∥ CF
AD = CF(c.p.c.t)
But AD = DB (D is the mid-point)
Therefore, BD = CF
In BCFD
BD∥ CF (as AB ∥ CF)
BD = CF
BCFD is a parallelogram as one pair of opposite sides is parallel and equal.
Therefore,
DF∥ BC (opposite sides of parallelogram)
DF = BC (opposite sides of parallelogram)
As DF∥ BC, DE∥ BC and DF = BC
But DE = EF
So, DF = 2(DE)
2(DE) = BC
DE = 1/2(BC)
Hence, proved that the line joining mid-points of two sides of the triangle is parallel to the third side and is half of it.
What is the Converse of Mid-Point Theorem?
The line drawn through the mid-point of one side of a triangle parallel to the base of a triangle bisects the third side of the triangle.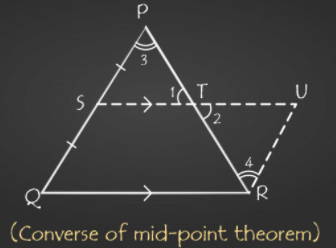
Proof of the Theorem
In triangle PQR, S is the mid-point of PQ and ST ∥ QR
To Prove: T is the mid-point of PR.
Construction
Draw a line through R parallel to PQ and extend ST to U.
Proof
ST∥ QR(given)
So, SU∥ QR
PQ∥ RU (construction)
Therefore, SURQ is a parallelogram.
SQ = RU(Opposite sides of parallelogram)
But SQ = PS (S is the mid-point of PQ)
Therefore, RU = PS
In △PST and △RUT
∠1 =∠2(vertically opposite angles)
∠3 =∠4(alternate angles)
PS = RU(proved above)
△PST ≅ △RUT by AAS criteria
Therefore, PT = RT
T is the mid-point of PR.
Sample Problems on Mid Point Theorem
Problem 1: l, m, and n are three parallel lines. p and q are two transversals intersecting parallel lines at A, B, C, D, E, and F as shown in the figure. If AB:BC = 1:1, find the ratio of DE : EF.
Given: AB:BC=1:1
To find: DE:EF
Construction: Join AF such that it intersects line m at G.
In △ACF
AB = BC(1:1 ratio)
BG∥ CF(as m∥n)
Therefore, by converse of mid-point theorem G is the midpoint of AF(AG = GF)
Now, in △AFD
AG = GF(proved above)
GE∥ AD(as l∥m)
Therefore, by converse of mid-point theorem E is the mid-point of DF(FE = DE)
So, DE:EF = 1:1(as they are equal)
Problem 2: In the figure given below L, M and N are mid-points of side PQ, QR, and PR respectively of triangle PQR.
If PQ = 8cm, QR = 9cm and PR = 6cm. Find the perimeter of the triangle formed by joining L, M, and N.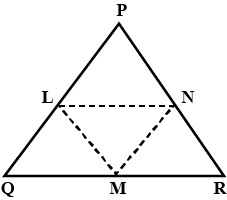
Solution: As L and N are mid-points
By mid-point theorem
LN ∥ QR and LN = 1/2 * (QR)
LN = 1/2 × 9 = 4.5cm
Similarly, LM = 1/2 * (PR) = 1/2×(6) = 3cm
Similarly, MN = 1/2 * (PQ) = 1/2 × (8) = 4cm
Therefore, the perimeter of △LMN is LM + MN + LN
= 3 + 4 + 4.5
= 11.5cm
Perimeter is 11.5 cm
Result: Perimeter of the triangle formed by joining mid-points of the side of the triangle is half of the triangle.
|
44 videos|412 docs|54 tests
|
FAQs on The Mid Point Theorem - Mathematics (Maths) Class 9
| 1. What is the Mid Point Theorem in geometry? |  |
| 2. How can I apply the Mid Point Theorem in solving triangle problems? |  |
| 3. Can the Mid Point Theorem be used in non-triangle geometric shapes? |  |
| 4. What are the implications of the Mid Point Theorem in coordinate geometry? |  |
| 5. Are there any real-world applications of the Mid Point Theorem? |  |

|
Explore Courses for Class 9 exam
|

|


















