NCERT Solutions for Class 8 Maths - Algebraic Expressions and Identities - 1 (Exercise 8.1 and 8.2)

Exercise 8.1
Q1. Add the following:
(i) ab – bc, bc – ca, ca – ab
Ans: (ab – bc) + (bc – ca) + (ca-ab)
= ab – bc + bc – ca + ca – ab
= ab – ab – bc + bc – ca + ca
= 0
(ii) (a – b + ab) + (b – c + bc) + (c – a + ac)
= a – b + ab + b – c + bc + c – a + ac
= a – a +b – b +c – c + ab + bc + ca
= 0 + 0 + 0 + ab + bc + ca
= ab + bc + ca
iii) 2p2q2 – 3pq + 4, 5 + 7pq – 3p2q2
= (2p2q2 – 3pq + 4) + (5 + 7pq – 3p2q2)
= 2p2q2 – 3p2q2 – 3pq + 7pq + 4 + 5
= – p2q2 + 4pq + 9
(iv) l2 + m2, m2 + n2, n2 + l2, 2lm + 2mn + 2nl
Ans: (l2 + m2) + (m2 + n2) + (n2 + l2) + (2lm + 2mn + 2nl)
= l2 + l2 + m2 + m2 + n2 + n2 + 2lm + 2mn + 2nl
= 2l2 + 2m2 + 2n2 + 2lm + 2mn + 2nl
Q2. (a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3
Ans: (12a – 9ab + 5b – 3) – (4a – 7ab + 3b + 12)
= 12a – 9ab + 5b – 3 – 4a + 7ab – 3b – 12
= 12a – 4a -9ab + 7ab +5b – 3b -3 -12
= 8a – 2ab + 2b – 15
(b) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
Ans: (5xy – 2yz – 2zx + 10xyz) – (3xy + 5yz – 7zx)
= 5xy – 2yz – 2zx + 10xyz – 3xy – 5yz + 7zx
=5xy – 3xy – 2yz – 5yz – 2zx + 7zx + 10xyz
= 2xy – 7yz + 5zx + 10xyz
(c) Subtract 4p2q – 3pq + 5pq2 – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq2 + 5p2q
Ans: (18 – 3p – 11q + 5pq – 2pq2 + 5p2q) – (4p2q – 3pq + 5pq2 – 8p + 7q – 10)
= 18 – 3p – 11q + 5pq – 2pq2 + 5p2q – 4p2q + 3pq – 5pq2 + 8p – 7q + 10
=18+10 -3p+8p -11q – 7q + 5 pq+ 3pq- 2pq2 – 5pq^2 + 5 p^2 q – 4p^2 q
= 28 + 5p – 18q + 8pq – 7pq2 + p2q
Exercise 8.2
Q1: Find the product of the following pairs of monomials.
(i) 4, 7p
Ans: 4 , 7 p = 4 × 7 × p = 28p
(ii) –4p, 7p
Ans: – 4p × 7p = (-4 × 7 ) × (p × p )= -28p2
(iii) –4p, 7pq
Ans: – 4p × 7pq =(-4 × 7 ) (p × pq) = -28p2q
(iv) 4p3, –3p
Ans: 4p3 × – 3p = (4 × -3 ) (p3 × p ) = -12p4
(v) 4p, 0
Ans: 4p × 0 = 4 × p × 0 =0
Q2: Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively.
(p, q); (10m, 5n); (20x2, 5y2); (4x, 3x2); (3mn, 4np)
Ans: We know that,
Area of rectangle = length × breadth
Area of 1st rectangle = p × q = pq
Area of 2nd rectangle = 10m × 5n = 10 × 5 × m × n = 50mn
Area of 3rd rectangle = 20x2 × 5y2 = 20 × 5 × x2 × y2 = 100x2y2
Area of 4th rectangle = 4x × 3x2 = 4 × 3 × x × x2 = 12x3
Area of 5th rectangle = 3mn × 4np = 3 × 4 × m × n × n × p = 12mn2p
Q3: Complete the table of products.
Ans: The table can be completed as follows.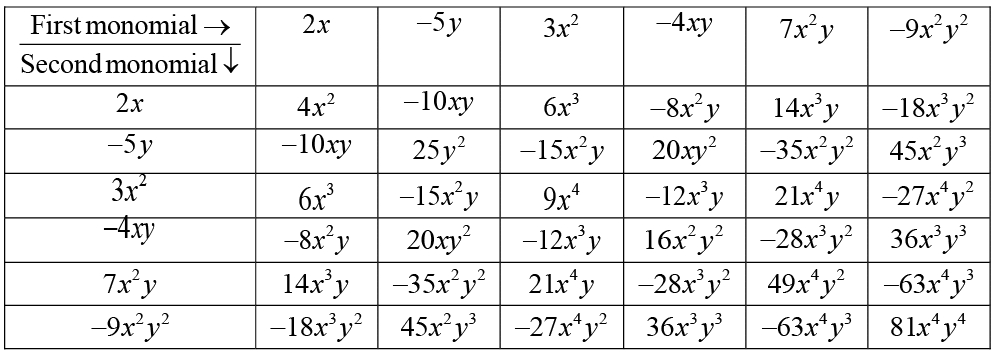
Q4. Obtain the volume of rectangular boxes with the following length, breadth and height respectively.
(i) 5a, 3a2, 7a4
Ans: We know that
Volume = length × breadth × height
Volume = 5a × 3a2 × 7a4 = 105a7
(ii) 2p, 4q, 8r
Ans: We know that
Volume = length × breadth × height
Volume = 2p × 4q × 8r = 64pqr
(iii) xy, 2x2y, 2xy2
Ans: We know that
Volume = length x breadth x height
Volume = xy × 2x2y × 2xy2 = 4x4y4
(iv) a, 2b, 3c
Ans: We know that
Volume = length × breadth × height
Volume = a × 2b × 3c = 6abc
Q5. Obtain the product of
(i) xy, yz, zx
Ans: xy × yz × zx = x2 y2 z2
(ii) a, – a2, a3
Ans: a × – a2 × a3 = – a6
(iii) 2, 4y, 8y2, 16y3
Ans: 2 × 4y × 8y2 × 16y3 = 1024 y6
(iv) a, 2b, 3c, 6abc
Ans: a × 2b × 3c × 6abc = 36a2 b2 c2
(v) m, – mn, mnp
Ans: m × – mn × mnp = –m3 n2 p
|
94 videos|549 docs|42 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Algebraic Expressions and Identities - 1 (Exercise 8.1 and 8.2)
| 1. What are algebraic expressions and how are they formed? |  |
| 2. What are the different types of algebraic expressions? |  |
| 3. How do you simplify algebraic expressions? |  |
| 4. What is the significance of identities in algebra? |  |
| 5. How can I apply algebraic identities to solve problems? |  |






















