Q.1. Find the term independent of x, x ≠ 0, in the expansion of .
.
Ans.
General Term Tr+1 = nCrxn–ryr

For getting the term independent of x,
30 – 3r = 0 ⇒ r = 10
On putting the value of r in the above expression, we get

Hence, the required term = 
Q.2. If the term free from x in the expansion of is 405, find the value of k.
is 405, find the value of k.
Ans.
The given expression is
General term Tr+1 = nCr xn-r yr


For getting term free from x, 
⇒ r = 2
On putting the value of r in the above expression, we get
10C2 (–K)2
According to the condition of the question, we have

⇒ 45K2 = 405 ⇒ 
∴ K = ± 3
Hence, the value of K = ±3
Q.3. Find the coefficient of x in the expansion of (1 – 3x + 7x2) (1 – x)16.
Ans.
The given expression is (1 – 3x + 7x2) (1 – x)16 = (1 – 3x + 7x2) [16C0(1)16(–x)0 + 16C1(1)15 (–x) + 16C2(1)14 (–x)2 + …]
= (1 – 3x + 7x2) (1 – 16x + 120x2 …)
Collecting the term containing x, we get –16x – 3x = – 19x
Hence, the coefficient of x = –19
Q.4. Find the term independent of x in the expansion of, 
Ans.
Given expression is
General term Tr+1 = nCrxn–ryr

For getting a term independent of x, put 15 – 3r = 0 ⇒ r = 5
∴ The required term is 15C5(3)15-5(-2)5

Hence, the required term = –3003 (3)10 (2)5
Q.5. Find the middle term (terms) in the expansion of
(i)
(ii)
Ans.
(i) Given expression is
Number of terms = 10 + 1 = 11 (odd)
∴ Middle term =
General Term Tr+1 = nCrxn–r yr

Hence, the required middle term = – 252
(ii) Given expression is
Number of terms = 9 + 1 = 10 (even)
∴ Middle terms are
 = 5th term and (5 + 1) = 6th term
= 5th term and (5 + 1) = 6th term
General Term Tr+1 = nCrxn–ryr


Now, T6 = T5+1 =



Hence, the required middle terms are 
Q.6. Find the coefficient of x15 in the expansion of (x – x2)10.
Ans.
The given expression is (x – x2)10
General Term Tr+1 = nCrxn–ryr
= 10Cr(x)10–r (–x2)r = 10Cr(x)10–r (–1)r × (x2)r
= (-1)r × 10Cr(x)10-r+2r = (- 1)r × 10Cr(x)10+r
To find the coefficient of x15, Put 10 + r = 15 ⇒ r = 5
∴ Coefficient of x15 = (-1)5 10C5 = - 10C5 = - 252
Hence, the required coefficient = - 252
Q.7. Find the coefficient of in the expansion of
in the expansion of
Ans.
The given expression is
General Term Tr+1 = nCrxn–ryr = 15Cr(4)15-r
= 15Cr (x)60 – 4r (- 1)r


To find the coefficient of Put 7r – 60 = 17
Put 7r – 60 = 17
⇒ 7r = 60 + 17 ⇒ 7r = 77
∴ r = 11
Putting the value of r in the above expression, we get

Hence, the coefficient of
Q.8. Find the sixth term of the expansion f the binomial coefficient of the third term from the end is 45.
f the binomial coefficient of the third term from the end is 45.
[Hint: Binomial coefficient of third term from the end = Binomial coefficient of third term from beginning = nC2.]
Ans.
The given expression is ( y1/2 + x1/3 )n, since the binomial
coefficient of third term from the end =
Binomial coefficient of third term from the beginning = nC2
∴ nC2 = 45
⇒  ⇒ n2 – n = 90
⇒ n2 – n = 90
⇒ n2 – n – 90 = 0 ⇒ n2 – 10n + 9n – 90 = 0
⇒ n(n – 10) + 9(n – 10) ⇒ (n – 10) (n + 9) = 0
⇒ n = 10, n = - 9 ⇒ n = 10, n ≠ - 9
So, the given expression becomes (y1/2 + x1/3)10
Sixth term is this expression
T6 = T5+1 = 10C5(y1/2)10–5 (x1/3)5 = 10C5y5/2 × x5/3
= 252 y5/2x5/3
Hence, the required term = 252 y5/2 . x5/3
Q.9. Find the value of r, if the coefficients of (2r + 4)th and (r – 2)th terms in the expansion of (1 + x)18 are equal.
Ans.
General Term Tr+1 = nCr xn–ryr
For coefficient of (2r + 4)th term, we have
T2r+4 = T2r+3+1 = 18C2r+3 (1)18–2r–3 × x2r+3
∴ Coefficient of (2r + 4)th term = 18C2r+3
Similarly, Tr-2 = Tr-3+1 = 18Cr-3 (1)18-r+3 × xr-3
∴ Coefficient of (r - 2)th term = 18Cr3
As per the condition of the questions, we have 18C2r+3 = 18Cr-3
⇒ 2r + 3 + r - 3 = 18 ⇒ 3r = 18 ⇒ r = 6
Q.10. If the coefficient of second, third and fourth terms in the expansion of (1 + x)2n are in A.P. Show that 2n2 – 9n + 7 = 0.
Ans.
Given expression = (1 + x )2n
Coefficient of second term = 2nC1
Coefficient of third term = 2nC2
and coefficient of fourth term = 2nC3
As the given condition, 2nC1, 2nC2 and 2nC3 are in A.P.
∴ 2nC2 – 2nC1 = 2nC3 – 2nC2
⇒ 2 × 2nC2 = 2nC1 + 2nC3


⇒ 
⇒ 
⇒ 12n – 6 = 6 + 4n2 – 4n – 2n + 2
⇒ 4n2 – 6n – 12n + 2 + 12 = 0
⇒ 4n2 – 18n + 14 = 0
⇒ 2n2 – 9n + 7 = 0
Hence proved.
Q.11. Find the coefficient of x4 in the expansion of (1 + x + x2 + x3)11.
Ans.
Given expression is (1 + x + x2 + x3)11
= [(1 + x) + x2 (1 + x)]11 = [(1 + x) (1 + x2)]11
= (1 + x)11 × (1 + x2)11
Expanding the above expression, we get (11C0 + 11C1x + 11C2x2 + 11C3x3 + 11C4x4 + …) × (11C0 + 11C1x2 + 11C2x4 + )
=(1 + 11x + 55x2 + 165x3 + 330x4 …) × (1 + 11x2 + 55x4 + &)
Collecting the terms containing x4, we get
(55 + 605 + 330)x4 = 990x4
Hence, the coefficient of x4 = 990
Long AnswerType
Q.12. If p is a real number and if the middle term in the expansion of  is 1120, find p.
is 1120, find p.
Ans.
Given expression is
Number of terms = 8 + 1 = 9 (odd)
∴ Middle term =  term = 5th term
term = 5th term
∴ 

Now 8C4P4 = 1120 ⇒ 
⇒ 70P4 = 1120
⇒ 
Hence, the required value of P = ±2
Q.13. Show that the middle term in the expansion of is
is

Ans.
Given expression is
Number of terms = 2n + 1 (odd)
∴ Middle term =  th i.e., (n + 1)th term
th i.e., (n + 1)th term



Hence, the middle term =
Q.14. Find n in the binomial  if the ratio of 7th term from the beginning to the 7th term from the end is
if the ratio of 7th term from the beginning to the 7th term from the end is
Ans.
The given expression is

General Term Tr+1 = nCrxn–ryr

7th term from the end = (n – 7 + 2)th term from the beginning = (n – 5)th term from the beginning
So,

According to the question, we get



Hence, the required value of n is 9.
Q.15. In the expansion of (x + a)n if the sum of odd terms is denoted by O and the sum of even term by E. Then prove that
(i) O2 – E2 = (x2 – a2)n
(ii) 4OE = (x + a)2n – (x – a)2n
Ans.
Given expression is (x + a)n
(x + a)n = nC0xna0 + nC1xn–1a + nC2xn–2a2 + nC3xn–3a3 + … + nCnan
Sum of odd terms,
O = nC0 xn + nC2 xn- 2 a2+ nC4 xn- 4 a4+ ...
and the sum of even terms
E = nC1 xn-1 × a + nC3 xn- 3a3+ nC5 xn- 5a5+ ...
Now (x + a)n = O + E ...(i)
Similarly (x - a)n = O - E ...(ii)
Multiplying eq. (i) and eq. (ii), we get,
(x + a)n (x – a)n = (O + E) (O – E)
⇒ (x2 – a2)n = O2 – E2
Hence O2 – E2 = (x2 – a2)n
(ii) 4OE = (O + E)2 – (O – E)2
= [(x + a)n]2 – [(x – a)n]2
= [x + a]2n – [x – a]2n
Hence, 4OE = (x + a)2n – (x – a)2n
Q.16. If xp occurs in the expansion of prove that its coefficient is
prove that its coefficient is 
Ans.
Given expression is 
General terms, Tr+1 = nCrxn–ryr

If xp occurs in
then 4n – 3r = p ⇒ 3r = 4n - p
⇒
∴ Coefficient of xp =

Hence, the coefficient of xp =
Q.17. Find the term independent of x in the expansion of (1 + x + 2x3)
Ans.
Given expression is
Let us consider
General Term Tr+1 = nCrxn–ryr


So, the general term in the expansion of

For getting the term independent of x,
Put 18 – 3r = 0, 19 – 3r = 0 and 21 – 3r = 0, we get

The possible value of r are 6 and 7
∴ The term independent of x is

Hence, the required term = 
Objective Type Questions
Q.18. The total number of terms in the expansion of (x + a)100 + (x – a)100 after simplification is
(a) 50
(b) 202
(c) 51
(d) none of these
Ans. (c)
Solution.
Number of terms in the expansion of (x + a)100 = 101
Number of terms in the expansion of (x – a)100 = 101
Now 50 terms of expansion will cancel out with negative 50 terms of (x – a)100 So, the remaining 51 terms of first expansion will be added to 51 terms of other.
Therefore, the number of terms = 51
Hence, the correct option is (c).
Q.19. Given the integers r > 1, n > 2, and coefficients of (3r)th and (r + 2)nd terms in the binomial expansion of (1 + x)2n are equal, then
(a) n = 2r
(b) n = 3r
(c) n = 2r + 1
(d) none of these
Ans. (a)
Solution.
Given that r > 1 and n > 2
then T3r = T3r–1+1 = 2nC3r–1 × x3r–1
and Tr+2 = Tr +1+1 = 2nCr +1 xr +1
As per the question, we have
As per the question, we have
2nC3r–1 = 2nCr+1
⇒ 3r – 1 + r + 1 = 2n [∴ nCp = nCq ⇒ n = p + q]
⇒ 4r = 2n
n = 2r
Hence, the correct option is (a).
Q.20. The two successive terms in the expansion of (1 + x)24 whose coefficients are in the ratio 1:4 are
(a) 3rd and 4th
(b) 4th and 5th
(c) 5th and 6th
(d) 6th and 7th
[Hint:  ⇒ 4r + 4 = 24 – 4 ⇒ r = 4 ]
⇒ 4r + 4 = 24 – 4 ⇒ r = 4 ]
Ans. (c)
Solution.
Let rth and (r + 1)th be two successive terms in the expansion (1 + x)24
∴ Tr+1 = 24Cr × xr
Tr+2 = Tr+1+1 = 24Cr+1xr+1
As per the question, we have


⇒ 5r = 20 ⇒ r = 4
∴ T4+1 = T5 and T4+2 = T6
Hence, the correct option is (c).
Q.21. The coefficient of xn in the expansion of (1 + x)2n and (1 + x)2n – 1 are in the ratio.
(a) 1 : 2
(b) 1 : 3
(c) 3 : 1
(d) 2 : 1
[Hint : 2nCn : 2n – 1Cn
Ans. (d)
Solution.
General Term Tr+1 = nCr xn–r yr
In the expansion of (1 + x)2n, we get Tr+1 = 2nCr xr
To get the coefficient of xn, put r = n
∴ Coefficient of xn = 2nCn
In the expansion of (1 + x)2n-1, we get Tr+1 = 2n-1Crxr
∴ Coefficient of xn is 2n-1Cn-1
The required ratio is


Hence, the correct option is (d).
Q.22. If the coefficients of 2nd, 3rd and the 4th terms in the expansion of (1 + x)n are in A.P., then value of n is
(a) 2
(b) 7
(c) 11
(d) 14
[Hint: 2nC2 = nC1 + nC3 ⇒ n2 – 9n + 14 = 0 ⇒ n = 2 or 7]
Ans. (b)
Solution.
Given expression is (1 + x)n
(1 + x)n = nC0 + nC1x + nC2x2 + nC3x3 + … nCnxn Here, coefficient of 2nd term = nC1
Coefficient of 3rd term = nC2
and coefficient of 4th term = nC3
Given that nC1, nC2 and nC3 are in A.P.
∴ 2 . nC2 = nC1 + nC3

⇒ 6n – 6 = 6 + n2 – 3n + 2
⇒ n2 – 3n – 6n + 14 = 0 ⇒ n2 – 9n + 14 = 0
⇒ n2 – 7n – 2n + 14 = 0 ⇒ n(n – 7) – 2(n – 7) = 0
⇒ (n – 2) (n – 7) = 0 ⇒ n = 2, 7 ⇒ n = 7
whereas n = 2 is not possible
Hence, the correct option is (b).
Q.23. If A and B are coefficient of xn in the expansions of (1 + x)2n and (1 + x)2n – 1 respectively, then equals
equals
(a) 1
(b) 2
(c) 1/2
(d) 1/n

Ans. (b)
Solution.
Given expression is (1 + x)2n
Tr+1 = 2nCrxr
∴ Coefficient of xn = 2nCn = A (Given)
In the expression (1 + x)2n–1
Tr+1 = 2n–1Crxr
∴ Coefficient of xn = 2n-1Cn = B (Given)
So  [from Q. no. 21]
[from Q. no. 21]
Hence, the correct option is (b).
Q.24. If the middle term of is equal to
is equal to then value of x is
then value of x is
(a)
(b)
(c) 
(d)

Ans. (c)
Solution.
Given expression is 
Number of terms = 10 + 1 = 11 odd
∴ Middle term = term = 6th term
term = 6th term

⇒ 
⇒ 
∴ 
Hence, the correct option is (c).
Fill in the blanks
Q.25. The largest coefficient in the expansion of (1 + x)30 is _____.
Ans.
Here n = 30 which is even
∴ the largest coefficient in (1 + x)n = nCn/2
So, the largest coefficient in (1 + x)30 = 30C15
Hence, the value of the filler is 30C15.
Q.26. The number of terms in the expansion of (x + y + z)n ________.
[Hint: (x + y + z)n = [x + (y + z)]n]
Ans.
The expression (x + y + z)n can be written a [x + (y + z)]n
∴ [x + (y + z)]n = nC0xn (y + z)0 + nC1(x)n–1 (y + z)
+ nC2(x)n–2 (y + z)2 + … + nCn(y + z)n
∴ Number of terms 1 + 2 + 3 + 4 + & (n + 1)

Hence, the value of the filler is 
Q.27. In the expansion of  the value of constant term is_______.
the value of constant term is_______.
Ans.
Let Tr+1 be the constant term in the expansion of 

For getting constant term, 32 – 4r = 0
⇒ = r = 8
∴ Tr + 1 = (– 1)8 . 16C8 = 16C8
Hence, the value of the filler is 16C8.
Q.28. If the seventh terms from the beginning and the end in the expansion of
 are equal, then n equals _____.
are equal, then n equals _____.


Ans.
The given expansion is
Now the T7 from the end = T7 from the beginning in

As per the questions, we get


Hence, the value of the filler is 12.
Q.29. The coefficient of a– 6 b4 in the expansion of  is _________.
is _________.

Ans.
The given expansion is from a–6b4, we can take r = 4
from a–6b4, we can take r = 4


Hence, the value of the filler = .
.
Q.30. Middle term in the expansion of (a3 + ba)28 is _________ .
Ans.
Number of term in the expansion (a3 + ba)28 = 28 + 1 = 29 (odd)
∴ Middle term =
∴ T15 = T14+1 = 28C14 (a3)28–14 × (ba)14 = 28C14 (a)42 × b14 × a14
= 28C14a56b14
Hence, the value of the filler is 28C14 a56 b14.
Q.31. The ratio of the coefficients of xp and xq in the expansion of (1 + x)p + q is_________ [Hint: p + qCp = p + qCq]
Ans.
Given expansion is (1 + x)p+q
Tr+1 = p + qCr xr
Put r = p = p + qCpxp
∴ the coefficient of xp = p + qCp
Similarly, coefficient of xq = p + qCq

and 
So, the ratio is 1 : 1.
Q.32. The position of the term independent of x in the expansion of
 is _______.
is _______.
Ans.
The given expansion is 


For independent of x, we get

10 – 5r = 0
r = 2
So, the position of the term independent of x is 3rd term.
Hence, the value of the filler is Third term
Q.33. If 2515 is divided by 13, the reminder is _________ .
Ans.
Let 2515 = (26– 1)15
= 15C0 (26)15 (- 1)0 + 15C1 (26)14(- 1)1 + 15C2 (26)13 (- 1)2 + … + 15C15(- 1)15
= 2615 - 15(26)14 + L - 1 - 13 + 13
= 2615 – 15 × (26)14 + … – 13 + 12
= 13λ + 12
∴ The remainder = 12
Hence, the value of the filler is 12.
True or False.
Q.34. The sum of the series 
Ans.
 = 20C0 + 20C1 + 20C2 + 20C3 + … + 20C10
= 20C0 + 20C1 + 20C2 + 20C3 + … + 20C10
= 20C0 + 20C1 + … + 20C10 + 20C11 + … + 20C20 – (20C11+ … + 20C20)
= 220 – (20C11 + … + 20C20)
Hence, the given statement is False.
Q.35. The expression 79 + 97 is divisible by 64.
Hint: 79 + 97 = (1 + 8)7 – (1 – 8)9
Ans.
79 + 97 = (1 + 8)7 – (1 – 8)9 = [7C0 + 7C1 × 8 + 7C2(8)2 + 7C3(8)3 + & + 7C7(8)7] – [9C0 – 9C18 + 9C2(8)2 – 9C3(8)3 + … 9C9(8)9]
= (7 x 8 + 9 x 8) + (21 x 82 - 36 x 82) + &
= (56 + 72) + (21 – 36)82 + … = 128 + 64 (21 – 36) + …
= 64[2 + (21 – 36) + …]
Which is divisible by 64
Hence, the given statement is True.
Q.36. The number of terms in the expansion of [(2x + y3)4]7 is 8
Ans.
Given expression is [(2x + 3y)4]7 = (2x + 3y)28
So, the number of terms = 28 + 1 = 29
Hence, the given statement is False.
Q.37. The sum of coefficients of the two middle terms in the expansion of (1 + x)2n – 1 is equal to 2n – 1Cn.
Ans.
The given expression is (1 + x)2n – 1
Number of terms = 2n – 1 + 1 = 2n (even)
∴ Middle terms are term and
term and terms
terms
= nth terms and (n + 1)th terms
Coefficient of nth term = 2n – 1Cn–1
and the coefficient of (n + 1)th term = 2n – 1Cn
Sum of the coefficients = 2n – 1Cn – 1 + 2n – 1Cn
= 2n – 1Cn–1 + 2n – 1Cn = 2n – 1 + 1Cn = 2nCn
Hence, the statement [∴ nCr + nCr -1 = n+1Cr ] is False.
Q.38. The last two digits of the numbers 3400 are 01.
Ans.
Given that 3400 = (9)200 = (10 – 1)200
∴ (10 – 1)200 = 200C0(10)200 – 200C1(10)199 + … – 200C199(10)1 + 200C200(1)200
= 10200 – 200 x 10199 + & - 10 x 200 + 1
So, it is clear that last two digits are 01.
Hence, the given statement is True.
Q.39. If the expansion of contains a term independent of x, then n is a multiple of 2.
contains a term independent of x, then n is a multiple of 2.
Ans.
The given expression is

For the term independent of x, 2n – 3r = 0
 which not an integer and the expression is not possible to be true Hence, the given statement is False.
which not an integer and the expression is not possible to be true Hence, the given statement is False.
Q.40. Number of terms in the expansion of (a + b)n where n ∈ N is one less
than the power n.
Ans.
Since, the number of terms in the given expression (a + b)n is 1 more than n i.e., n + 1 Hence, the given statement is False.
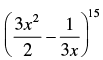 .
.


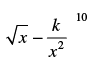 is 405, find the value of k.
is 405, find the value of k.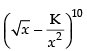



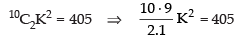






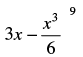





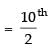 = 5th term and (5 + 1) = 6th term
= 5th term and (5 + 1) = 6th term






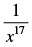 in the expansion of
in the expansion of





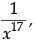 Put 7r – 60 = 17
Put 7r – 60 = 17

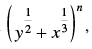 f the binomial coefficient of the third term from the end is 45.
f the binomial coefficient of the third term from the end is 45.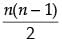 ⇒ n2 – n = 90
⇒ n2 – n = 90



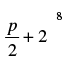 is 1120, find p.
is 1120, find p.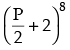
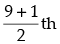 term = 5th term
term = 5th term 



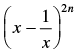 is
is

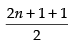 th i.e., (n + 1)th term
th i.e., (n + 1)th term



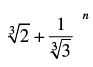 if the ratio of 7th term from the beginning to the 7th term from the end is
if the ratio of 7th term from the beginning to the 7th term from the end is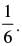
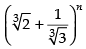
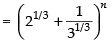






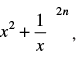 prove that its coefficient is
prove that its coefficient is 







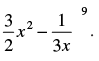
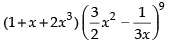








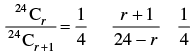 ⇒ 4r + 4 = 24 – 4 ⇒ r = 4 ]
⇒ 4r + 4 = 24 – 4 ⇒ r = 4 ]






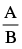 equals
equals
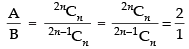 [from Q. no. 21]
[from Q. no. 21]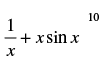 is equal to
is equal to then value of x is
then value of x is





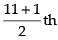 term = 6th term
term = 6th term




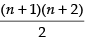
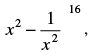 the value of constant term is_______.
the value of constant term is_______.

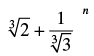 are equal, then n equals _____.
are equal, then n equals _____.





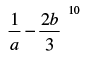 is _________.
is _________.
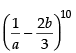 from a–6b4, we can take r = 4
from a–6b4, we can take r = 4

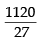 .
.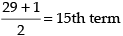


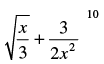 is _______.
is _______.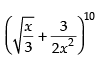
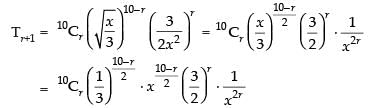

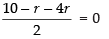

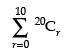 = 20C0 + 20C1 + 20C2 + 20C3 + … + 20C10
= 20C0 + 20C1 + 20C2 + 20C3 + … + 20C10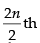 term and
term and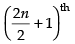 terms
terms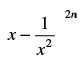 contains a term independent of x, then n is a multiple of 2.
contains a term independent of x, then n is a multiple of 2.

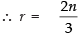 which not an integer and the expression is not possible to be true Hence, the given statement is False.
which not an integer and the expression is not possible to be true Hence, the given statement is False. 























