Worksheet Solution: Ratio and Proportion | Mathematics for Class 5 PDF Download
Q1: Express each of the following ratios in the simplest form.
(a) 5.6 m to 28 cm
Ans: 20 : 1
To express this ratio in simplest form, first, convert 5.6 meters to centimeters.
1 meter = 100 centimeters
So, 5.6 meters = 5.6 × 100 = 560 centimeters.
Now, the ratio becomes 560 cm to 28 cm.
To simplify, divide both sides by the greatest common divisor, which is 28.
560 ÷ 28 = 20
28 ÷ 28 = 1
So, the simplified ratio is 20:1.
(b) dozen to a score
Ans: 3 : 5
A dozen is 12 and a score is 20.
So, the ratio is 12 to 20.
To simplify, divide both sides by the greatest common divisor, which is 4.
12 ÷ 4 = 3
20 ÷ 4 = 5
So, the simplified ratio is 3:5.
(c) score to a gross
Ans: 5 : 36
A score is 20 and a gross is 144.
So, the ratio is 20 to 144.
To simplify, divide both sides by the greatest common divisor, which is 4.
20 ÷ 4 = 5
144 ÷ 4 = 36
So, the simplified ratio is 5:36.
(d) 6 hours to a day
Ans: 1 : 4
A day consists of 24 hours.
So, the ratio is 6 to 24.
To simplify, divide both sides by the greatest common divisor, which is 6.
6 ÷ 6 = 1
24 ÷ 6 = 4
So, the simplified ratio is 1:4.
(e) 20 litres to 0.75 litres
Ans: 80 : 3
To express this ratio in simplest form, first, convert 0.75 liters to liters.
0.75 liters = 75/100 liters = 3/4 liters.
Now, the ratio becomes 20 liters to 3/4 liters.
To compare, we can convert 20 liters to 80/4 liters.
Now the ratio becomes 80/4 to 3/4.
To simplify, divide both sides by the greatest common divisor, which is 1/4.
(80/4) ÷ (1/4) = 80
(3/4) ÷ (1/4) = 3
So, the simplified ratio is 80:3.
(f) 1728 : 2400
Ans: 18 : 25
To express this ratio in simplest form, first, find the greatest common divisor of 1728 and 2400, which is 96.
Divide both sides by 96:
1728 ÷ 96 = 18
2400 ÷ 96 = 25
So, the simplified ratio is 18:25.
Q2: Simplify the following ratios.
(a) 1/4 : 1/6 : 1/8
Ans: 6 : 4 : 3
To simplify, find the least common denominator (LCD) which is 24.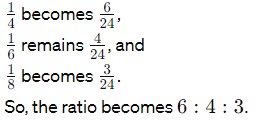
(b) 3.6 : 4.5
Ans: 4 : 5
To simplify, multiply each number by 10 to get rid of the decimals.
3.6 becomes 36,
4.5 becomes 45
So, the ratio becomes 36:45.
Then, divide both numbers by their greatest common divisor, which is 9.
36÷9=4 and 45÷9=5.
So, the simplified ratio is 4:5.
(c) 3²/₃ : 4¹/₂
Ans: 22 : 27
To simplify, convert each mixed number to an improper fraction.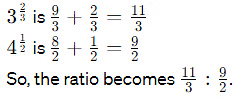
To make the denominators the same, multiply the first fraction's numerator and denominator by 2.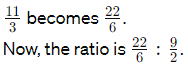
To simplify, find the least common denominator (LCD) which is 6.
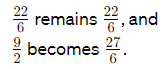
So, the ratio becomes 22:27.
(d) 3 : 2.4 : 2¹/₄
Ans: 20 : 16 : 15
To simplify, convert 2.4
2.4 to a fraction by multiplying numerator and denominator by 10.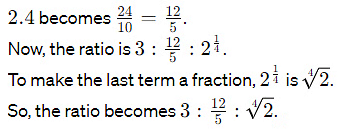
Q3: Determine if the following ratios form a proportion.
(a) 25 cm : 1 m = $40 : $160
(b) 200 ml : 2.5 l = $4 : $50
(c) 32 m : 64 m = 7 seconds : 14 seconds
(d) 6.5 litres : 13 litres = 50 kg : 10 kg
Ans: (a,b,c)
(a) 25 cm:1 m=40:160
Step 1: Convert all units to the same unit. 1 m=100 cm, so the ratio becomes 25 cm:100 cm=40:160.
Step 2: Check if the ratios are equal. 25×160=4000and 100×40=4000.
Since both products are equal, the ratios are proportional.
(b) 200 ml:2.5 l=4:50
Step 1: Convert all units to the same unit. 2.5 l=2500 ml, so the ratio becomes 200 ml:2500 ml=4:50
Step 2: Check if the ratios are equal. 200×50=10000 and 2500×4=10000.
Since both products are equal, the ratios are proportional.
(c) 32 m:64 m=7 seconds:14 seconds
Step 1: The units are already the same, so no conversion is needed.
Step 2: Check if the ratios are equal. 32×14=448 and 64×7=448.
Since both products are equal, the ratios are proportional.
(d) 6.5 litres:13 litres=50 kg:10 kg
Step 1: No conversion needed as the units are already the same.
Step 2: Check if the ratios are equal. 6.5×10=65 and 13×5=65.
Since both products are equal, the ratios are proportional.
So, for (a), (b), and (c), the ratios are in proportion. However, for (d), the ratios are not in proportion.
Q4: Divide 3000 among P, Q, R in the ratio 2 : 3 : 5
Ans: 600, 900, 1500
Divide 3000 among P, Q, R in the ratio 2 : 3 : 5
Step 1: Add up the parts of the ratio to find the total number of parts.
2+3+5=10
Step 2: Determine the share of each part.
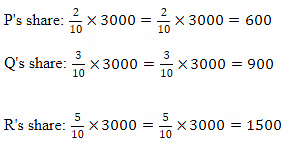
So, P gets 600, Q gets 900, and R gets 1500.
Q5: Which of the following statements are true?
(a) 25 : 35 = 45 : 55
Ans: False
To check if this is true, we find the cross-products:
25×55=1375 and
35×45=1575.
Since
1375≠1575, the statement is false.
(b) 105 : 30 = 49 : 14
Ans: True
To check if this is true, we find the cross-products:
105×14=1470 and 30×49=1470.
Since 1470=1470, the statement is true.
(c) 45 : 48 = 60 : 64
Ans: True
To check if this is true, we find the cross-products: 45×64=2880 and 48×60=2880.
Since 2880=2880, the statement is true.
(d) 2/3 : 7/9 = 3/4 : 5/6
Ans: False
To check if this is true, we find the cross-products: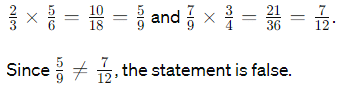
(e) 4.2 : 12.6 = 1.5 : 4.5
Ans: True
To check if this is true, we find the cross-products: 4.2×4.5=18.9 and 12.6×1.5=18.9.
Since 18.9=18.9, the statement is true.
(f) 12 : 18 = 28 : 12
Ans: False
To check if this is true, we find the cross-products: 12×12=144 and 18×28=504.
Since 144≠504, the statement is false.
So, the true statements are (b), (c), and (e).
|
56 videos|254 docs|40 tests
|
FAQs on Worksheet Solution: Ratio and Proportion - Mathematics for Class 5
| 1. What is the difference between ratio and proportion? |  |
| 2. How can ratios be simplified? |  |
| 3. How can proportions be solved? |  |
| 4. Can ratios and proportions be used in real-life situations? |  |
| 5. How can we determine if two ratios form a proportion? |  |





















