Chapter 13 - Proft, Loss, Discount and Value Added Tax (VAT) (Part -2), Class8 RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 13.26:
Question 1:
Find the S.P. if
(i) M.P. = Rs 1300 and Discount = 10%
(ii) M.P. = Rs 500 and Discount = 15%
ANSWER:
(i) We know that SP = MP−Discount
Discount% = Discount/MP × 100
Discount = 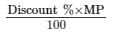
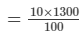
So, SP = Rs.(1300−(10/100 × 1300))
= 1300−130 = Rs. 1170
(ii) We know that SP = MP− Discount
Discount % = Discount/MP × 100
Discount = 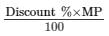
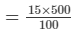
So, SP = Rs.( 500−(15/100 × 500)) = Rs.(500−75)
= Rs. 425
PAGE NO 13.26:
Question 2:
Find the M.P. if
(i) S.P. = Rs 1222 and Discount = 6%
(ii) S.P. = Rs 495 and Discount = 1%
ANSWER:
(i) Given, SP = Rs 1222
Discount = 6%
So, MP = 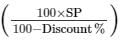
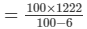
= Rs. 1300
(ii) Given,SP = Rs. 495
Discount = 1%
So, MP = 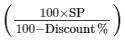
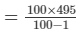
= Rs. 500
PAGE NO 13.26:
Question 3:
Find discount in percent when
(i) M.P. = Rs 900 and S.P. = Rs 873
(ii) M.P. = Rs 500 and S.P. = Rs 425
ANSWER:
(i) We know that SP = MP−Discount
So, 873 = 900−Discount
Therefore, Discount = Rs. (900−873)
= Rs. 27
Discount% = Discount/MP × 100%
= 27/900 × 100%
= 3%
(ii) We know that SP = MP−Discount
So, 425 = 500−Discount
Therefore, Discount = Rs.(500−425)
= Rs. 75
Discount% = Discount/MP × 100%
= 75/500 × 100%
= 15%
PAGE NO 13.26:
Question 4:
A shop selling sewing machines offers 3% discount on all cash purchases. What cash amount does a customer pay for a sewing machine the price of which is marked as Rs 650.
ANSWER:
Discount = 3%
Marked price = Rs. 650
Now, 3% of the MP = 3/100 × 650
= Rs 19.50
So, SP = MP−Discount = 650−19.50
= Rs 630.50
PAGE NO 13.26:
Question 5:
The marked price of a ceiling fan is Rs 720. During off season, it is sold for Rs 684. Determine the discount percent.
ANSWER:
Given, MP of the ceiling fan = Rs. 720 SP of the ceiling fan = Rs. 684
Since SP = MP−Discount,
Discount = MP−SP = Rs. (720−684)
= Rs. 36
Discount% = (Discount/MP) × 100%
= 36/720 × 100%
= 5%
PAGE NO 13.26:
Question 6:
On the eve of Gandhi Jayanti a saree is sold for Rs 720 after allowing 20% discount. What is its marked price?
ANSWER:
Given,SP of the saree = Rs. 720
Discount on the saree = 20%
We know, Discount% = Discount/MP × 100
Or, Discount = 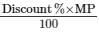
Let the MP of the saree be Rs. x
Therefore, Discount = 20/100 x = Rs. 0.02 x
Since S.P = MP− Discount,
720 = x −0.20 x 720 = 0.80 x
x = 720/0.80
= Rs. 900
Thus, the MP of the saree is Rs. 900.
PAGE NO 13.26:
Question 7:
After allowing a discount of 7.5% on the marked price, an article is sold for Rs 555. Find its markd price.
ANSWER:
Given,SP of the article = Rs. 555
Discount = 7.5%
Let the MP of the article be Rs. x .
Therefore, Discount = 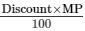 = Rs.7.5x/100
= Rs.7.5x/100
= Rs. 0.075 x
Since SP = MP− Discount,
555 = x −0.075 x
555 = 0.925 x
x = 555/0.925
= Rs. 600
Thus, the MP of the article is Rs. 600.
PAGE NO 13.26:
Question 8:
A shopkeeper allows his customers 10% off on the marked price of goods and still gets a profit of 25%. What is the actual cost to him of an article marked Rs 250?
ANSWER:
Let the CP of the article be Rs. x .
MP of the article = Rs. 250
Discount = 10%
Discount = 10% of 250 = 0.10 × 250 = Rs. 25
SP = MP−Discount = 250−25 = Rs. 225
Given,Profit = 25%
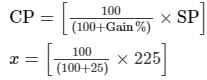
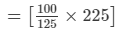
= Rs. 180
Thus, the CP of the article is Rs. 180.
PAGE NO 13.26:
Question 9:
A shopkeeper allows 20% off on the marked price of goods and still gets a profit of 25%. What is the actual cost to him of an article marked Rs 500?
ANSWER:
Given,MP of an article = Rs. 500
Discount = 20%
Therefore, Discount = 20% of 500
= 0.20 × 500
= 100
So, SP = MP−Discount
= Rs.(500−100)
= Rs. 400
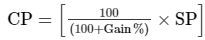
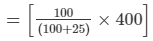
= 40000/125
= Rs. 320
Thus, the actual cost of the article is Rs. 320.
PAGE NO 13.26:
Question 10:
A tradesman marks his goods at such a price that after allowing a discount of 15%, he makes a profit of 20%. What is the marked price of an article whose cost price is Rs 170?
ANSWER:
Given,CP of the article = Rs. 170
Profit = 20%
We know that,
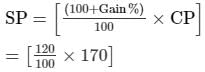
= 20400/100
= Rs. 204
Let the MP of the article be Rs. x .
Discount = 15%
Therefore, Discount = 15% of x = 0.15 x
So, SP = MP−Discount
MP = SP + Discount
x = 204 + 0.15 x
x −0.15 x = 204
0.85 x = 204
x = Rs. 240
Thus, the marked price of the article is Rs. 240.
PAGE NO 13.26:
Question 11:
A shopkeeper marks his goods in such a way that after allowing a discount of 25% on the marked price, he still makes a profit of 50%. Find the ratio of the C.P. to the M.P.
ANSWER:
Let C.P be Rs x and M.P be Rs y.
Gain% = 50
We know that,
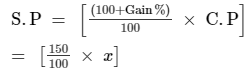
= 3/2 x
Discount% = 25
Discount = 25% of y
= Rs 0.25y
So, S.P = M.P − Discount
= y − 0.25y
= 0.75y
So, S.P = 0.75y
Also, S.P = 3/2 x
Comparing both values for S.P., we get:
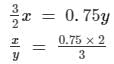
= 1.5/3
= 1/2
Thus, C.P:M.P = 1:2
PAGE NO 13.26:
Question 12:
A cycle dealer offers a discount of 10% and still makes a profit of 26%. What is the actual cost to him of a cycle whose marked price is Rs 840?
ANSWER:
Given, MP of the cycle = Rs. 840
Discount = 10%
So, SP = MP × 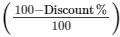
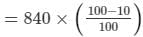
= Rs. 756
Now, SP = Rs. 756 and Gain = 26%
So, CP = 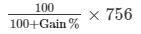
= 100/126 × 756
= Rs. 600
Hence, the actual cost of the cycle is Rs. 600.
PAGE NO 13.26:
Question 13:
A shopkeeper allows 23% commision on his advertised price and still makes a profit of 10%. If he gains Rs 56 on one item, find his advertised price.
ANSWER:
Let the CP of the item be Rs. x .
Profit = 10%
SP = CP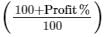
SP = x (110/100)
SP = Rs.1.1 x
Again, Profit = SP−CP
Therefore, Profit = Rs. (1.1 x − x ) = Rs. 0.1 x
We get,0.1 x = 56 x
= Rs. 560
Now, the advertised price = 1.1x /1−0.23
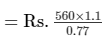
= Rs. 800
Therefore, the advertised price of the item is Rs. 800.
PAGE NO 13.26:
Question 14:
A shopkeeper marks his goods at 40% above the cost price but allows a discount of 5% for cash payment to his customers. What actual profit does he make, if he receives Rs 1064 after paying the discount?
ANSWER:
Let the original cost price of the item be Rs. x .MP = x + 40 x 100 = 1.4 x
Discount = MP−SP
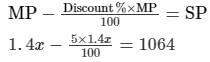
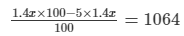
So, x (1.4)(0.95) = 1064
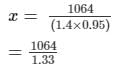
= Rs. 800
Profit = Rs. (1064−800)
= Rs. 264
Thus, the actual profit by the shopkeeper is Rs. 264.
PAGE NO 13.26:
Question 15:
By selling a pair of earings at a discount of 25% on the marked price, a jeweller makes a profit of 16%. If the profit is Rs 48, what is the cost price? What is the marked price and the price at which the pair was eventually bought?
ANSWER:
Let the cost price of the pair of earrings be Rs. x .
Profit = 16%
Therefore, SP =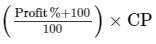
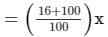
= Rs. 116x/100
SP−CP = 48
⇒ 116x/100− x = 48
⇒ 16 x = 4800
⇒ x = Rs. 300
SP = 116x/100 = Rs. 348
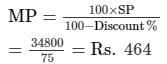
= Rs. 464
Thus, CP of the pair of earrings = Rs. x = Rs. 300
SP of the pair of earrings = Rs. 348
MP of the pair of earrings = Rs. 464
PAGE NO 13.26:
Question 16:
A publisher gives 32% discount on the printed price of a book to booksellers. What does a bookseller pay for a book whose printed price is Rs 275?
ANSWER:
Discount allowed by the publisher = 32% on the printed price
Printed price = Rs. 275
So, 32% of 275
= 32/100 × 275
= Rs. 88
So, the bookseller pays = Rs. 275−Rs. 88
= Rs. 187 for a book
PAGE NO 13.26:
Question 17:
After allowing a discount of 20% on the marked price of a lamp, a trader loses 10%. By what percentage is the marked price above the cost price?
ANSWER:
Let the CP of the lamp be Rs. 100.
Loss = 10% of CP = Rs. 10
So, SP = CP−Loss = Rs. 100−Rs. 10 = Rs. 90
The trader allows a discount of 20%. This means that when the MP is Rs. 100, the SP will be Rs. 80.
Now,If Rs. 80 is the SP, the MP = Rs. 100
If Re. 1 is the SP, the M.P = Rs. 100/80
If Rs. 90 is the SP, the MP = Rs. (100/80 × 90) = Rs. 112.50
Hence, the trader marks his goods at 12.5% above the cost price.
PAGE NO 13.26:
Question 18:
The list price of a table fan is Rs 480 and it is available to a retailer at 25% discount. For how much should a retailer sell it to gain 15%?
ANSWER:
Marked price of the table fan = Rs. 480
Discount = 25%
Therefore, cost price = 25% of Rs. 480
25/100 × 480 = Rs. 360
It is given that the profit on the table fan is 15%.
Gain% = Gain/CP × 100
15 = Gain/360 × 100
Gain = Rs. 54
Gain = SP−CP
54 = SP−360
SP = Rs. 414
Thus, the retailer will sell the table fan for Rs. 414.
PAGE NO 13.27:
Question 19:
Rohit buys an item at 25% discount on the marked price. He sells it for Rs 660, making a profit of 10%. What is the marked price of the item?
ANSWER:
Given,SP of the item = Rs. 660
Discount on the item = 25%
Profit on the item = 10%
We know,
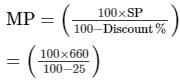
= Rs. 880
Thus, the marked price of the item is Rs. 880.
PAGE NO 13.27:
Question 20:
A cycle merchant allows 20% discount on the marked price of the cycles and still makes a profit of 20%. If he gains Rs 360 over the sale of one cycle, find the marked price of the cycle.
ANSWER:
Given,Gain on one cycle = Rs. 360
Gain = 20%
Gain% = Gain/CP × 100
20 = 360/CP × 100
CP = Rs. 1800
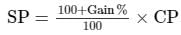
SP = 120/100 × 1800 = Rs. 2160
SP = Rs. 2160
Discount = 20%
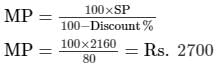
Hence, the MP of one cycle is Rs. 2700.
PAGE NO 13.27:
Question 21:
Jyoti and Meena run a ready-made garment shop. They mark the garments at such a price that even after allowing a discount of 12.5%, they make a profit of 10%. Find the marked price of a suit which costs them Rs 1470.
ANSWER:
Given,CP of the suit = Rs. 1470
Gain = 10%So, SP = Rs.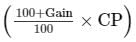
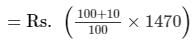
= Rs. 1617
Now,SP = Rs. 1617
Discount = 12.5%
So, MP = Rs. 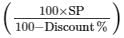
= Rs 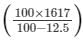
= Rs. 1848
Therefore, the marked price of the suit is Rs. 1848.
PAGE NO 13.27:
Question 22:
What price should Aslam mark on a pair of shoes which costs him Rs 1200 so as to gain 12% after allowing a discount of 16%?
ANSWER:
Given,CP of the pair of shoes = Rs. 1470
Gain = 12%
Discount = 16%
So, SP = Rs. 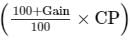
= Rs.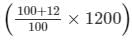
= Rs. 1344
Now,SP of the pair of shoes = Rs. 1344
Discount = 16%
So, MP = Rs. 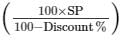
= Rs.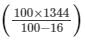
= Rs. 1600
Aslam should sell the pair of shoes for Rs. 1600.
PAGE NO 13.27:
Question 23:
Jasmine allows 4% discount on the marked price of her goods and still earns a profit of 20%. What is the cost price of a shirt for her marked at Rs 850?
ANSWER:
Given, MP of the shirt = Rs. 850
Discount = 4%
Discount allowed = Rs. (4100 × 850) = Rs. 34
Thus, SP of the shirt = Rs. (850−34) = Rs. 816
Now, Profit earned by Jasmine = 20%
Thus, CP = 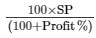
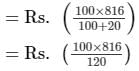
= Rs. 680
Thus, the cost price of the shirt is Rs. 680.Given,
PAGE NO 13.27:
Question 24:
A shopkeeper offers 10% off-season discount to the customers and still makes a profit of 26%. What is the cost price for the shopkeeper on a pair of shoes marked at Rs 1120?
ANSWER:
Given,MP of the pair of shoes = Rs. 1120
Discount = 10%
So, SP = MP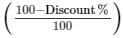
= 1120 × 90/100
= Rs. 1008
Now,Profit = 26%
SP = Rs. 1008
Therefore, CP = 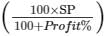
Cost price = 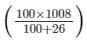
= Rs. 800
The cost price of the pair of shoes will be Rs. 800.
PAGE NO 13.27:
Question 25:
A lady shopkeeper allows her customers 10% discount on the marked price of the goods and still gets a profit of 25%. What is the cost price of a fan for her marked at Rs 1250?
ANSWER:
Given,MP of the fan = Rs. 1250
Discount = 10%
So, Discount = 10% of 1250 = 0.10 × 1250
= Rs. 125
Since SP = MP−Discount,
SP = Rs. (1250−125)
= Rs. 1125
Now, SP of the fan = Rs. 1125
Profit = 25%
CP =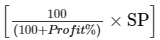
= [100/125]1125
= Rs. 900
Thus, the cost price of the fan is Rs. 900.
FAQs on Chapter 13 - Proft, Loss, Discount and Value Added Tax (VAT) (Part -2), Class8 RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What is the formula to calculate profit? |  |
| 2. How can I calculate the discount percentage? |  |
| 3. What is Value Added Tax (VAT)? |  |
| 4. How do I calculate the selling price after applying VAT? |  |
| 5. How can I calculate the loss percentage? |  |
















